Прямое произведение и проекция множеств

 

Упорядоченное множество называют кортежом (фр. cortege – торжественное шествие, выезд). Кортеж - последовательность элементов, в которой каждый элемент занимает определенное место. Элементы кортежа называются компонентами. Число элементов кортежа называется его длиной. Множество А=(а₁,а₂,…,а_n) является кортежом длины n с компонентами а₁,а₂,…,а_n. Понятие кортежа соответствует известному понятию вектора. Кортежи длины n называют n -ми, а пустой кортеж длины ноль обозначается () или L. В отличие от обычного множества в кортеже могут быть одинаковые элементы.

Кортеж длины три (а₁,а₂,а₃) рассматривается как точка в трехмерном пространстве (рис. 1.6), а его проекции на соответствующие плоскости образуют кортежи длины два (двойки) – (а₁,а₂), (а₁,а₃), (а₂,а₃), т.е.

Пр₁₂(а₁,а₂,а₃) = (а₁,а₂); Пр₁₃(а₁,а₂,а₃)=(а₁,а₃); Пр₂₃(а₁,а₂,а₃)=(а₂,а₃);

 

Рис. 1.6

Для n -мерного пространства проекция кортежа длины n на оси i, j,…, k определится как Пр_{i, j,…,k}(а₁,а₂,…,а_n)=(а_i,а_j,…,а_k), где 1 £ i < j <…< k £ n.

Прямым произведением множеств А и В является множество С (С=А´В), содержащее упорядоченные пары (двойки, кортежи длины два), первая компонента каждой из которых принадлежит множеству А, а вторая - множеству В. Прямое произведение множеств А и В запишется в виде выражения: С=А´В={(а, в)½аÎА, вÎВ}.

Истинно высказывание: (а, в)ÎА´В«аÎА & вÎВ. Например, дано А=(а₁, а₂, а₃) и В=(в₁, в₂), тогда С=А´В={(а₁,в₁),(а₁,в₂),(а₂,в₁),(а₂,в₂),(а₃,в₁),(а₃,в₂)}.

Подмножества множества С=А´В называют еще графиками.

Графиком называют любое множество, элементы которого представляют собой упорядоченные пары.

Если имеется n множеств А₁,А₂,…,А_n, то их прямым произведением называется множество С=А₁´А₂´…´А_n, состоящее из таких кортежей длины n, первая компонента каждого из которых принадлежит множеству А₁, вторая – множеству А₂,…, _n-я компонента принадлежит множеству А_n. Для произвольной _n-ки (а₁,а₂,…,а_n), принадлежащей прямому произведению множеств С=А₁´А₂´…´А_n, причем а₁ÎА₁, а₂ÎА₂,…, а_nÎА_n, истинно высказывание (а₁,а₂,…,а_n)ÎА₁´А₂´…´А_n«а₁ÎА₁, а₂ÎА₂,…, а_nÎА_n.

Если определить прямое произведение одного и того же множества А r раз, то мы получим множество С, которое явится r –й степенью множества А. Формально это будет записано в виде: С=А^r=А´А´…´А.

Определим также, что А₀={L}.

Пусть А – произвольное множество. Подмножество DАÍА² называется диагональю множества А, если оно состоит из пар вида (а,а), где аÎА. Если А=(а₁,а₂,а₃), то DА={(а₁,а₁), (а₂,а₂), (а₃,а₃)}.

Определим операцию проектирования множества. Пусть А – множество, состоящее из кортежей длины r. Тогда проекцией множества А будет называться множество проекций кортежей из множества А.

Рассмотрим пример. Пусть множество А состоит из трех троек

,

причем каждой тройке соответствует точка в трехмерном пространстве. Тогда проекции множества А на оси 1,2 и 3 определятся множествами Пр₁А= , Пр₂А= , Пр₃А= . Если обозначить Пр₁А=А₁, Пр₂А=А₂, Пр₃А=А₃, то очевидно, что А₁´А₂´А₃=А. Тогда, если С=А´В, то Пр1С=А, Пр2С=В, а если DÍА´В, то Пр1DÍА, Пр2DÍВ.

 

Соответствия

 

Если существует способ (закон) сопоставления элементов хÎХ с элементами yÎY так, что имеется возможность образования двоек (x,y), причем для каждого элемента хÎХ возможно указать элемент yÎY, с которым сопоставляется элемент х, то говорят, что между множествами Х и Y установлено соответствие. В сопоставлении могут участвовать не все элементы Х и Y. Для задания соответствия необходимо указать:

- множество Х, элементы которого сопоставляются с элементами другого множества;

- множество Y, с элементами которого сопоставляются элементы множества Х;

- множество QÍХ´Y, определяющее закон, согласно которому осуществляется соответствие, т.е. перечисляющее все пары (x,y), участвующие в сопоставлении.

Соответствие, обозначаемое через q, представляет собой тройку множеств q=(X,Y,Q), где: X – область отправления соответствия, Y – область прибытия соответствия, Q – график соответствия, QÍХ´Y. Очевидно, что Пр₁QÍХ, а Пр₂QÍY, причем множество Пр₁Q называется областью определения соответствия, а Пр₂Q – областью значений соответствия. Способы задания соответствий следующие.

При теоретико-множественном задании определяют множества Х={x₁, x₂,…, x_n}, Y={y₁, y₂,…,y_m} и график Q={(x_i,y_j)}, хÎХ, yÎY ,

При матричном способе задания соответствие задается в виде матрицы инцидентности R_Q, которая имеет вид прямоугольной таблицы размером n´m. Элементы хiÎХ соответствуют строкам матрицы R_Q, а элементы y_jÎY соответствуют столбцам. На пересечении х_i строки и y_j столбца ставится элемент r_ij=1, если элемент (x_i,y_j)ÎQ, и r_ij=0, если (xi,y_j)ÏQ.

При графическом способе соответствие задается в виде рисунка (см. рис. 1.7.), на котором элементы х_iÎХ – кружки одной линии, элементы y_jÎY – кружки другой линии, а каждая двойка (x_i,y_j)ÎQ обозначается стрелкой, идущей от кружка x_i к кружку y_j. Такое представление называется графиком.

Х={x₁,x₂,x₃,x₄}, Y={y₁,y₂,y₃}, Q={(x₁,y₁), (x₁,y₂), (x₂,y₁), (x₂,y₂), (x₃,y₂), (x₄,y₃)}.

Рис. 1.7

Если будем сопоставлять для множества элементов yÎY элементы из множества Х, то получим соответствие q^-1=(Y,X,Q^-1), обратное соответствие q (инверсия соответствия q).

Композиция (лат. compositio – сочинение, составление) соответствий - последовательное применение двух и более соответствий. Композиция двух соответствий есть операции с тремя множествами, на которых определены два соответствия:

Q=(X,Y,Q), QÍX´Y, p=(Y,Z,P), PÍY´Z.

Соответствие q определяет для некоторого элемента хÎХ некоторый (один или более) элемент yÎY, а соответствие p для некоторого элемента yÎY определяет некоторый элемент zÎZ. Композиция соответствий q(p) сопоставляет каждому элементу xÎX=Пр₁Q (области определения соответствия q) один или более элементов zÎZ=Пр₂P (области значений соответствия p). Композиция соответствий задается выражением q(p)=(X,Z,Q P).

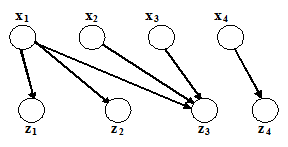
Пример графического задания композиции приведен на рис. 1.8 и рис. 1.9.

q={(x₁,x₂,x₃,x₄), (y₁,y₂), (x₁,y₁), (x₂, y₂), (x₃,y₂), (x₄,y₁)},

p={(y₁,y₂,y₃), (z₁,z₂,z₃,z₄), (y₁,z₁), (y₁,z₂), (y₁,z₄), (y₂,z₃), (y₃,z₃), (y₃,z₄)}

Рис. 1.8

q(p)={(x₁,x₂,x₃,x₄), (z₁,z₂,z₃,z₄), (x₁,z₁), (x₁,z₂), (x₁,z₄), (x₂,z₃), (x₃,z₃), (x₄,z₄)}

Рис. 1.9

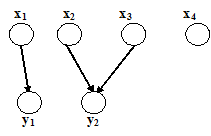
Пример графического задания операций объединения и пересечения соответствий приведен на рис. 1.10 – рис.1.12.

q={(x₁,x₂,x₃,x₄), (y₁,y₂,y₃), (x₁,y1), (x₁,y₂), (x₂,y₂), (x₂,y₃), (x₃,y₂), (x₄,y₃)}, p={(x₁,x₂,x₃,x₄), (y1,y₂), (x₁,y1), (x₂,y₂), (x₃,y₂), (x₄,y₁), (x₄, y₂)}.

Рис. 1.10

qÈp={(x₁,x₂,x₃,x₄), (y₁,y₂,y₃), (x₁,y₁), (x₁,y₂), (x₂,y₂), (x₂,y₃), (x₃,y₂), (x₄,y₁), (x₄,y₂), (x₄,y₃)}.

Рис. 1.11

 

qÇp={(x₁,x₂,x₃,x₄), (y1, y2), (x1, y1), (x2, y2), (x3, y2)}.

Рис. 1.12

 

Отображения

 

Для соответствия q=(X,Y,Г) ГÍX´Y, Пр₁ГÍX. Рассмотрим случай, когда Пр₁Г=X, т.е. тройка множеств (X,Y,Г) определяет соответствие, для которого область определения Пр₁Г совпадает с областью отправления Х. То есть для всякого хÎХ существует такой элемент yÎY, что двойка (х, y) ÎГ.

Соответствие, определенное на всяком хÎХ, называется отображением Х в Y и формально записывается в виде q=(X, Y, Г) или Г: Х®Y, где Г – закон, в соответствии, с которым осуществляется соответствие.

Если отображение неоднозначно, т.е. элементу хÎХ можно поставить в соответствие несколько элементов из множества Y, то в данном случае отображение Г элементу хÎХ ставит в соответствие некоторое подмножество Гх, причем ГхÍY, а Гх называется образом элемента х.

Пример: Пусть на экзамен явилось множество студентов S={s₁,s₂,…,s_n}. На экзамене каждому студенту может быть поставлена одна из множества оценок С={с₁,с₂,с₃,с₄}, где С={“неуд.”, “удовл.”, “хорошо”, “отлично”}.

Говоря языком теории множеств, (по закону Г – уровень знаний студентов) модель результатов экзамена будет представлена отображением (каждому элементу множества С сопоставляется элемент множества S) - Г: С®S.

Таким образом, каждой оценке С_i из множества С будут сопоставлены в соответствие некоторые подмножества студентов ГС₁, ГС₂, ГС₃, ГС₄, ГС_iÍS.

Пусть АÍХ. Образом ГА множества А называется совокупность элементов множества Y, которые являются образами Гх для всех хÎА.

В рассмотренном выше примере существует подмножество оценок П={с₂, с₃, с₄}, получив которые на экзамене, студент не считается задолжником по данному курсу. Тогда образом множества П будет множество ГПÍS, которое состоит из студентов, не имеющих к концу экзамена задолженности по данному курсу.

Рассмотрим свойства отображений.

Согласно сделанному выше определению, формально

.

Если А₁ и А₂ – подмножества Х, то образом множества, которое является объединением множества А1 и А₂, является объединение образов множеств А₁ и А₂. Формально это запишется в виде Г(А₁ÈА₂)=ГА₁ÈГА₂.

Если А₁ÍХ и А₂ÍХ, то образ множества, которое является пересечением множеств А₁ и А₂, входит в множество, являющееся пересечением образов множеств А₁ и А₂. Формально это можно записать в виде Г(А₁ÇА₂)ÍГА₁ÇГА₂. Если же отображение Г: Х®Y является однозначным, то Г(А₁ÇА₂)=ГА₁ÇГА₂. Очевидно, что если А₁ÍХ, А₂ÍХ,…, А_nÍХ, то

.

Для отображения имеет место понятие обратного отображения: q^-1=(Y, X, Г_-1) или Г^-1: Y®X, т.е. существует соответствие, при котором определяются элементы хÎХ, с которыми сопоставляются элементы yÎY. Аналогично существует понятие композиции отображений.

Рассмотрим случай, когда множества Х и Y совпадают, т.е. отображение Г: Х®Y есть отображение множества Х самого в себя и формально определяется парой (Х, Г), где ГÍХ² (ГÍХ´Х).

Пусть имеется два некоторых множества Г и D, каждое из которых есть отображение Х в Х, т.е. Г: Х®Х и D: Х®Х. Композиция этих отображений ГА будет иметь вид: (ГD)х=Г(Dх), или при Г=D получим Гх²=Г(Гх)=Г:Гх®Гх, т.е. Гх²ÍГх´ГхÍY.

Очевидно, что Гх³=Г(Гх²), Гх⁴=Г(Гх³) и т.д., т.е. при i³2 Гхⁱ=Г(Гх^i-1). Если ввести соотношение Гх⁰=х, т.е. отображение Г⁰ элементу хÎХ ставит в соответствие тот же элемент хÎХ, то и для i с отрицательным знаком имеем Гх⁰=Г(Г^х-1), Г^-i=Г^-1(Гх_i-1), когда i£-2. Отображения на одном множестве широко применяются в теории графов.

 

Отображение как функция

1.8.1. Функция. Отображение f: X®Y называется функцией, если оно является однозначным, т.е. для любых пар (x₁,y₁)Îf и (x₂,y₂)Îf, если х₁=х₂, следует y₁=y₂. Однозначное соответствие q=(X,Y,f) в этом случае называется функциональным, т.е. в графике f не может быть двух пар вида (x,y₁) и (x,y₂), y₁¹y₂, xÎX, y₁,y₂ÎY. Если существует такой элемент xÎX, образ которого содержит более одного элемента yÎY, то соответствие называется нефункциональным. Если же для любого элемента xÎX образ f(x) содержит более одного элемента yÎY, то соответствие называется антифункциональным. На рис. 1.13 приведены графические задания функционального, нефункционального и антифункционального соответствий.

*

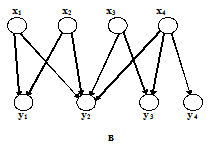
а – функциональное, б – нефункциональное, в – антифункциональное.

Рис. 1.13

 

Значение y в любой из пар (x,y)Îf называется функцией от данного х и записывается в виде логической формулы y=f(x). Формально функция определена: f={(x, y)ÎX´Y½y=f(x)}.

Говорят, что функция f отображает элемент xÎX в элемент yÎY; х – аргумент функции, y – значение функции на аргументе х; f – есть множество, элементами которого являются пары (x, y), участвующие в соответствии q=(X, Y, f).

Исходя из определения функции, рассмотрим способы ее задания. Если Х есть конечное множество небольшой мощности, то возможно задание функции перечислением всех пар (x, y), которые составляют множество f. Если Х и Y есть множество вещественных или комплексных чисел, то под f(x) понимается математическая формула. Например, если X=Y= - пространство действительных чисел, f={(x, y)β½y=x²}, то тогда f(x)=x².

Может рассматриваться случай, когда на некоторых Ai () подмножествах множества Х (A_iÍX, ) при определении соответствия в виде функции приходится пользоваться различными математическими формулами f_i(x), . Т.е. функция f(x) будет определена в виде

.

Например, релейная функция имеет вид

.

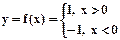Функция y=f(x)=½x½ задается в виде выражения

Множество пар (x,y)Îf можно также изобразить в виде точек на плоскости Â₂. В этом случае получим график функции. Если в выражении f: X®Y множество Х=U´V, то соответствие f: X®Y есть функция f(u,v) от двух переменных uÎU и vÎV, или формально записывается в виде

f={(u, v, y)ÎU´V´Y½y=f(u, v)}.

Можно определить в общем случае функцию от n числа переменных.

Существует операция сужения функции. Если f: X®Y – некоторая произвольная функция и АÍХ – произвольное множество, то сужением функции f на множестве А называется функция f_А, содержащая пары (x,y)Îf, в которых хÎА, а следовательно (x,y)ÎA´Y. Формально сужение функции определится выражением: f_A=fÇ(A´Y). Сужение функции возможно, например, при табличном задании функции, определенной на бесконечном множестве Х.

Так как соответствию q=(X,Y,Q) можно сопоставить обратное соответствие q^-1=(Y,X,Q^-1), то и функции f: X®Y можно сопоставить обратную функцию (отображение) f-1: Y®X. Условия получения обратной функции для отображения f: X®Y следующие. Отображение f: X®Y должно быть однозначным, т.е. для любых (x₁,y₁)Îf и (x₂,y₂)Îf из х₁=х₂ следует y₁=y₂. Отображение f: X®Y должно быть и взаимооднозначным, т.е. из условия х₁¹х₂ следует y₁¹y₂. При выполнении этих условий обратное отображение f^-1: Y®X также является однозначным и определяет функцию x=f^-1(y), называемую обратной по отношению к функции y=f(x).

1.8.2. Функция времени. Если в качестве множества Х функции взять множество моментов времени Т, а в качестве Y взять множество вещественных чисел Â, то получим отображение, называемое функцией времени f:T®Â. Время имеет одно направление, поэтому Т есть упорядоченное множество. Элементами функции являются двойки (t,x) или x(t), где tÎT, xÎÂ. Каждая такая пара задает значение функции в момент времени t и определяет мгновенное значение функции. Полная совокупность двоек (t,x) представляет собой функцию времени. Примером функции времени является синусоида: f={(t,x)ÎT´Â½ x=Asin(t+j)}.

Время является величиной бесконечной, поэтому на практике обычно рассматривают функцию, заданную на временных интервалах.

Сужение функции x(t), заданной на бесконечном интервале -¥<t<¥, на конечный интервал (t₁,t₂] называется отрезком функции x(t) и обозначается х(t₁,t₂], т.е. х(t₁,t₂]={x(t)½tÎ(t₁,t₂]}. Если множество Т представляет собой множество натуральных чисел, то функция f:T®Â называется функцией с дискретным временем. Элементы множества Т обозначаются через n (nÎT), так что двойка (n,x), обозначаемая также x[n] или x_n, определяет значение функции в момент n.

1.8.3. Функционал. Пусть в отображении f: X®Y множество Х есть множество функций F(x), а Y – множество вещественных чисел. В частности, пусть Y есть множество моментов времени. В этом случае приходим к отображению, называемому функционалом и формально записываемому выражением J: F(x)®T.

Понятие функционала поясним на примере. Известно, что если производить подключение питания к некоторой схеме, то в схеме протекают переходные процессы, определяемые параметрами схемы и поданным напряжением. На рис. 1.14 показан пример возможных протеканий переходного процесса. В зависимости от параметров функции f(x) время t установления переходного процесса различное.

Если множество функций f(x) обозначим через F(x), а через Т – множество вещественных чисел t, которые определяют время установления переходного режима, то зависимость времени протекания переходного режима записывается как отображение J: F(x)®T.

 

Рис. 1.14

Всевозможные пары (f(x),t) есть элементы множества J, причем f(x)ÎF(x), tÎT. Говорят, что вещественное число tÎT представляет собой функционал J от функции f(x)ÎF(x) или формально: t=J[f(x)].

В задачах теории автоматического регулирования определяется оптимальная функция f(x), которой соответствует минимальное время t установления переходного процесса для выходной величины. Требуется выполнить условие , при котором t будет минимальной величиной t_мин. Говоря языком теории множеств, необходимо сопоставить t_мин с некоторой функцией fi(x)ÎF(x).

1.8.4. Оператор. Если в отображении f: X®Y множества Х и Y являются множествами функций с элементами x(t)ÎX и y(t)ÎY, то данное отображение называется оператором и обозначается L: X®Y. Элементами множества L будут всевозможные пары (x(t),y(t)). Оператор L преобразует функцию x(t) в функцию y(t) и поэтому y(t)=L[x(t)]. В математике известны операторы:

- дифференцирования fⁱ(x)=P[f^i-1(x)], i³1, что имеет запись в математическом анализе fⁱ(x)=df^i-1(x)/dx;

- интегрирования f(x)=j(x)/p, что соотвествует записи ;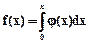

а также много других операторов.

В системах автоматического управления оператором преобразования управляющей величины x(t) в управляемую величину y(t) можно рассматривать передаточную функцию системы.

 

Отношения

 

1.9.1. Свойства отношений. Отношение j=(X, Г) - это отображение j=(X,Y,Г), X=Y, заданное на одном множестве Х, называемом областью задания отношения, график которого Г. Говорят, что элемент yÎГ(х), причем y=(x,x), yÎX находится в отношении Г (по закону Г) к элементу х и формально записывают yГх. Если отображение задано на одном множестве, то отношение есть пара множеств (X,Г), причем ГÍХ₂. Элементами множества Х₂ являются упорядоченные пары, следовательно, отношение есть множество упорядоченных пар. Так как каждая пара связывает между собой только два элемента множества Х₂, то такое отношение называют бинарным.

Если Х=Æ, то отношение называется пустым и обозначается в виде L. Два отношения j=(X, Г) и d=(Y, P) называются равными, если X=Y, а Г=Р. Отношения, как и соответствия, могут быть заданы тремя способами: теоретико-множественным, матричным и графическим.

При матричном способе задания матрица смежности представляет собой квадратную таблицу размера n´n (где n – мощность множества Х). Строки и столбцы матрицы помечены элементами x_iÎX, а на пересечении x_i строки и x_j столбца ставится элемент r_ij=1, если (x_i,x_j)ÎГ или r_ij=0, если (x_i,x_j)ÏГ.

При графическом способе задания отношение изображается графом, у которого элементы – произвольно расположенные точки на плоскости, есть вершины графа, а каждая двойка (x_i,x_j)ÎГ – есть дуга графа, направленная от вершины xi к вершине xj.

Например, пусть Х=(x₁,x₂,x₃,x₄), Г={(x₁,x₁), (x₁,x₂), (x₂,x₃), (x₂,x₁), (x₃,x₂), (x₃,x₃)}. Матрица смежности, задающая данное отношение, имеет следующий вид:

На рис. 1.15 приведено графическое задание данного отношения.

Если некоторые х₁,х₂ÎХ, то х₁Гх₂ является истинным или ложным высказыванием, в зависимости от того, истинно или ложно высказывание (x₁,x₂)ÎГ.

Пусть x,y,z – любые элементы из множества Х. Рассмотрим свойства отношений.

Рис. 1.15

 

Отношение (Х,Г) называется рефлексивным (лат. reflexio - отражение), если для любого хÎХ истинным является высказывание хГх.

Графически рефлексивное отношение задают в виде графа, у которого имеется петля у каждой вершины. Если рефлексивное отношение задается в виде матрицы смежности, то у данной матрицы все элементы по главной диагонали равны единице, т.е. r_ij=1, (), n – мощность множества Х.

Отношение (Х,Г) называется нерефлексивным, если для любого хÎХ истинным является высказывание . Для графа нерефлексивного отношения характерно отсутствие петли на одной из вершин. В главной диагонали матрицы смежности, задающей нерефлексивное отношение, хотя бы один элемент главной диагонали r_ij=0, ().

Нерефлексивное отношение является антирефлексивным, если истинно высказывание 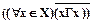. Для графа, задающего антирефлексивное отношение, характерно, что ни одна из вершин не имеет петлю, и, следовательно, в матрице смежности все элементы главной диагонали равны нулю.

На рис. 1.16 приведены графы, задающие соответственно рефлексивное, нерефлексивное и антирефлексивное отношения.

Отношение (Х,Г) называется симметричным (гр. symmetria - соразмерность), если истинно высказывание ("x,yÎX)(xГy®yГx). Если в графе симметричного отношения между какими-либо двумя вершинами x₁ и x₂ есть дуга, то обязательно должна быть дуга с противоположной ориентацией, а матрица смежности отношения симметрична относительно главной диагонали, т.е. если r_ij=1, то и r_ji=1, если r_ij=0, то и r_ji=0 ().

Отношение (Х,Г) называется несимметричным, если истинно высказывание ù (("x,yÎX)(xГy®yГx)). Граф несимметричного отношения отличается от графа симметричного отношения тем, что хотя бы одна пара вершин не имеет дуги с противоположной ориентацией.

Отношение (Х,Г) называется асимметричным, если истинно высказывание ("x,yÎX)(xГy®ùyГx). Граф асимметричного отношения не имеет петель и не имеет дуг с противоположной ориентацией, а в матрице смежности данного отношения r_ii=0 (), а если r_ij=1, то r_ji=0, или если r_ij=0, то и r_ji=1 для всех i¹j. Отметим, что любое асимметричное отношение является в то же время антирефлексивным.

 

Рис. 1.16

а – рефлексивное, б – нерефлексивное, в – антирефлексивное отношения.

 

Отношение (Х,Г) называется антисимметричным, если истинно высказывание ("x, yÎX)(xГy&x¹y)®ùyГx, или истинно высказывание, которое также определяет антисимметричность ("x,yÎX)(xГy&yГx)®x=y. Граф антисимметричного отношения отличается от графа асимметричного отношения тем, что он может содержать петли, т.е. хотя бы один элемент r_ii¹0 () в матрице смежности, а если r_ij=1, то r_ji=0, и наоборот для всех , i¹j. На рис. 1.17 приведено графическое задание соответственно симметричного, несимметричного, асимметричного и антисимметричного отношений.

Отношение (Х,Г) называется транзитивным, если истинно высказывание ("x,y,zÎX)(xГy&yГz®xГz), или в противном случае отношение (Х,Г) называется нетранзитивным. Граф транзитивного отношения отличается тем, что если для каких-либо трех вершин x_i,x_j,x_k имеются дуги, идущие из вершины xi в вершину x_j и из вершины x_j в вершину x_k, то обязательно должна быть дуга, идущая из вершины x_i в вершину x_k. В противном случае это будет граф нетранзитивного отношения. На рис. 1.18 представлена иллюстрация графов соответственно транзитивного и нетранзитивного отношений.

Рис. 1.17

а – симметричное, б – несимметричное, в – асимметричное,

г – антисимметричное отношения

 

Рис. 1.18

а – транзитивное, б – нетранзитивное отношения

 

Отношение (Х,Г) называется связанным, если истинно высказывание ("x,yÎX)(x¹y®xГyÈyГx). Если данное высказывание ложно, то отношение (Х, Г) называется несвязанным, а истинным является высказывание

ù(("x,yÎX)(x¹y®xГyÈyГx)).

На графе связанного отношения между любой парой вершин x_i и x_j () должна быть хотя бы одна дуга. На рис. 1.19 приведена иллюстрация связного и несвязного отношений.

Рис. 1.19

а – связное, б – несвязное отношения

 

1.9.2. Отношение эквивалентности. Для отношения эквивалентности (лат. aequus – равный + valens (valentis) - имеющий силу, значение, цену) должны выполняться три условия:

- каждый элемент хÎХ эквивалентен самому себе, т.е. отношение рефлексивно, следовательно, истинно высказывание ("хÎХ)(хГх);

- высказывание, что два элемента хÎХ и yÎХ являются эквивалентными, не требует уточнения, в какой последовательности рассматриваются элементы, т.е. отношение симметрично и истинно высказывание ("x,yÎX)(xГy®yГx);

- два элемента, эквивалентные третьему, эквивалентны между собой, т.е. отношение транзитивно и, следовательно, истинно высказывание

("x, y, zÎX)(xГy&yГz®xГz).

Если элементы множества при рассмотрениях могут быть заменены друг другом, то данные элементы находятся в отношении эквивалентности. Отношение эквивалентности находится в тесной связи с разбиением множеств. Пример отношений эквивалентности следующий. Отношение «быть в одной группе», заданное на множестве студентов.

Пусть J - некоторое множество индексов. Обозначим через {A_jÍX½jÎJ} множество классов эквивалентности для множества Х. Все элементы одного класса эквивалентности эквивалентны между собой (свойство транзитивности). Всякий элемент хÎХ может находиться в одном и только одном классе. Тогда Х является объединением непересекающихся множеств A_j, так что полная система классов {A_jÍX½jÎJ} является разбиением множества Х. Таким образом, каждому отношению эквивалентности на множестве Х соответствует некоторое разбиение множества Х на классы Aj.

Отношения эквивалентности на множестве Х и разбиение этого множества на классы A_jÎМ, где М – разбиение множества Х, называются сопряженными, если для любых хÎХ и yÎХ отношение хГy выполняется тогда и только тогда, когда х и y принадлежат одному и тому же классу A_j разбиения, т.е. должно быть истинно высказывание:

("х, yÎХ)[хГy®($АÎМ)(хÎА&yÎА)]

1.9.3. Отношение порядка. Можно упорядочить элементы множества Х или группы элементов, т.е. ввести отношение порядка на множестве Х. При этом, возможно, пользоваться понятиями «больше», «больше или равно», «меньше», «меньше или равно» с применением известных математических символов >, ³, <, £. Например, для элементов множества моментов времени Т t₁£t₂. Рассматривая стоимости различных предметов, как множество, мы можем расположить предметы в порядке возрастания стоимости. Различают отношения нестрогого порядка, для которых справедлив символ £, и отношения строгого порядка, для которых справедлив символ <.

Отношение (Х, Г) называется отношением нестрогого порядка, если оно:

- рефлексивно, т.е. истинно высказывание ("хÎХ)(хГх);

- антисимметрично, т.е. истинно высказывание ("x, yÎX) [xГy&yГx®x=y];

- транзитивно, т.е. истинно высказывание ("x, y, zÎX)(xГy&yГz®xГz).

Причем перечисленные выше свойства возможно также записать в виде: х£х – истинно (рефлексивность); х£y и y£x®x=y (антисимметричность); х£y и y£z®x£z (транзитивность).

Отношение (Х, Г) называется отно

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: