 |
Модель вычисления степени истинности нечетких правил вывода
|
|
|
|
Рассмотренная в разд. 4.1 модель классификации обладает трудностями применения, избежать которые можно путем ограничения числа рассматриваемых правил принятия решений об управлении.
Известна модель, названная в работе [7] моделью композиции, которая в работе [8] названа более полно моделью вычисления степени истинности нечетких правил вывода. Применение этой модели позволит избежать недостатка модели классификации, связанного с ростом числа строк таблицы соответствия «ситуация-действие».
Модель вычисления степени истинности нечетких правил вывода задается тройкой (X,T,H), где Т - нечеткое отношение на множестве X´H, причем Т - нечеткое соответствие, которое выводится на основе словесно - качественной информации экспертов:  Заметим, что в данной модели множества H рассматривается как множество НП из терм-множества ЛП - принимаемое решение. Формальное задание модели вычисления степени истинности нечетких правил вывода происходит следующим образом.
Заметим, что в данной модели множества H рассматривается как множество НП из терм-множества ЛП - принимаемое решение. Формальное задание модели вычисления степени истинности нечетких правил вывода происходит следующим образом.
Элементы множества X - множества, составляющего прямое произведение множеств входных факторов X=X1´X2´…´Xn, определяются при конкретной постановке задачи управления объектом. Определяется ЛП - принимаемое решение об управлениях и задаются элементы из терм-множества ЛП, характеризующие нечетко заданное принятие решения.
Основной частью построения модели является выбор экспертами элементов множества Т - соответствия в виде правил нечеткого выбора решения о кредитовании. Полнота этого множества определяет достоверность работы модели. Эксперт описывает принятия решений в виде некоторого множества Т, содержащего высказывания  . Высказывания pj формализуют посредством назначающих, условных и безусловных операторов. Для каждого высказывания pj выводится функция принадлежности
. Высказывания pj формализуют посредством назначающих, условных и безусловных операторов. Для каждого высказывания pj выводится функция принадлежности  Для отношения Т значения функции принадлежности определяются через обобщенную операцию s, так что
Для отношения Т значения функции принадлежности определяются через обобщенную операцию s, так что
|
|
|
 (4.3)
(4.3)
В результате модель вычисления степени истинности нечетких правил вывода будет иметь вид:
(X,T,H), X=X1´X2´…´Xn,  . (4.4)
. (4.4)
Построенная таким образом модель вычисления степени истинности нечетких правил вывода работает по следующему алгоритму при принятии решения о выборе управления.
Для момента времени t0 определяется координата множества X  , характеризующая состояние объекта управления в этот момент времени t0. Для точки x0 определяют значения функций принадлежности
, характеризующая состояние объекта управления в этот момент времени t0. Для точки x0 определяют значения функций принадлежности 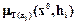 нечеткого решения выбора hi решения об управлении.
нечеткого решения выбора hi решения об управлении.
Затем выбирается такое значение базового множества (W в модели классификации) лингвистической переменной, качественно определяющей принимаемое решение, при котором значение функций принадлежности  имеет максимальное значение
имеет максимальное значение

Решение hi об управлении является выбранным в результате работы модели вычисления степени истинности нечетких правил вывода.
К числу достоинств данной модели следует отнести ее упрощенную реализацию по сравнению с моделью классификации, так как в данной модели не осуществляется экспертами перебор и анализ всех нечетких ситуаций, которые могут существовать при решении задачи управления. Эксперты формулируют правила вывода лишь для наиболее значимых, с их точками зрения, нечетких ситуаций, характеризующих объект управления, и соответствующих им нечетким решениям о параметрах управления.
Однако данная модель обладает и недостатками. Нет уверенности в том, что экспертами задано достаточно полное множество непротиворечивых правил, которые бы включали в себя все значимые нечеткие ситуации с требуемыми для этих ситуаций решениями о параметрах управления. Если же стремиться с перебору всех возможных правил принятия решений, то модель вычисления степени истинности нечетких правил вывода сводится к модели классификации.
|
|
|
Работу модели вычисления степени истинности нечетких правил вывода рассмотрим на примере устройства выбора корректирующей способности циклического кода [8].
Современные модемы построены, как адаптивные системы, имеющие канал обратной связи, с помощью которого осуществляется контроль состояний канала передачи дискретной информации (КПДИ). Система передачи информации (СПИ) подобного вида носит название системы с решающей обратной связью либо с информационной обратной связью. При искажении переданного кода, выявленного с применением канала обратной связи, происходит повторение передачи. Если применять циклический код с постоянной корректирующей способностью, то такие системы не будут эффективны. Их эффективность можно повысить, если применять коды различной корректирующей способности в зависимости от изменений уровня помех в КПДИ. Если B - скорость модуляции в канале, то для передачи N сообщений кодом наибольшей корректирующей способности (длина кода nk) потребуется время T=Nnk/B (с). Если применять коды различной корректирующей способности с длинами n1,n2,n3,…,nk, (n1<n2<n3<…<nk), то для передачи N сообщений потребуется время
 ,
,
где pi - финальная вероятность применения кода с длиной ni. Очевидно, что если для любого pi³0, то Ta<T.
Исходными данными для принятия решения о выборе корректирующего кода является текущее состояние КПДИ, характеризуемое действующим значением напряжения помехи в линии связи, числом переспросов о повторных передачах за заданный отрезок времени, скоростью модуляции в канале связи и другими факторами.
Пусть значение напряжения помехи будет определено в множестве X1, значение числа переспросов определено в множестве X2, значение числа скоростей модуляции в канале связи определено в множестве X3. Множество применяемых для передачи кодов упорядочено в соответствии с ростом длины кода K={n1,n2,n3,…,nk}.
Введем ЛП a - «уровень помех», терм-множество которой имеет вид T(a)= { a1, a2, a3, a4 }, где a1 - «несущественный уровень помех»; a2 - «низкий уровень помех»; a3 - «средний уровень помех»; a4 - «высокий уровень помех». Для каждой НП ai задаются нечеткие подмножества  где X1={0,x1max} - множество значений напряжения помехи, причем считается, что канал симметричный и помехи одинаково распределены по знаку. Вид функций принадлежности
где X1={0,x1max} - множество значений напряжения помехи, причем считается, что канал симметричный и помехи одинаково распределены по знаку. Вид функций принадлежности  приведен на рис. 4.8.
приведен на рис. 4.8.
|
|
|

Рис. 4.8
Введем ЛП b - «число переспросов», терм-множество которой имеет вид T(b)=(b1,b2,b3), где bi - НП: b1 - «небольшое число переспросов»; b2 - «обычное число переспросов»; b3 - «большое число переспросов». Зададим нечеткие подмножества  где X2={0,...,x2max} -множество значений число переспросов. Вид функций принадлежности
где X2={0,...,x2max} -множество значений число переспросов. Вид функций принадлежности  приведен на рис. 4.9.
приведен на рис. 4.9.

Рис. 4.9
Определим ЛП g - «скорость модуляции», терм-множество которой имеет вид T(g)= (g1,g2,g3), где g1 – «невысокая скорость модуляции»; g2 - «средняя скорость модуляции»; g3 – «большая скорость модуляции». Зададим нечеткие подмножества  . Вид функций принадлежности
. Вид функций принадлежности  приведен на рис. 4.10.
приведен на рис. 4.10.

Рис. 4.10
Определим ЛП d - «корректирующая способность кода», терм-множество которой имеет вид T(d)= (d1,d2,d3), где d1 – «небольшая корректирующая способность кода»; d2 - «средняя корректирующая способность кода»; d3 – «большая корректирующая способность кода». Зададим нечеткие подмножества  где K={n1,n2,n3,…,n10}. Вид функций принадлежности
где K={n1,n2,n3,…,n10}. Вид функций принадлежности 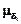 приведен на рис. 4.11.
приведен на рис. 4.11.

Рис. 4.11
Пусть экспертами представлены следующими правилами особенности функционирования системы управления выбором кода:
- p1: если a1 - несущественный уровень помех и b1 - небольшое число переспросов и g1 – невысокая скорость модуляции, то d1 - небольшая корректирующая способность кода;
- p2: если a1 - несущественный уровень помех и b2 - обычное число переспросов и g2 - средняя скорость модуляции, то d2 - средняя корректирующая способность кода;
- p3: если a1 - несущественный уровень помех и b2 - обычное число переспросов и g1 – невысокая скорость модуляции, то d1 - небольшая корректирующая способность кода;
- p4: если a1 - несущественный уровень помех и b2 - обычное число переспросов и g3 – большая скорость модуляции, то d2 - средняя корректирующая способность кода;
|
|
|
- p5: если a1 - несущественный уровень помех и b3 - большое число переспросов и g2 - средняя скорость модуляции, то d3 - большая корректирующая способность кода;
- p6: если a2 - низкий уровень помех и b1 - небольшое число переспросов и g2 - средняя скорость модуляции, то d1 - небольшая корректирующая способность кода;
- p7: если a2 - низкий уровень помех и b2 - обычное число переспросов и g2 - средняя скорость модуляции, то d2 - средняя корректирующая способность кода;
- p8: если a3 - средний уровень помех и b2 - обычное число переспросов и g3 - высокая скорость модуляции, то d2 - средняя корректирующая способность кода;
- p9: если a3 - средний уровень помех и b3 - большое число переспросов и g2 - средняя скорость модуляции, то d3 - большая корректирующая способность кода;
- p10: если a3 - средний уровень помех и b3 - большое число переспросов и g3 - высокая скорость модуляции, то d3 - большая корректирующая способность кода;
- p11: если a4 - высокий уровень помех и b2 - обычное число переспросов и g2 - средняя скорость модуляции, то d3 - большая корректирующая способность кода;
- p11: если a4 - высокий уровень помех и b3 - большое число переспросов и g3 - высокая скорость модуляции, то d3 - большая корректирующая способность кода.
Модель вычисления степени истинности нечетких правил вывода для данной задачи будет иметь вид
(X,T,К), X=X1´X1´X3´К,  .
.
Значение функции принадлежности нечеткого выбора управляющего решения определяется по формуле





 .
.
Для принятия решения о выборе корректирующей способности кода в момент времени t0 определяются значения x1(t0), x2(t0), x3(t0) и находится значение функции mT(x1(t0),x2(t0),x3(t0),n). Та величина n, которой соответствует наибольшее значение функции принадлежности mT(x1(t0),x2(t0),x3(t0),n), и будет длиной корректирующего кода, который следует применять в момент времени t0.
Пусть, например, к моменту времени t0 известно, что уровень помех x1=5В, среднее число переспросов x2=3, а скорость модуляции x3=600 бод.
Из рис. 4.8 определяем  (x1)=0,05;
(x1)=0,05;  (x1)=0,9;
(x1)=0,9;  (x1)=0,3;
(x1)=0,3;  (x1)=0. Из рис. 4.9 определяем
(x1)=0. Из рис. 4.9 определяем  (x2)=0,6;
(x2)=0,6; 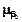 (x2)=0,5;
(x2)=0,5;  (x2)=0. Из рис. 4.10 определяем
(x2)=0. Из рис. 4.10 определяем 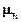 (x3)=1;
(x3)=1;  (x3)=0,05;
(x3)=0,05;  (x3)=0,1. Вычислим mT(x1(t0),x2(t0),x3(t0),n).
(x3)=0,1. Вычислим mT(x1(t0),x2(t0),x3(t0),n).
mT(x1(t0),x2(t0),x3(t0),n)=[0,05Ù0,6Ù1® 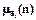 ]Ù[0,05Ù0,5Ù0,05®
]Ù[0,05Ù0,5Ù0,05®  ]Ù
]Ù
[0,05Ù0,5Ù1® 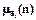 ]Ù[0,05Ù0,5Ù0,1®
]Ù[0,05Ù0,5Ù0,1®  ]Ù[0,05Ù0Ù0,05®
]Ù[0,05Ù0Ù0,05®  ]Ù
]Ù
[0,9Ù0,6Ù0,05® 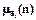 ]Ù[0,9Ù0,5Ù0,05®
]Ù[0,9Ù0,5Ù0,05®  ]Ù[0,3Ù0,5Ù0,1®
]Ù[0,3Ù0,5Ù0,1®  ]Ù
]Ù
[0,3Ù0Ù0,05®  ]Ù[0,3Ù0Ù0,1®
]Ù[0,3Ù0Ù0,1®  ]Ù[0Ù0,5Ù0,05®
]Ù[0Ù0,5Ù0,05®  ]=
]=
=[0,05® 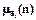 ]Ù[0,05®
]Ù[0,05®  ]Ù[0,05®
]Ù[0,05® 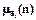 ]Ù[0,05®
]Ù[0,05®  ]Ù
]Ù
[0®  ]Ù[0,05®
]Ù[0,05® 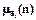 ]Ù[0,05®
]Ù[0,05®  ]Ù[0,1®
]Ù[0,1®  ]Ù
]Ù
[0®  ]Ù[0®
]Ù[0®  ]Ù[0®
]Ù[0®  ]=[0,95Ú
]=[0,95Ú 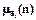 ]Ù[0,95Ú
]Ù[0,95Ú  ]Ù
]Ù
[0,95Ú 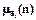 ]Ù[0,95Ú
]Ù[0,95Ú  ]Ù[1Ú
]Ù[1Ú  ]Ù[0,95Ú
]Ù[0,95Ú 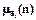 ]Ù[0,95Ú
]Ù[0,95Ú  ]Ù
]Ù
[0,9Ú  ]Ù[1Ú
]Ù[1Ú  ]Ù[1Ú
]Ù[1Ú  ]Ù[1Ú
]Ù[1Ú  ]=
]=
[0,95Ú 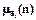 ]Ù[0,95Ú
]Ù[0,95Ú  ]Ù[1Ú
]Ù[1Ú  ]Ù[0,9Ú
]Ù[0,9Ú  ]=
]=
|
|
|
[0,95Ú 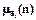 ]Ù[0,95Ú
]Ù[0,95Ú  ].
].
Таким образом, в сложившейся ситуации можно применить корректирующие коды с длинами от n5 до n10 (см. рис. 4.11).
|
|
|


