 |
Агрегация локальных выводов и дефазификация
|
|
|
|
Множество локальных выводов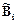 
, определенных правилами Ri, определяется в один общий вывод 
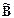операцией агрегации (aggregation). Общий вывод 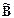характеризует базу правил 
.
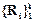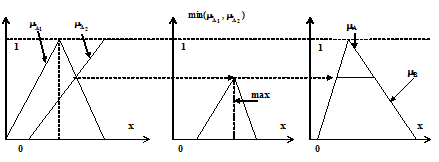
Рис. 3.11
Операция агрегации в символическом виде определена следующим образом:
Ri: если …, тогда 
(нечеткое множество 
известно) ®? нечеткое множество 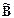для базы правил 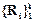, где символ ®? обозначает «найти».
Существуют несколько подходов к решению данной задачи [11]. Расмотрим два из них.
При первом подходе в экспертных системах вначале получают выводы по каждому из правил, а затем комбинируют эти выводы в общий вывод 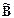, исходя из определенных алгоритмов.
При другом подходе вначале комбинируют все правила Ri, а затем получают вывод из этой комбинации, который принимается за общий вывод 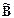для базы правил .
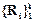Теория нечетких множеств позволила доказать, что при применении базиса Заде для вычисления операций нечетких «И», «ИЛИ» и нечеткой импликации эти два подхода при получении общего вывода дают эквивалентные результаты:
,
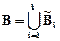где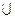 
- объединение локальных выводов в виде нечетких множеств .
Для характеристики процесса обработки на ЭВМ нечеткой информации принята единица быстродействия – FLIPS (число нечетких локальных выводов/сек). В настоящее время созданы нечеткие контроллеры с быстродействием 4.107 FLIPS.
Рассмотрим пример получения общего вывода 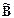на основе локальных выводов 
, 
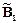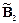
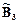. На рис. 3.12 показан процесс получения вывода .
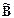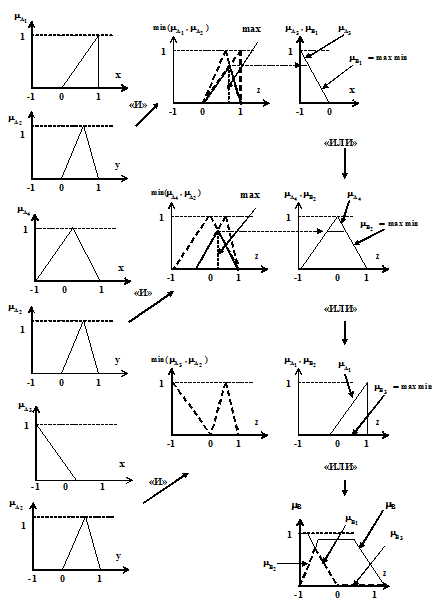
Рис. 3.12
База правил 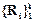содержит всего три правила:
R1: если x= 
и y= 
, тогда z=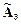 
;
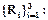R2: если x= 
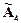и y= , тогда z= ;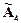
R3: если x= 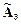и y= , тогда z= ,
где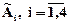 
- нечеткие множества, заданные своими функциями принадлежности. Нечеткие логические операции «И» и «ИЛИ» заданы по Заде. Функции принадлежности выводов определятся по формулам:
|
|
|
,
,
.
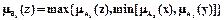Функция принадлежности общего вывода 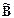определится формулой
.
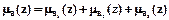Необходимо преобразовать результат нечеткого общего вывода 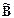в физическую переменную. Это происходит с применением операции дефазификации (defuuzzification – dfz).Для выполнения операции dfz применяют различные методы. Рассмотрим некоторые из них.
Преобразование общего вывода 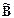в физическую переменную может быть сделано с помощью техники усреднения функции принадлежности mB(z) с применением метода центра тяжести (center of gravity - cog) на основе формул:
- аналоговое задание mB(z),
- дискретное задание mB(z),
где N – число разбиений при дискретизации функции принадлежности mB(z).
Метод центра тяжести cog при задании функции принадлежности mB(z1,z2,…, zn) в n –мерном пространстве позволяет определить численное значение i –й координаты по формуле:
,
где Z – произведение пространств.
На рис. 3.13 приведен пример дефазификации методом cog функции принадлежности mB(z), полученной в вышеприведенном примере (см. рис. 3.12).
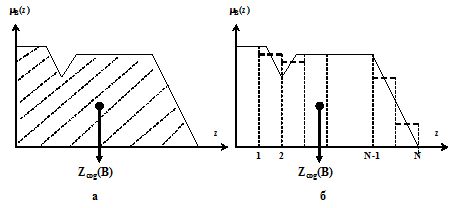Рис. 3.13
а – непрерывный cog; б – дискретный cog.
Достаточно широко распространен такой метод дефазификации, как метод центра области (center of area - coa), называемый еще методом медиана. Площадь под функцией принадлежности mB(z) разбивается на две равные части, так что:
.
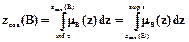Метод медианы показан на рис. 3.14.
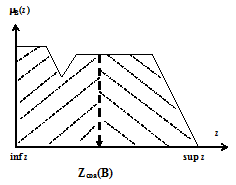
Рис. 3.14
Метод медианы может быть обобщен при задании функции принадлежности mB(z1,z2,…, zn) в n –мерном пространстве. Например, для двухмерного задания функции принадлежности mB(z1,z2) определение zcoa(B) происходит по формулам:
,
.
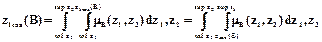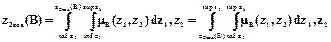Существует метод среднего максимума (mean of maxima - mom), для которого операция дефазификации выполняется, исходя из сечения множества 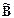при a=hgt 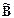. При этом результат определяется по формуле
,
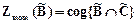где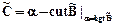 
- сечение множества 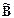при a=hgt 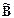. На рис. 3.15 показано применение метода mom.
Рис. 3.15
|
|
|
Так как метод mom «теряет» часть информации нечеткого множества 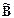, то этот метод применяется только в тех случаях, когда операция дефазификации имеет фильтрующие свойства. В данных случаях метод называют индексным или методом пороговой дефазификации (idexed defuzzification - idfz). В сочетании с методом cog его обозначают - icog. Результат дефазификации формально определен в виде
.
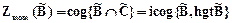В сочетании с методом coa метод пороговой дефазификации обозначают icoa. Результат дефазификации формально определен в виде
.
Существуют индексные методы с фильтрующими свойствами, в которых a=bt, bt - заданные априори значения (как правило, bt =0,5), а результат дефазификации определен в виде
,
.
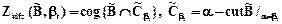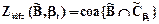На рис. 3.16 показана дефазификации индексными методами с уровнем разреза bt.
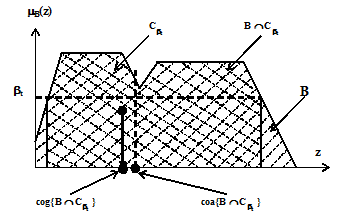
Рис. 3.16
При разработке систем управления в виде нечетких контроллеров могут применяться различные методы дефазификации в зависимости от поставленной задачи.
МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
|
|
|
