Нечеткие предикаты и кванторы

Нечеткие логические формулы могут быть определены не только на нечетких высказывательных переменных, но и на каком-либо множестве X. Эти формулы принимают свое значение также в отрезке чисел [0,1].

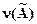Нечеткими предикатами называются нечеткие логические формулы, определенные на элементах множества X и принимающие значения внутри отрезка чисел [0,1]. Числовой характеристикой нечеткого предиката являются величины и . Величина , определяемая выражением =m_A(x₁)Ùm_A(x₂)Ù…Ùm_A(x_n), x_iÎX, 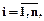называется степенью общности свойства для элементов множества X.

На нечеткую логическую формулу при значении 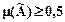может быть навешен квантор нечеткой общности 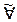, который имеет смысл «для любого» или «для всех». Величина 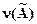, определяемая выражением 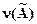=m_A(x₁)Úm_A(x₂)Ú…Úm_A(x_n), x_iÎX, 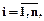называется степенью существования свойства для элементов множества X.

Если величина 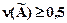, то на нечеткую логическую формулу может быть навешен квантор нечеткого существования , который читается «существует такой» или «имеется такой».

Возможно задание нечеткой логической формулы от одной переменной x, принимающей значения из множества X. Тогда выражение 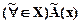является нечетко истинной формулой и читается «для любого xÎX степень истинности больше или равна 0,5».

Выражение является также нечетко истинной формулой и читается «существует такой xÎX, что степень истинности высказывания больше или равна 0,5».

Нечеткие высказывания

Нечетким высказыванием называется предложение, относительно которого можно судить о степени его истинности или ложности при данных входных переменных. Степень истинности (степень логичности) нечеткого высказывания принимает значения из замкнутого интервала [0,1]. Значения степени истинности 0 и 1 совпадают с понятиями лжи и истинности булевой алгебры логики. Нечеткое высказывание, степень истинности которого равна 0,5, называется индифферентностью. Примером нечеткого высказывания является: «скорость движения небольшая». Нечеткие высказывания делятся на простые и составные, которые образуются из простых с помощью логических операций отрицания, импликации, конъюнкции, дизъюнкции и т.д.

Отрицанием нечеткого высказывания называется нечеткое высказывание, обозначаемое ù , степень истинности которого определятется выражением ù =1- . Конъюнкцией нечетких высказываний и называется нечеткое высказывание, обозначаемое & , степень истинности которого определяется выражением & = 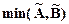. Логические операции здесь и далее имеют минимаксную трактовку логических операций, введенную Л.Заде [6].

Дизъюнкцией нечетких высказываний и называется нечеткое высказывание 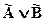, степень истинности определяется выражением

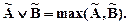
Импликацией нечетких высказываний и называется нечеткое высказывание, обозначаемое 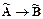, степень истинности которого определяется выражением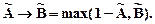

Эквивалентностью нечетких высказываний и называется нечеткое высказывание, обозначаемое 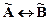, степень истинности которого находится выражением 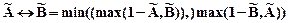. Высказывания и называются нечетко близкими, если степень истинности высказывания 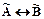больше значения 0,5, а при равенстве 0,5 - называют взаимно нечетко индифферентными.

Порядок выполнения логических операций в составном нечетком высказывании определяется скобками, а при их отсутствии сначала выполняются отрицания, затем конъюнкции, далее дизъюнкции, а после этого импликация и эквивалентность.