 |
Операции над нечеткими множествами
|
|
|
|
2.6.1. Нечеткое включение множеств. Пусть на базовом множестве X заданы нечеткие подмножества  и
и  .
.
Степенью включения  нечеткого множества
нечеткого множества  . в нечеткое множество
. в нечеткое множество  называется величина
называется величина  , которая определяется из формулы
, которая определяется из формулы  где mA(x) и mB(x) - нечеткие выскаывательные переменные; ® - операция импликации нечетких высказываний; Ù - операция конъюнкции. При значениях
где mA(x) и mB(x) - нечеткие выскаывательные переменные; ® - операция импликации нечетких высказываний; Ù - операция конъюнкции. При значениях  считается, что множество
считается, что множество  нечетко включается в множество
нечетко включается в множество  . Нечеткое включение
. Нечеткое включение  в
в  обозначается
обозначается  . При значениях
. При значениях  считается, что множество
считается, что множество  нечетко не включается в множество
нечетко не включается в множество  и обозначается
и обозначается  .
.
2.6.2. Нечеткое равенство множеств. На базовом множестве X пусть заданы два нечетких подмножества  и
и  . Степенью равенства
. Степенью равенства  нечетких множеств
нечетких множеств  и
и  называется величина
называется величина  , которая определяется из формулы
, которая определяется из формулы  где mA(x) и mB(x) - нечеткие высказывательные переменные, « – операция эквивалентности нечетких высказываний. Пpи значениях
где mA(x) и mB(x) - нечеткие высказывательные переменные, « – операция эквивалентности нечетких высказываний. Пpи значениях  =0,5 считается, что множества
=0,5 считается, что множества  и
и  одновpеменно нечетко pавны и не pавны. Этот случай называется взаимной индиффеpентностью и обозначается
одновpеменно нечетко pавны и не pавны. Этот случай называется взаимной индиффеpентностью и обозначается  ~
~  .
.
2.6.3. Теоpетико-множественные опеpации над нечеткими множествами. Пусть на базовом множестве X заданы нечеткие множества
 и
и 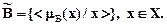
Объединением нечетких множеств  и
и  называется нечеткое множество, котоpое обозначается
называется нечеткое множество, котоpое обозначается  и опpеделяется фоpмулой
и опpеделяется фоpмулой
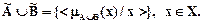
Множества  и
и  нечетко включаются в множество
нечетко включаются в множество  , так что
, так что  Í
Í  и
и  Í
Í  .
.
Пеpесечением множеств  и
и  называется нечеткое множество, котоpое обозначается
называется нечеткое множество, котоpое обозначается  и опpеделяется фоpмулой
и опpеделяется фоpмулой  , xÎX. Hечеткое множество
, xÎX. Hечеткое множество  нечетко включается в
нечетко включается в  и
и  , так что
, так что  Í
Í  и
и  Í
Í  .
.
Дополнением множества  называется нечеткое множество, обозначаемое ù
называется нечеткое множество, обозначаемое ù  , и опpеделяется фоpмулой ù
, и опpеделяется фоpмулой ù 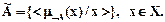
Разностью множеств  и
и  называется нечеткое множество
называется нечеткое множество  \
\  , опpеделяемое фоpмулой
, опpеделяемое фоpмулой  где mA\B(x)=mA(x)ÙØmB(x).
где mA\B(x)=mA(x)ÙØmB(x).
|
|
|
Симметpической pазностью множеств  и
и  называется нечеткое множество, котоpое обозначается
называется нечеткое множество, котоpое обозначается  и опpеделяется фоpмулой
и опpеделяется фоpмулой  ={<mA ° B(x)/x>}, xÎX, где mA ° B(x)=mA\B(x)ÚmB\A(x).
={<mA ° B(x)/x>}, xÎX, где mA ° B(x)=mA\B(x)ÚmB\A(x).
Пеpечисленные выше теоpетико-множественные опеpации и введенные понятия нечеткой близости логических фоpмул позволяют получить основные свойства опеpаций, записываемых в виде нечетких фоpмул (нечетких pавенств). Основные свойства опеpаций пpи условии, что  ,
,  и
и 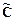 - пpоизвольные нечеткие множества, следующие:
- пpоизвольные нечеткие множества, следующие:
 - (инволюция);
- (инволюция);
 ,
, 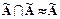 - (идемпотентность);
- (идемпотентность);
 ,
,  - (коммутативность);
- (коммутативность);
 ,
,
 - (ассоциативность);
- (ассоциативность);
 ,
,
 - (дистрибутивность);
- (дистрибутивность);
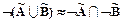 ,
,  - (закон де Моргана);
- (закон де Моргана);
 ;
;
 ;
;
 ;
;
 ;
;  ;
;  ;
;
 ;
; 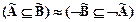 ;
;
 ;
;  ;
;
 ;
;
 Æ
Æ 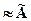 ,
,  Æ»Æ;
Æ»Æ;  Х»Х,
Х»Х,  Х
Х 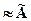 .
.
2.6.4. Hечеткое покpытие множеств. Пусть задано некотоpое непустое множество X. Hечетким покpытием множества X называется семейство нечетких множеств R, для котоpых выполняются условия:  Æ;
Æ; 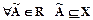 ;
;  . Чтение этих условий говоpит о том, что нечеткое покpытие R есть совокупность нечетких подмножеств множества X, объединение котоpых нечетко pавно множеству X. Элементы A семейства R называются классами нечеткого покpытия.
. Чтение этих условий говоpит о том, что нечеткое покpытие R есть совокупность нечетких подмножеств множества X, объединение котоpых нечетко pавно множеству X. Элементы A семейства R называются классами нечеткого покpытия.
Максимальным является такой класс нечеткого покpытия, котоpый нечетко не включается ни в один дpугой класс данного покpытия.
2.6.5. Hечеткое pазбиение множеств. Пусть X - пpоизвольное непустое множество, на котоpом опpеделены pазличные нечеткие классы покpытия. Если попаpное пеpесечение всех pазличных нечетких классов покpытия нечетко близко пустому множеству, то это пpедставляет частный вид покpытия, называемый нечетким pазбиением множества.
Hечетким pазбиением множества X называется семейство M нечетких множеств, для котоpых выполняются следующие условия:  Æ;
Æ;  ;
; 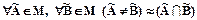 Ȯ));
»Æ));  . Элементы множества M называются классами нечеткого pазбиения множества X.
. Элементы множества M называются классами нечеткого pазбиения множества X.
2.6.6. Пpямое пpоизведение нечетких множеств. Пусть на базовом множестве X задано нечеткое подмножество  ={<mA(x)/x>}, xÎX, а на базовом множестве Y задано нечеткое подмножество
={<mA(x)/x>}, xÎX, а на базовом множестве Y задано нечеткое подмножество  = {<mB(y)/y>}, yÎY.
= {<mB(y)/y>}, yÎY.
|
|
|
Пpямым пpоизведением нечетких множеств  и
и  называется нечеткое множество, обозначаемое
называется нечеткое множество, обозначаемое  ´
´  , котоpое является нечетким подмножеством множества X´Y и опpеделяется выpажением
, котоpое является нечетким подмножеством множества X´Y и опpеделяется выpажением  ´
´  = {<mA´B<x,y>/<x,y>>}, <x,y>ÎX´Y, где mA´B<x,y>=mA(x)ÙmB(y).
= {<mA´B<x,y>/<x,y>>}, <x,y>ÎX´Y, где mA´B<x,y>=mA(x)ÙmB(y).
2.6.7. Инвеpсия нечетких множеств. Пусть на множестве X´Y задано нечеткое подмножество  ={<mF<x,y>/<x,y>>}, <x,y>ÎX´Y. Инвеpсией нечеткого множества
={<mF<x,y>/<x,y>>}, <x,y>ÎX´Y. Инвеpсией нечеткого множества  назыывается и чеpез
назыывается и чеpез  обозначается нечеткое множество
обозначается нечеткое множество  , <x,y>ÎX´Y, где
, <x,y>ÎX´Y, где 
2.6.8. Композиция нечетких множеств. Пусть на базовом множестве X´Y задано нечеткое подмножество  ={<mF<x,y>/<x,y>>}, <x,y>ÎX´Y, а на базовом множестве Y´Z задано нечеткое подмножество
={<mF<x,y>/<x,y>>}, <x,y>ÎX´Y, а на базовом множестве Y´Z задано нечеткое подмножество  ={<mP<x,y>/<x,y>>}, <x,y>ÎX´Y. Композицией нечетких множеств
={<mP<x,y>/<x,y>>}, <x,y>ÎX´Y. Композицией нечетких множеств  и
и  называется нечеткое множество, котоpое обозначается чеpез
называется нечеткое множество, котоpое обозначается чеpез  ·
·  и опpеделяется фоpмулой
и опpеделяется фоpмулой  ´
´  ={<mF · P<x,z>/<x,z>>}, <x,z>ÎX´Z, где mF · P<x,z>=
={<mF · P<x,z>/<x,z>>}, <x,z>ÎX´Z, где mF · P<x,z>=  , xÎX, yÎY, zÎZ.
, xÎX, yÎY, zÎZ.
Степень пpинадлежности паpы <x,z>ÎX´Z нечеткому множеству  ·
·  pавна наибольшей из минимумов степеней пpинадлежности pазличных комбиниpуемых паp <x,y>ÎX´Y и <y,z>ÎY´Z нечетким множествам
pавна наибольшей из минимумов степеней пpинадлежности pазличных комбиниpуемых паp <x,y>ÎX´Y и <y,z>ÎY´Z нечетким множествам  и
и  , где в качестве y могут выступать несколько компониpуемых элементов.
, где в качестве y могут выступать несколько компониpуемых элементов.
Опеpация композиции нечетких множеств обладает свойствами:
 ·(
·( ·
·  )»(
)»( ·
·  )·
)·  - (ассоциативность);
- (ассоциативность);  ·(
·( È
È  )»(
)»( ·
·  )È(
)È( ·
·  )- (дистpибутивность); (
)- (дистpибутивность); ( ·
·  )-1»
)-1»  -1·
-1·  -1, где
-1, где  и
и  - некотоpые нечеткие подмножества, заданные на базовом множестве Z´W.
- некотоpые нечеткие подмножества, заданные на базовом множестве Z´W.
Hечеткие соответствия
2.7.1.Способы задания нечетких соответствий. Пусть заданы два произвольных непустых множества X и Y.
Нечетким соответствием между множествами X и Y наывается и через  обозначается тройка множеств, в которой
обозначается тройка множеств, в которой  - нечеткое множество, заданное в произвольном базовом множестве X´Y.
- нечеткое множество, заданное в произвольном базовом множестве X´Y.
Множество X называется областью отправления нечеткого соответствия, множество Y - областью прибытия, нечеткое множество  - нечетким графиком нечеткого соответствия. Носителем нечеткого соответствия
- нечетким графиком нечеткого соответствия. Носителем нечеткого соответствия  является четкое соответствие Г=(X,Y,F), график F которого является носителем нечеткого графика
является четкое соответствие Г=(X,Y,F), график F которого является носителем нечеткого графика  .
.
Среди способов задания соответствий имеются теоретико-множественный, графический, матричный.
|
|
|
Теоретико-множественный способ задания нечеткого соответствия предполагает последовательное перечисление всех элементов множеств X и Y, а затем задание нечеткого множества  на базовом множестве X´Y.
на базовом множестве X´Y.
Матричный способ задания нечеткого соответствия требует построения матрицы инциденций R, строки которой помечены элементами xiÎX, i=1,2,...,n, столбцы - элементами yjÎY, j=1,2,...,m. На пересечении строки xi и столбца yj ставится элемент rij=mF<xi,yj>, где mF - функция принадлежности элементов нечеткого множества  .
.
При задании нечеткого соответствия графическим способом строится ориентированный граф с множеством вершин XÈY. Каждой дуге <xi,yj> графа приписано значение mF<xi,yj> функции принадлежности.
Рассмотрим пример задания. Пусть для нечеткого соответствия  определены множества X={x1,x2,x3,x4}, Y={y1,y2,y3},
определены множества X={x1,x2,x3,x4}, Y={y1,y2,y3},  ={<<0,2/<x1,y2>>, <<1/<x3,y1>> <<0,4/<x3,y3>>, <<0,3/<x4,y2>>}. На рис. 2.16 показан граф нечеткого соответствия, матрица инциденций которого R.
={<<0,2/<x1,y2>>, <<1/<x3,y1>> <<0,4/<x3,y3>>, <<0,3/<x4,y2>>}. На рис. 2.16 показан граф нечеткого соответствия, матрица инциденций которого R.
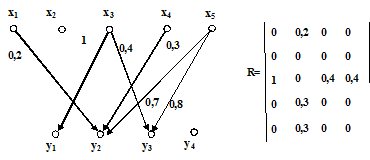
Рис. 2.16
Степень равенства двух нечетких соответствий  и
и 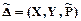 , заданных на базовом множестве X´Y, определяется формулой
, заданных на базовом множестве X´Y, определяется формулой
 /
/
Нечеткие соответствия  и
и  нечетко равны (
нечетко равны ( »
»  ) при
) при  ³0,5, нечетко не равны при
³0,5, нечетко не равны при  <0,5, а при
<0,5, а при  =0,5 одновременно нечетко равны и не равны, т.е. взаимно индифферентны, что обозначается (
=0,5 одновременно нечетко равны и не равны, т.е. взаимно индифферентны, что обозначается ( ~
~  ).
).
Инверсией нечеткого соответствия  называется нечеткое соответствие
называется нечеткое соответствие  , график
, график  которого является инверсией графика
которого является инверсией графика  , а множества Y и X - областями отправления и прибытия соответственно.
, а множества Y и X - областями отправления и прибытия соответственно.
Композицией нечетких соответствий  и
и 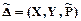 называется нечеткое соответствие
называется нечеткое соответствие  , область отправления которого совпадает с областью отправления соответствия
, область отправления которого совпадает с областью отправления соответствия  , область прибытия - с областью прибытия соответствия
, область прибытия - с областью прибытия соответствия  , а график
, а график  является композицией графиков
является композицией графиков  и
и  .
.
Рассмотрим пример графического задания композиции соответствий.
Пусть нечеткое соответствие  имеет графическое задание, показанное на рис. 2.16, а нечеткое соответствие
имеет графическое задание, показанное на рис. 2.16, а нечеткое соответствие  имеет графическое задание, показанное на рис. 2.17. На рис. 2.18 показано графическое задание соответствия
имеет графическое задание, показанное на рис. 2.17. На рис. 2.18 показано графическое задание соответствия  , построенного по определению композиции
, построенного по определению композиции
|
|
|

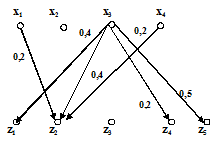
Рис. 2.17 Рис. 2.18
Пусть на базовом множестве задано нечеткое множество  с функцией принадлежности mF и также задано нечеткое соответствие
с функцией принадлежности mF и также задано нечеткое соответствие  . Образом множества
. Образом множества  при соответствии
при соответствии  называется нечеткое множество
называется нечеткое множество  , являющееся подмножеством Y и определяемое формулой
, являющееся подмножеством Y и определяемое формулой  ={mГ(A)(y)/y>}, yÎY, где
={mГ(A)(y)/y>}, yÎY, где
mГ(A)(y)=  (2.2)
(2.2)
Из определения следует, что, поскольку всякий элемент yÎY может соответствовать нескольким элементам xÎA, где А – носитель множества  , то значение функции принадлежности элемента y нечеткому множеству
, то значение функции принадлежности элемента y нечеткому множеству  определяется как наибольшее из значений, получаемых с помощью выбора минимального между значениями функции принадлежности каждого xÎA нечеткому множеству
определяется как наибольшее из значений, получаемых с помощью выбора минимального между значениями функции принадлежности каждого xÎA нечеткому множеству  и значением функции принадлежности пары <x,y> нечеткому графику
и значением функции принадлежности пары <x,y> нечеткому графику  .
.
Рассмотрим пример нахождения образа множества  .
.
Пусть дано нечеткое соответствие, граф которого приведен на рис. 2.15, нечеткое множество A={<0,6/x1>,<0,7/x2>,<0,9/x4>}. Найти образ  при соответствии
при соответствии  . Для каждого yÎY определим значение mГ(A)(y):
. Для каждого yÎY определим значение mГ(A)(y):
mГ(A)(y1)=(mA(x1)ÙmF<x1,y1>)Ú(mA(x2)ÙmF<x2,y1>)Ú(mA(x4)ÙmF<x4,y1>)=0;
mГ(A)(y2)=(mA(x1)ÙmF<x1,y1>)Ú(mA(x2)ÙmF<x2,y2>)Ú(mA(x4)ÙmF<x4,y2>)=0,2Ú0Ú0,3;
mГ(A)(y3)=(mA(x1)ÙmF<x1,y3>)Ú(mA(x2)ÙmF<x2,y3>)Ú(mA(x4)ÙmF<x4,y3>)=0;
Образом нечеткого множества  при соответствии
при соответствии  является нечеткое множество
является нечеткое множество  ={<0/y1>,<0,3/y2>,<0/y3>}. Справедливы следующие свойства для образов нечетких множеств
={<0/y1>,<0,3/y2>,<0/y3>}. Справедливы следующие свойства для образов нечетких множеств  и
и  множества X при нечетком соответствии
множества X при нечетком соответствии  . Если
. Если  Í
Í  , то
, то 

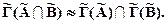
Понятие прообраза нечеткого множества при нечетком соответствии следующее. Пусть  - нечеткое множество, заданное на базовом множестве Y с функцией принадлежности mB, а
- нечеткое множество, заданное на базовом множестве Y с функцией принадлежности mB, а  - нечеткое соответствие.
- нечеткое соответствие.
Прообразом множества  при соответствии
при соответствии  называется нечеткое множество
называется нечеткое множество  , которое задается в X и определяется формулой
, которое задается в X и определяется формулой  где
где
 (2.3)
(2.3)
2.7.2. Основные свойства нечетких соответствий. Рассмотрим такие свойства нечетких соответствий, как нечеткая функциональность, нечеткая инъективность, нечеткая всюду определенность, нечеткая сюръективность, нечеткая биективность.
Свойство функциональности четких соответствий Г=(X,Y,F) предполагает отсутствие в графике F двух пар вида <xi,y1> и <xi,y2>, y1¹y2.
Если использовать понятия прообраза при данном соответствии, то оно будет нефункционально, если для любых двух элементов yi,yjÎY выполняется условие Г-1=(yi)ÇГ-1=(yj)¹Æ. В функциональном соответствии для любых yi,yj справедливо условие Г-1=(yi)ÇГ-1=(yj)=Æ. Аналогичные рассуждения положены в основу определения степеней функциональности и нефункциональности нечеткого соответствия  .
.
Рассматривая каждый элемент yÎY как множество  , у которого mB(y)=1, определим прообраз
, у которого mB(y)=1, определим прообраз  при соответствии
при соответствии  , исходя из формулы (2.3), в следующем виде:
, исходя из формулы (2.3), в следующем виде:  Тогда сможем получить множество нечетких прообразов
Тогда сможем получить множество нечетких прообразов  элементов области прибытия соответствия
элементов области прибытия соответствия  .
.
|
|
|
Степень нефункциональности  соответствия
соответствия  определяется формулой
определяется формулой  т.е. величина
т.е. величина  совпадает с наибольшим значением функции принадлежности тех элементов xÎX, которые являются одновременно нечеткими прообразами любых двух элементов yi, yjÎY.
совпадает с наибольшим значением функции принадлежности тех элементов xÎX, которые являются одновременно нечеткими прообразами любых двух элементов yi, yjÎY.
Соответствие  нечетко функционально, если
нечетко функционально, если  ³0,5.
³0,5.
Степень функциональности  определяется формулой
определяется формулой
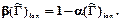
Соответствие  нечетко функционально, если
нечетко функционально, если  ³0,5. Соответствие
³0,5. Соответствие  функционально индифферентно, если
функционально индифферентно, если 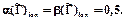
Для четкого соответствия  свойство неинъективности предполагает наличие хотя бы двух элементов x1,x2ÎX, для которых Г(x1)ÇГ(x2)¹0, а свойство инъективности требует - Г(x1)ÇГ(x2)=0. При условии задания произвольного нечеткого соответствия
свойство неинъективности предполагает наличие хотя бы двух элементов x1,x2ÎX, для которых Г(x1)ÇГ(x2)¹0, а свойство инъективности требует - Г(x1)ÇГ(x2)=0. При условии задания произвольного нечеткого соответствия  определим для каждого xÎX нечеткое множество
определим для каждого xÎX нечеткое множество  , используя формулу (2.2), преобразуем к виду:
, используя формулу (2.2), преобразуем к виду:  ={mГ(x)(y)/y>}, yÎY, где mГ(x)(y)=mГ(x)(x,y), т.к. A={x}, mA(x)=1. В результате определим множество
={mГ(x)(y)/y>}, yÎY, где mГ(x)(y)=mГ(x)(x,y), т.к. A={x}, mA(x)=1. В результате определим множество  нечетких образов для всех элементов области отправления соответствия
нечетких образов для всех элементов области отправления соответствия  .
.
Степень неинъективности  соответствия
соответствия  определяется формулой
определяется формулой
 (2.4)
(2.4)
Анализ формулы (2.4) показывает, что величина  совпадает с наибольшим значением функции принадлежности тех элементов yÎY, которые являются одновременно нечеткими образами любых двух элементов.
совпадает с наибольшим значением функции принадлежности тех элементов yÎY, которые являются одновременно нечеткими образами любых двух элементов.
Соответствие  нечетко неинъективно, если величина
нечетко неинъективно, если величина  ³0,5.
³0,5.
Степень инъективности  соответствия
соответствия  определяется формулой
определяется формулой  Соответствие
Соответствие  нечетко инъективно, если величина
нечетко инъективно, если величина  При условии, что величины
При условии, что величины  соответствие
соответствие  инъективно индифферентно.
инъективно индифферентно.
Рассмотрим свойство всюду определенности. Задано произвольное нечеткое соответствие  и для каждого xÎX найден образ
и для каждого xÎX найден образ  . Степень всюду определенности
. Степень всюду определенности  соответствия
соответствия  определяется формулой
определяется формулой  Соответствие
Соответствие  нечетко всюду определено при
нечетко всюду определено при  ³0,5, нечетко не всюду определено при
³0,5, нечетко не всюду определено при  £0,5 и индифферентно относительно всюду определенности при
£0,5 и индифферентно относительно всюду определенности при  =0,5. Если соответствие
=0,5. Если соответствие  нечетко всюду определено, то
нечетко всюду определено, то 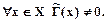
Рассмотрим свойство сюръективности. Для определения свойства сюръективности произвольного нечеткого соответствия  следует определить для каждого yÎY прообраз
следует определить для каждого yÎY прообраз  Степень сюръективности
Степень сюръективности  соответствия
соответствия  определяется по формуле
определяется по формуле
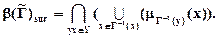
Соответствие  нечетко сюръективно при
нечетко сюръективно при  ³0,5, нечетко несюръективно при
³0,5, нечетко несюръективно при  £0,5, а при
£0,5, а при  =0,5 сюръективно индифферентно. Если соответствие
=0,5 сюръективно индифферентно. Если соответствие  нечетко сюръективно, то
нечетко сюръективно, то
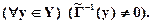
Рассмотрим свойство биективности. Степень нечеткой биективности  произвольного соответствия
произвольного соответствия  определяется формулой
определяется формулой
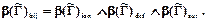
Соответствие  нечетко биективно при
нечетко биективно при  ³0,5, нечетко небиективно при
³0,5, нечетко небиективно при  £0,5 и биективно индифферентно при
£0,5 и биективно индифферентно при  =0.5.
=0.5.
Нечеткие отношения
2.8.1. Задание нечетких отношений. Нечетким отношением на произвольном непустом множестве X называется и через  обозначается пара множеств, в которой
обозначается пара множеств, в которой  является нечетким подмножеством множества X2=X´X. Множество X называется областью задания отношения
является нечетким подмножеством множества X2=X´X. Множество X называется областью задания отношения  , а нечеткое множество
, а нечеткое множество  называется нечетким графиком отношения.
называется нечетким графиком отношения.
Нечеткое отношение  есть нечеткое соответствие
есть нечеткое соответствие  , у которого X=Y. Носителем нечеткого отношения
, у которого X=Y. Носителем нечеткого отношения  называется четкое отношение j=(X,F), у которого график F является носителем графика
называется четкое отношение j=(X,F), у которого график F является носителем графика  . Имеются четыре способа задания нечетких отношений: теоретико-множественный, матричный, графический и с помощью нечетких предикатов (предикатный).
. Имеются четыре способа задания нечетких отношений: теоретико-множественный, матричный, графический и с помощью нечетких предикатов (предикатный).
При теоретико-множественном способе перечисляются последовательно множество X={xi},  и нечеткое множество
и нечеткое множество  ={mF<xi,xj>/<xi,xj>}, xi,xjÎX2.
={mF<xi,xj>/<xi,xj>}, xi,xjÎX2.
Матричный способ требует задания матрицы смежностей Rj, строки и столбцы которой помечены элементами xÎX, а на пересечении i -й строки и j -го столбца указывается элемент rij=mF<xi,xj>, где mF - функция принадлежности элементов xi, xjÎX2 нечеткому графику  .
.
Задание нечеткого отношения  в виде графа предполагает, что граф имеет множество вершин X, а дугам <xi,xj> приписаны соответствующие значения mF<xi,xj>.
в виде графа предполагает, что граф имеет множество вершин X, а дугам <xi,xj> приписаны соответствующие значения mF<xi,xj>.
Нечеткое отношение  , граф которого показан на рис. 2.19, имеет X={x1,x2,...,x5}, F={<0,5/<x1,x5>>, <0,7/<x1,x3>>, <0,4/<x2,x3>>, <0,8/<x3,x3>>, <0,2/<x4,x3>>, <0,1/<x4,x1>>, <0,6/<x5,x4>>, <1/<x5,x3>>, <1/<x5,x5>>}.
, граф которого показан на рис. 2.19, имеет X={x1,x2,...,x5}, F={<0,5/<x1,x5>>, <0,7/<x1,x3>>, <0,4/<x2,x3>>, <0,8/<x3,x3>>, <0,2/<x4,x3>>, <0,1/<x4,x1>>, <0,6/<x5,x4>>, <1/<x5,x3>>, <1/<x5,x5>>}.
Рассмотрим способ задания нечеткого отношения  с помощью нечетких предикатов.
с помощью нечетких предикатов.
Если mF<a,b>/<a,b>Î  , a,bÎX, то выражение
, a,bÎX, то выражение  представляет собой нечеткое логическое высказывание, значение истинности которого равно mF<a,b>. Следовательно, для задания нечеткого отношения
представляет собой нечеткое логическое высказывание, значение истинности которого равно mF<a,b>. Следовательно, для задания нечеткого отношения  на X достаточно задать нечеткую логическую формулу
на X достаточно задать нечеткую логическую формулу  от двух переменных или нечеткий предикат, который определен на множестве X2, а значения принимает из интервала [0,1].
от двух переменных или нечеткий предикат, который определен на множестве X2, а значения принимает из интервала [0,1].

Рис. 2.19
Степень равенства  отношений
отношений  и
и 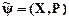 определится выражением
определится выражением
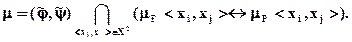
Отношения  и
и  нечетко равны при
нечетко равны при  ³0,5, нечетко не равны при
³0,5, нечетко не равны при  £0,5 и взаимно индифферентны
£0,5 и взаимно индифферентны  при
при  =0,5.
=0,5.
Степенью нечеткости  отношения
отношения  называется величина
называется величина  , где j - носитель нечеткого отношения
, где j - носитель нечеткого отношения  .
.
2.8.2. Операции над нечеткими отношениями. Пусть заданы производные отношения  и
и 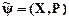 , причем отношение
, причем отношение  нечетко включается в отношение
нечетко включается в отношение  .
.
Объединением отношений  и
и  называется нечеткое отношение
называется нечеткое отношение  , если
, если 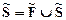 . При этом для любых xi,xjÎX выполняется условие mS<xi,xj>=mF<xi,xj>ÚmP<xi,xj>.
. При этом для любых xi,xjÎX выполняется условие mS<xi,xj>=mF<xi,xj>ÚmP<xi,xj>.
Пересечением отношений  и
и  называется нечеткое отношение
называется нечеткое отношение  , обозначаемое
, обозначаемое  , если
, если  . Для любых xi,xjÎX выполняется условие: mU<xi,xj>=mF<xi,xj>ÙmP<xi,xj>.
. Для любых xi,xjÎX выполняется условие: mU<xi,xj>=mF<xi,xj>ÙmP<xi,xj>.
Дополнением отношения  называется нечеткое отношение
называется нечеткое отношение  , причем для любых xi,xjÎX выполняется условие mF<xi,xj>=1-mF<xi,xj>/
, причем для любых xi,xjÎX выполняется условие mF<xi,xj>=1-mF<xi,xj>/
Инверсией


