Примеры моделей нечетких контроллеров

 

5.2.1. Нечеткое управление подъемно-транспортным механизмом. На рис. 5.4 показана схема разложения на силы при раскачивании груза, который перемешается краном.

 

 

Рис. 5.4. V_T(t) - текущая скорость перемещения крана, a(t) - текущий угол отклонения груза, m - масса груза.

 

Баланс моментов относительно точки О имеет вид М₁+М₂=М₃, где 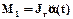- момент инерции груза относительно точки подвеса; - момент, создаваемый составляющей скорости подвеса относительно точки подвеса; M₃=mgl×sina(t) - момент, создаваемый составляющей веса груза относительно точки подвеса. После интегрирования и преобразований получим уравнение:

,

где a(t=0)=a₀, 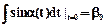- начальные условия нелинейного интерго-дифференциального уравнения.

Сформулируем задачу управления данным нелинейным объектом. На рис. 5.5 показано требуемое изменение текущей скорости V_T(t) перемещения крана.

Необходимо определить скорости V_О(t) в конце торможения по изменениям текущей скорости V_T(t) и угла раскачивания груза a(t).

 

 

Рис. 5.5. О₁ – точка начала разгона, О₂ – точка конца разгона, О₃ – точка начала торможения, О₄ – точка конца торможения.

 

Оператор крана обычно решает данную задачу эвристическим путем, причем, следующее лингвистическое правило может формализовать принятие решения оператором о выборе скорости V_О(t) в конце торможения:

R_i: если угол da=a_з-a, где a_з - заданное значение, a - измеренное значение a; немного увеличивается по часовой стрелке и производная угла колебания груза немного увеличивается против часовой стрелки и скорость dV_T=V_TЗ-V_T, где V_TЗ – заданное значение скорости, V_T - измеренное значение скорости; равна нулю, тогда скорость V_О должна быть небольшой в отрицательном направлении относительно нуля.

Введем лингвистические переменные (ЛП): da - «угол раскачивания», - «производная угла раскачивания»; dV_T – «разность заданной и измеренной скоростей»; V_О – «определяемая скорость». Согласно работе [13], для ЛП введем нечеткие переменные (НП).

Определим терм-множество ЛП da: Т(da)={PM _da - угол раскачивания da положительный (против часовой стрелки) средний; PS _da - угол раскачивания da положительный небольшой; ZR _da - угол раскачивания da нулевой; NS _da - угол раскачивания da отрицательный (против часовой стрелки) небольшой; NM _da – угол раскачивания da отрицательный средний}. На рис. 5.6 приведены функции принадлежности m_da для нечетких переменных терм-множества Т(da).

Определим терм-множество ЛП : Т()={PS - производная угла раскачивания положительная небольшая; ZR - производная угла раскачивания нулевая; NS - производная угла раскачивания отрицательная}. На рис. 5.7 приведены функции принадлежности 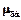для нечетких переменных терм-множества Т().

Определим терм-множество ЛП dV_T: Т(dV_T)={PM - разность скоростей dV_T положительная (против часовой стрелки) средняя; PS - разность скоростей dV_T положительная небольшая; ZR - разность скоростей dV_T нулевая; NS - разность скоростей dV_T отрицательная (против часовой стрелки) небольшая; NM – разность скоростей dV_T отрицательная средняя}. На рис. 5.8 приведены функции принадлежности m(dV_T) для нечетких переменных терм-множества Т(dV_T).

 

Рис. 5.6

 

Рис. 5.7

 

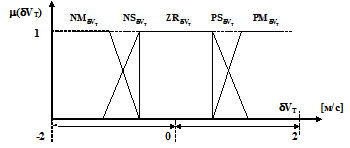
Рис. 5.8

Определим терм-множество ЛП dV_О: Т(V_О)={PM _VО - скорость V_О положительная (против часовой стрелки) средняя; PS _VО - скорость V_О положительная небольшая; ZR _VО - скорость V_О нулевая; NS _VО - скорость V_О отрицательная (против часовой стрелки) небольшая; NM _VО – скорость V_О отрицательная средняя}. На рис. 5.9 приведены функции принадлежности m(V_О) для нечетких переменных терм-множества Т(V_О).

Рис. 5.9

Для точки O₄ определим следующую базу правил эвристического алгоритма управления оператором скоростью V_O(t) крана при V_T(t)=0:

R₁: если da=NS_da и =NS и dV_T=ZR , тогда V_О=ZR_VО;

R₂: если da=NS_da и =ZR и dV_T=ZR , тогда V_О=NS_VО;

R₃: если da=NS_da и =PS и dV_T=ZR , тогда V_О=NS_VО;

R₄: если da=ZR_da и =NS и dV_T=ZR , тогда V_О=PS_VО;

R₅: если da=ZR_da и =ZR и dV_T=ZR , тогда V_О=ZR_VО;

R₆: если da=ZR_da и =PS и dV_T=ZR , тогда V_О=NS_VО;

R₇: если da=PS_da и =NS и dV_T=ZR , тогда V_О=PS_VО;

На рис 5.10 показано решение об изменении скорости крана для предотвращения раскачивания груза в точке O₄.

 

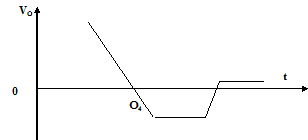
Рис. 5.10

Аналогичные базы правил изменения скоростных режимов можно составить для точек O₁ - O₃.

Объединение правил для всех точек O₁ - O₄ позволит получить формализованное представление эвристического алгоритма управления скоростью перемещения крана. Если затем разработать нечеткий контроллер, то можно построить систему управления, которая без оператора будет решать задачу управления скоростью перемещения крана для предотвращения опасного раскачивания груза.

Блок-схема нечеткой системы управления приведена на рис. 5.11.

 

Рис. 5.11

 

Очевидно преимущество за счет простоты реализации нечеткой системы управления (регулирования) нелинейным объектом (краном) по сравнению с традиционной системой регулирования.

В практике разработки технических систем подобные задачи встречаются очень часто. Это системы регулирования для всевозможных подъемно-транспортных механизмов.

5.2.2. Гибридная система регулирования. Объектом для регулирования принят асинхронный электропривод с частотным преобразователем. На рис. 5.12 приведена структурная схема системы регулирования асинхронного электропривода с ПД-регулятором в цепи обратной связи.

 

Рис. 5.12

 

Передаточная функция электропривода определена формулой:

,

где Q(s) – угол поворота вала двигателя; U(s) – управляющий сигнал; p – динамический параметр объекта; s – переменная преобразования Лапласа; k – коэффициент усиления двигателя; W₁(s)=k_p – передаточная функция П-регулятора в прямой цепи регулирования; W₂(s) – передаточная функция измерительного устройства; W₃(s)=k_vs – передаточная функция ПД-регулятора в цепи обратной связи; R(s) – задание; E(s) – ошибка в отработке задания.

Передаточная функция замкнутой системы управления определится формулой:

,

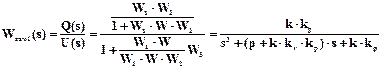из которой получим:

,

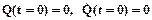. (5.1)

Переходная характеристика системы имеет вид, показанный на рис. 5.13.

 

Рис. 5.13

 

Уравнение (5.1) позволяет определить коэффициент затухания колебаний

,

где l - частота затухающих колебаний, причем g=g(k_p,k_v).

Очевидно, что при росте коэффициентов усиления k_p,k_v увеличивается коэффициент g, что приводит к появлению нежелательных скачков углов поворота вала двигателя, а установившаяся ошибка в отработке задания не зависит от коэффициентов усиления k_p,k_v, т.к. E(t=¥)=R(t=¥)-h(t=¥)=0.

Применение обратного преобразования Лапласа к передаточной функции замкнутой системы позволяет получить уравнение для управления:

U(t)=k_pE(t)-k_pk_v .

Если , где t - шаг дискретизации, то получим уравнение U=k_pE-k_pk_v , которое применяют для реализации ПД-регулятора в виде программы контроллера.

ПД-регулятор может быть применен также и ввиде последовательного корректирующего звена, как это показано на риc. 5.14.

 

Рис. 5.14

 

Передаточная функция замкнутой системы управления определится формулой

,

из которой получим:

,

. (5.2)

Из уравнений (5.1) и (5.2) следует, что при реализации первой (см. рис. 5.12) и второй (см. рис. 5.14) систем управления учитываются разные виды дифференциальных уравнений, которые описывают замкнутую систему управления. Первой и второй структурам систем управления присущ общий недостаток, состоящий в том, что из-за отсутствия знаменателей в передаточных функциях регуляторов происходит усиление высокочастотных колебаний, которые подаются на вход объекта управления, что приводит к нежелательным последствиям (перегрев, пробой изоляции и т.д.).

Осуществим решение задачи подавления высокочастотных колебаний путем проектирования замкнутой системы управления, структура которой представлена на риc. 5.15.

 

Рис. 5.15

 

Передаточная функция регулятора может быть выбрана из условия

W_зам3(s)=W_зам1(s), (5.3)

где W_зам3(s) - передаточная функция замкнутой системы, приведенной на рис. 5.15, либо из условия W_зам3(s)=W_зам2(s).

Из условия (5.3) определим W_x(s):

.

Это позволяет определить, что

.

Из вида W_x(s) следует, что W_x(s) представляет собой ПИД-регулятор, который фильтрует высокочастотные колебания, причем

,

откуда

k_p(s+p)E(s)=[s+(p+kk_vk_p)]U(s).

Обратное преобразование Лапласа позволяет перейти в пространство оригиналов и получить дифференциальное уравнение:

.

При , DE=E(t)-E(t-t), Du=u(t)-u(t-t) получим

.

Данное уравнение является моделью ПИД-регулятора в цифровой форме.

Структура замкнутой системы управления асинхронным двигателем, приведенная на рис. 5.15, позволяет решить задачу фильтрации высокочастотных колебаний при задании R(t)¹1(t). При любом другом виде задания R(t) эта структура не обеспечивает должной по скорости обработки этого сигнала. Поэтому предлагается в структуру замкнутой системы управления ввести нечеткий регулятор, в котором существует алгоритм обработки нечетких высказываний относительно зависимости коэффициента усиления от ошибки G(E). Структура замкнутой системы управления асинхронным двигателем примет вид, приведенный на рис. 5.16.

В данной системе обычный ПИД-регулятор настраивает коэффициент усиления G в зависимости от величины ошибки E(t). Если величина ошибки E(t) невелика, то в гибридном регуляторе используется величина коэффициента усиления G, принятая для обычного ПИД-регулятора. При больших значениях величины ошибки E(t) скорость изменения коэффициента усиления G уменьшается.

 

 

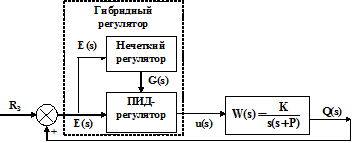
Рис. 5.16

 

Зависимость коэффициента усиления от ошибки G(E) представлена на рис. 5.17.

 

Рис. 5.17

 

Введем лингвистические переменные (ЛП): e - «величина ошибки E», d – «величина коэффициента усиления G».

Определим терм-множество ЛП e: Т(e)={PB _e - величина ошибки E положительная и большая; PM _e - величина ошибки E положительная и средняя; PS _e - величина ошибки E положительная и небольшая; ZR _e - величина ошибки E нулевая; NS _e - величина ошибки E отрицательная и небольшая; NM _e – величина ошибки E отрицательная и средняя; NB _e – величина ошибки E отрицательная и большая}. На рис. 5.18 приведены функции принадлежности m_e для нечетких переменных терм-множества Т(e).

Определим терм-множество ЛП g: Т(g)={PB _g - величина коэффициента усиления G положительная и большая; PM _g - величина коэффициента усиления G положительная и средняя; PS _g - величина коэффициента усиления G положительная и небольшая; ZR _g - величина коэффициента усиления G нулевая; NS _g - величина коэффициента усиления G отрицательная и небольшая; NM _g – величина коэффициента усиления G отрицательная и средняя; NB _g – величина коэффициента усиления G отрицательная и большая}. На рис. 5.19 приведены функции принадлежности m_g для нечетких переменных терм-множества Т(g).

 

Рис. 5.18

 

Рис. 5.19

 

На рис. 5.20 приведена зависимость изменения сигнала управления u(t) для ПИД- и гибридного регулятора [11]. При управлении частотным преобразователем гибридный регулятор обладает преимуществами перед ПИД- регулятором.

 

Рис. 5.20

 

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Бурбаки Н. Теория множеств. – М.: Мир, 1965. – 455с.

2. Мелихов А.Н., Берштейн Л.С. Конечные четкие и расплывчатые множества. Часть I. Четкие множества. – Таганрог: ТРТИ, 1980. – 101с.

3. Аверкин А.Н., Батыршин И.З., Блишун А.Ф., Силов В.Б., Тарасов В.Б. Нечеткие множества в моделях управления и искусственного интеллекта / Под ред. Поспелова Д.А. - М.: Наука, 1986.

4. Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. - М.: Наука, 1990.

5. Борисов А.Н., Алексеев А.В., Крумберг О.А. и др. Модели принятия решений на основе лингвистической переменной. - Рига: Зинатне, 1982.

6. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.: Мир, 1976. – 165 с.

7. Мелихов А.Н., Баронец В.Д. Проектирование микропроцессорных устройств обработки нечеткой информации. - Ростов-на-Дону.: Изд-во Ростовского университета, 1990. 128 с.

8. Берштейн Л.С., Финаев В.И. Адаптивное управление с нечеткими стратегиями. - Ростов н/Д.: Изд-во Рост. ун-та, 1993. 134 с.

9. Берштейн Л.С., Боженюк А.В. Нечеткий логический вывод на основе определения истинности нечеткого правила modus ponens // Методы и системы принятия решений. Системы, основанные на знаниях. Рига: РПИ, 1989. С. 74-80.

10. Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике: Пер. с фр. М.: Радио и связь. 1990. 288 с.

11. Методы робастного, нейро-нечеткого и адаптивного управления: Учебник/Под ред. Н.Д.Егупова; издание 2-ое, стереотипное. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 744 с.

12. Берштейн Л.С., Боженюк А.В. Нечеткие модели принятия решений: дедукция, индукция, аналогия. Монография. – Таганрог: Изд-во ТРТУ, 2001. – 110 с.

13. Ли Р. Оптимальные оценки, определение характеристик и управление. М.: Наука, 1966.

 

 

 

Финаев Валерий Иванович

 

 

МОДЕЛИ CИCТЕМ ПРИНЯТИЯ РЕШЕНИЙ

 

Ответственный за выпуск Финаев В.И.

Редактор Белова Л.Ф.

Корректор Селезнева Н.И.

 

ЛП №020565 Подписано к печати 23.11.05

Офсетная печать Усл. п.л. – 8,1 Уч.-изд.л. – 7,9

Заказ №_______ Тирах 350 “С”

 

_____________________________________________________

Издательство Таганрогского государственного

радиотехнического университета

ГСП 17А, Таганрог, 28, Некрасовский, 44

Типография Таганрогского государственного

радиотехнического университета

ГСП 17А, Таганрог, 28, Энгельса, 4

 

⇐ Предыдущая3456789101112

Поделиться:

Воспользуйтесь поиском по сайту: