 |
Классификация связей, число степеней свободы, независимые обобщенные координаты
|
|
|
|
ОСНОВЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ. КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ
Утверждено советом университета
В качестве учебного пособия
Санкт-Петербург
Оглавление
Введение.
1.Возможные перемещения. Обобщенные силы
1.1. Элементарные и возможные перемещения
1.2. Работа силы на элементарном и возможном перемещении
1.3. Обобщенные силы
1.4. Силовое поле. Потенциальная энергия. Обобщенные силы для консервативных систем
1.5. Вопросы и задачи для самоконтроля
2. Принцип возможных перемещений
2.1. Условия равновесия и покоя механической системы
2.2. Условия равновесия в обобщенных координатах и силах
2.3. Вопросы и задачи для самоконтроля
3. Общее уравнение динамики механической системы
3.1. Общее уравнение динамики (принцип Даламбера – Лагранжа)
3.2. Уравнения Лагранжа первого рода
3.3. Вопросы и задачи для самоконтроля
4. Уравнение Лагранжа второго рода
4.1. Вывод уравнений
4.2. Уравнения Лагранжа второго рода для консервативных систем
4.3. Циклические координаты. Циклические интегралы
4.4. Особенности применения уравнений Лагранжа второго рода для систем с неидеальными связями
4.5. Особенности применения уравнений Лагранжа второго рода для систем с неудерживающими связями
4.6. Уравнения движения для неголономных систем с множителями Лагранжа *
4.7. Вопросы и задачи для самоконтроля
5. Колебания линейных механических систем около положения устойчивого равновесия
5.1. Общие замечания
5.2. Определение положения равновесия
5.3. Устойчивость положения равновесия
5.4. Колебания линейной механической системы с одной степенью свободы около положения устойчивого равновесия
5.5. Колебания линейной механической системы с двумя степенями свободы около положения устойчивого равновесия
|
|
|
5.6. Вопросы и задачи для самоконтроля
6. Литература
Введение
Аналитическая механика является логическим развитием материала, знакомого читателю по курсу теоретической механики: здесь используются те же модели пространства, времени, тел и их взаимодействий (конечно, с некоторым развитием и добавлением новых понятий). Опираясь на энергетические подходы, аналитическая механика позволяет единообразно составлять уравнения покоя и движения свободных и несвободных механических систем с любым числом степеней свободы, а так же приводить эти уравнения к виду, удобному для интегрирования. На протяжении длительного существования аналитической механики в ней разработаны эффективные общие методы исследований, которые проникли в прикладную математику, теорию оптимального управления, термо- и электродинамику, статистическую физику и квантовую механику.
Среди процессов как свободно протекающих в природе, так и используемых в технике видное место занимают колебания. Научной основой решения самых разнообразных технических задач служит теория колебаний. В настоящем пособии рассмотрены простейшие вопросы колебаний механических систем, а именно колебания линейных систем с одной и двумя степенями свободы.
Классификация связей, число степеней свободы, независимые обобщенные координаты
Кратко напомним понятия, обсуждавшиеся ранее в [6,7,8].
Тела и материальные точки, положение и скорость движения которых не ограничены другими телами, называются свободными; в противном случае они несвободные, а тела, ограничивающие их движение, называются связями.
Любую выделенную для анализа совокупность взаимодействующих тел и материальных точек называют механической (реже - материальной) системой.
Положения всех точек механической системы в выбранной системе отсчета могут быть определены некоторым набором скалярных величин. В случае покоя эти скалярные величины постоянны, а при движении они являются функциями времени. Такие величины называются обобщенными координатами. Поясним это понятие на системах, точки которых расположены в трехмерном пространстве.
|
|
|
За обобщенные координаты свободной точки могут быть приняты декартовы координаты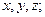 
за обобщенные координаты системы из двух свободных точек - 
и т.д.
Для абсолютно твердого тела в форме жесткого прямого стержня длины 
(рис.В.1.а) достаточно задаться координатами двух его точек (например, концевых) и учесть, что расстояние между ними неизменно, т.е. шесть декартовых координат этих точек (рис.В.1.а) связаны соотношением
(В.1)
Равенства типа (В.1) характеризуют наложенные на систему связи и называются уравнениями связей. Связи, уравнения которых содержат только координаты и время, называются геометрическими, так как обычно им соответствуют простые геометрические образы (линия, плоскость и т.д.).
Рассмотрим механическую систему из двух шарнирно соединенных стержней с длинам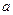и 
и 
. Принимая за обобщенные координаты декартовы координаты концевых точек стержней (рис.В.1.б), следует иметь в виду, что эти координаты связаны двумя уравнениями связей:
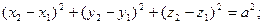
(В.2)
Если рассмотренная механическая система движется в плоскости, например Oxy, то уравнения связей (В.2) следует дополнить уравнениями 
. Однако если оговорено, что решается плоская задача, в литературе по механике обычно ограничиваются записью
Все перечисленные примеры обладают стационарными или склерономными геометрическими связями. В уравнениях таких связей время 
не содержится в явном виде (хотя неявная зависимость от времени через координаты, конечно, имеется).
Пример системы с нестационарной или реономной связью показан на рис.В.1.в., где материальная точка 
связана с началом координат нитью переменной длины; закон изменения во времени этой длины 
задан. Если нить натянута, уравнение связи имеет вид
(В.3)
Кроме того, все оговоренные типы связей аналитически описываются равенствами. Такие связи в механике принято называть двусторонними или удерживающими. Односторонние или н еудерживающие связи описываются неравенствами. Например, для случая ненатянутой нити будет справедлива запись
|
|
|
(В.4)
В приведенных выше уравнениях связей нет производных от координат. Такие связи называются голономными или интегрируемыми (выше мы их назвали геометрическими). Например, при изучении плоского движения для катящегося без скольжения колеса радиуса R было получено кинематическое соотношение 
, где 
- скорость центра О колеса, а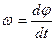 
- угловая скорость его вращения. Уравнения такого типа ранее назывались уравнениями кинематических связей. Не трудно заметить, что хотя в уравнении кинематической связи содержатся производные от координат 
и 
, интегрированием их можно исключить. В частности, при нулевых начальных условиях, получится новое уравнение связи 
, не содержащее производных.
Если в уравнениях связей присутствуют производные координат, от которых невозможно избавиться интегрированием, такие связи называются неголономными или неинтегрируемыми.
Наличие уравнений связей означает, что выбранные координаты зависимы. Однако в большинстве случаев (если механическая система голономна) можно, изменив выбор, указать независимые обобщенные координаты, т.е. такие, между которыми не существует уравнений связей.
Так, для системы, изображенной на рис.В.1.а, за одну из
возможных совокупностей обобщенных координат можно принять декартовы координаты первой точки 
и углы 
между направлением стержня и осями абсцисс и ординат, соответственно (см. рис.В.2.а), а для системы, изображенной на
рис.В.1.б, - координаты первой точки и углы 
и 
между направлениями стержней и осью абсцисс, и углы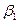 
и 
между направлениями стержней и осью ординат (см. рис.В.2.б).
Ясно, что при таком выборе обобщенных координат однозначно определены положения всех точек каждой из рассматриваемых механических систем.
Важной количественной характеристикой общих структурных свойств механической системы служит число степеней свободы. Если за обобщенные координаты выбраны такие, что между ними существуют уравнения связей, то число степеней свободы можно найти как разность числа этих координат и числа уравнений связей.
|
|
|
Например, если на механическую систему из 
точек в трехмерном пространстве наложено голономных связей, то число независимых обобщенных координат совпадает с числом степеней свободы 
, которое может быть рассчитано, в этом случае, как 
.
Если на механическую систему из точек в трехмерном пространстве наложено голономных связей и 
неголономных связей, то число степеней свободы 
для такой системы должно быть рассчитано, как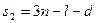 
; при этом число независимых обобщенных координат останется прежним.
Разумеется, на число степеней свободы влияют не только внутренние, но и внешние связи.
Все последующие рассуждения и выводы будут относиться только к голономным, стационарным и удерживающим связям (если связи неголономные, нестационарные либо неудерживающие, то это будет оговариваться особо).
При анализе движения несвободных систем действующие силы удобно разделять на активные (задаваемые) и реакции связей. Ранее, при изучении теоремы об изменении кинетической энергии механической системы, было введено понятие идеальной связи (реакции такой связи не совершает работу в процессе движения механической системы. Примеры – скольжение по гладкой поверхности, качение без проскальзывания и т.д.). Заметим, что в литературе по аналитической механике (и ниже в настоящем пособии) используется несколько иное определение этого понятия.
|
|
|
