 |
Наиболее ранний срок наступления события
|
|
|
|
Напомним, что событие соответствует некоторому узлу, представляет собой момент завершения одной или большего числа работ и может быть отправным моментом для начала последующих работ.
Наиболее ранним возможным сроком наступления j-го события является наиболее ранний возможный срок завершения всех работ, подходящих к j-му узлу.
Пусть ljр — наиболее ранний возможный срок наступления j-го события, j=0,1, 2,..., n, где n+1 — число событий (узлов) в сети. Величина tij — продолжительность работы, соединяющей два события (узлы) — i-е и j-е.
Поскольку j-е событие не может произойти, пока не будут завершены все работы, ведущие к j-му узлу, и поскольку работа не может начаться, пока не произойдет предшествующееейсобытие, наиболее ранний возможный срок наступления каждого события вычисляется как продолжительность самого длинного пути от начального события до данного. Так как в сети установлена правильная нумерация, то ljр можно вычислять последовательно, начиная с l0р =0, по формуле
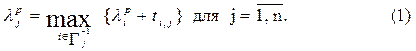 |
Применяя формулу (1), предлагается запоминать для каждого j значение ljри номер i(j), на котором достигается максимальное значение. Это позволит по окончании вычислений найти не только величину наиболее длинного пути, но и сам этот путь.
Наиболее длинный путь из начального события в конечное называется критическим путем.
Длину критического пути обозначим Ткр. Тогда Ткр=lnр. Узлы, через которые проходит критический путь можно легко получить, исходя из следующего алгоритма:
Конечный узел критического пути всегда имеет номер n,
Если узел с номером j принадлежит критическому пути, то номер предшествующего ему узла равен i(j) (см.формулу (1)),
|
|
|
Начальный узел всегда имеет номер 0.
Длина критического пути определяет минимальное время, необходимое для завершения проекта.
Пример 2.
Для всех узлов (событий) сети из примера 1 определить наиболее ранний возможный срок наступления события и критический путь.
Последовательно применяя формулу (1) для j=0,1,2,3,…,8, получаем
l0р=0, предшествующего события здесь нет.
l1р=max{l0р+t0,1}=max{0+4}=4, i(1)=0.
l2р=max{l0р+t0,2}=max{0+6}=6, i(2)=0.
l3р=max{l2р+t2,3}=max{6+7}=13, i(3)=2.
l4р=max{l0р+t0,4, l3р+t3,4}=max{0+9,13+0}=13, i(4)=3.
l5р=max{l1р+t1,5, l3р+t3,5}=max{4+8,13+0}=13, i(5)=3.
l6р=max{l4р+t4,6, l5р+t5,6}=max{13+10,13+6}=23, i(6)=4.
l7р=max{l6р+t6,7}=max{23+4}=27, i(7)=6.
l8р=max{l7р+t7,8}=max{27+9}=36, i(8)=7.
Итак, для каждого события найден наиболее ранний возможный срок его наступления, определяющий момент времени, начиная с которого это событие становится возможным. Длина критического пути равна Ткр= l8р=36. Критический путь проходит через следующие узлы сети:
8, i(8)=7, i(7)=6, i(6)=4, i(4)=3, i(3)=2, i(2)=0.
Следовательно, в данном примере критический путь имеет вид
(0,2)-(2,3)-(3,4)-(4,6)-(6,7)-(7,8).
Наиболее поздний срок наступления события
Наиболее поздним допустимым сроком наступления i-го события является наиболее поздний срок завершения всех работ, идущих к i-му узлу, не влияющий на время завершения всего проекта за Ткр.
Пусть liп ¾ наиболее поздний допустимый срок наступления i-го события. Чтобы гарантировать, что продолжительность критического пути не будет превышена, необходимо положить lnп =Ткр.
Начиная с n-го события, двигаемся в обратном направлении к событию 0, вычисляя очередное liп при i<n по формуле
и номер j*(i), при котором достигается минимум.
 |
Вычисления ведутся до тех пор, пока не будет определен наиболее поздний срок наступления начального события (событие 0).
Пример 3.
Для всех узлов (событий) сети из примера 1 определить наиболее поздний допустимый срок наступления события.
Полагаем l8п =Ткр=36. Затем последовательно применяя формулу (2) для j=8,…,1, получаем
|
|
|
l7п=min{l8п- t7,8}=min{36-9}=27, j*(i)=8,
l6п=min{l7п-t6,7}=min{27-4}=23, j*(i)=7,
l5п=min{l6п-t5,6}=min{23-6}=17, j*(i)=6,
l4п=min{l6п-t4,6}=min{23-10}=13, j*(i)=6,
l3п=min{l4п-t3,4, l5п-t3,5}=min{13-0,17-0}=13, j*(i)=4,
l2п=min{l3п-t2,3}=min{13-7}=6, j*(i)=3,
l1п=min{l5п-t1,5}=min{17-8}=9, j*(i)=5,
l0п=min{l1п-t0,1,l4п-t0,4, l2п-t0,2}=min{9-4,13-9,6-6}=0, j*(i)=2.
Отметим, что при правильно проведенных вычислениях всегда должно получиться l0п =0.
|
|
|


