 |
Примеры решения задач к теме 6, 7.
|
|
|
|
Задача 1
Предположим, что обратная функция спроса для олигополии Курно задается выражением
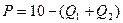
и что стоимостные функции равняются нулю.
1) Каковы будут в этом случае предельные поступления каждой компании?
2) Каковы функции реагирования для каждой компании?
3) Каковы значения объемов выпускаемой продукции для равновесия Курно?
4) Какова равновесная цена?
Ответ
1)Использовав формулы для предельных поступлений для олигополии Курно, получим
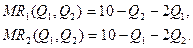
2) Аналогично, воспользовавшись соответствующими формулами, получим
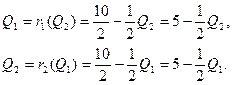
3) Чтобы определить значения объемов выпускаемой продукции при равновесии Курно, необходимо решить систему из двух уравнений (функций реагирования) с двумя неизвестными:
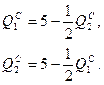
Подставив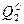 
в первую функцию реагирования, получим
Решая это выражение относительно 
, получим
Чтобы определить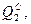 
подставим 
в функцию реагирования для компании 2 и получим
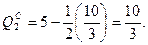
4) Общий объем выпускаемой продукции в отрасли равен
Рыночная цена определяется (обратным) спросом при вычисленном значении общего количества продукции:
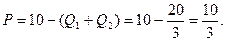
Задача 2
Предположим, что обратная функция спроса для двух компаний, выпускающих одну и ту же продукцию, на рынке с олигополией Штакелберга задается выражением
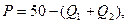
а стоимостные функции –
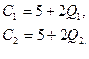
Компания 1 является «зачинщиком», а компания 2 – «преследователем».
1) Какова функция реагирования для компании 2?
2) Какова функция прибыли для компании 1?
3) Каков объём выпускаемой продукции компании 1?
4) Каков объём выпускаемой продукции компании 2?
5) Какова рыночная цена?
Ответ
1) Используя формулу для функции реагирования для «преследователя», получим, что
.
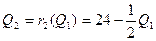2) Подставив из п.1) в функцию прибыли для «зачинщика» в олигополии Штакелберга, получим, что
|
|
|
.
3) Используя формулу для «зачинщика» в олигополии Штакелберга, получим, что
.
4) Подставив ответ из п.3) в функцию реагирования из п. 1), получим, что объём выпускаемой продукции «преследователя» равен
.
6) Рыночную цену можно определить, если сложить объёмы выпускаемой продукции обеих компаний и подставить полученное значение в обратную функцию спроса, т.е.
.
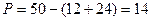Задача 3.
В одном городе два инвестора собираются построить по одному кирпичному заводу. Предполагается, что функции затрат после введения их в эксплуатацию идентичны и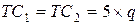 
. Ожидаемый спрос описывается формулой 
, где q1 и q2 – предложение первого и второго производителя соответственно. Каждый завод должен определить оптимальный размер производства с точки зрения получения максимальной прибыли.
Задание: определить производственные мощности заводов, цены, концентрацию на рынке и прибыли производителей при:
1. сговоре между предприятиями (модель картеля);
2. при независимом поведении производителей (модель Курно);
3. в случае, когда один из производителей является лидером и первым определяет размер собственного производства (модель Штакельберга).
4. рассчитать уровень концентрации производства.
Ответ
Е) Картель.
При сговоре предполагается, что предприятия, максимизируют свою общую прибыль, ограничивая общее предложение.
Пусть 
. Равновесие достигается в случае максимизации общей прибыли. Это соответствует решению следующей задаче:
.
Дифференциальная характеристика равновесия может быть записана в такой форме:
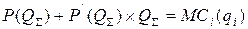, где МС – предельные затраты производителей и равны производной функции затрат по q.
В данной задаче предельные затраты производителей равны. Получаем цену и суммарную мощность заводов:
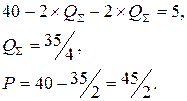
Однозначное распределение прибыли (и долей рынка) отсутствует, однако исходя из равенства функций затрат можно предположить, что размер производства одинаковый: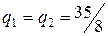 
.
|
|
|
Тогда значение индекса концентрации равно квадрату долей рынка:
HHI = (½)2 + (½)2 = 0,5.
Суммарная прибыль pS = (q1 +q2)(P – AC) = (35/4)(45/2 – 5) = (35)2/8.
Прибыль каждого завода равна: p1 = p2 = q1 (P – AC) = (35/4)(45/2 – 5) = (35)2/16.
F) Модель Курно.
При независимом поведении предполагается, что каждый производитель максимизирует собственную прибыль при каждом заданном объеме производства конкурента.
Задача каждого предприятия может быть представлена следующим образом:
,
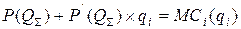где P’(QS) – производная функции спроса.
В данной задаче это соответствует системе уравнений:
,
,
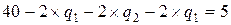выразим из первого уравнения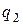 
:
.
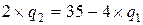Теперь подставим данное выражение во второе уравнение:
.
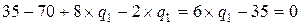Отсюда получаем для каждого производителя объем производства, суммарное предложение кирпича и цену:
, 
, 
, 
.
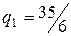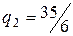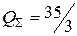Тогда значение индекса концентрации равно квадрату долей рынка:
HHI = (½)2 + (½)2 = 0,5.
Прибыль каждого предприятия равна: p 1 = p2 = q1 (P – AC) = (35/6)(50/3 – 5) = 352/18.
Суммарная прибыль pS = p1 + p2 = 352/9.
G) Модель Штакельберга.
Пусть фирма 1 является лидером, то есть определяет размер собственного производства кирпича, прогнозируя отклик конкурентов. Отклик второй фирмы определяется как объем производства, позволяющий при данном производстве первой фирмы максимизировать прибыль:
.
В данной задаче отклик фирмы может быть определен из второй формулы модели Курно следующим образом:
.
Задача фирмы-лидера может быть сформулирована следующим образом:
В данной задаче это соответствует следующей записи:
.
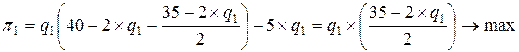Таким образом, получаем:
.
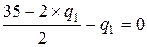В итоге решением данной задачи являются следующие размеры производства кирпича и цены:
, 
, 
, 
.
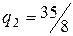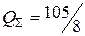h) Значение индекса концентрации равно квадрату долей рынка:
HHI=(2/3)2 + (1/3)2 = 5/9.
Прибыль первой фирмы равна: p1 = q1 (P – AC) = (35/4)(55/4 – 5) = 352/16.
Прибыль второй фирмы равна: p2 = q2 (P – AC) = (35/8)(55/4 – 5) = 352/32.
Суммарная прибыль pS = p1 + p2 = 352(3/32).
Задача 4
В городе работает две гостиницы с идентичными функциями затрат 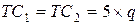, где q – число предлагаемых номеров.
Спрос на рынке описывается формулой . Определить:
38. размер предоставляемых услуг, цены и концентрацию на рынке при ценовой конкуренции между гостиницами (модель ценовых войн Бертрана);
|
|
|
39. диапазон колебания цен при ограничении числа номеров каждой из гостиниц половиной максимальной емкости рынка (модель Эджворта);
40. уровень цен, объем оказанных услуг и уровень концентрации при неполной заменяемости услуг каждой гостиницы (наличии дополнительных услуг, позволяющих говорить о дифференциации услуг); при этом спрос на услуги каждой гостиницы задается формулами:
q1 = 10 -P1 / 2 + P2 / 4;
q2 = 10 -P2 / 2 + P1 / 4;
41. проанализировать полученные результаты.
Ответ
Е) Модель Бертрана.
Парадокс Бертрана заключается в том, что при установлении цены выше, чем у конкурирующих фирм приводит к отсутствию продаж. При этом фирма, «подрезая» цену конкурента, получает весь рынок. Долгосрочное равновесие на такого рода рынке устанавливается только в ситуации, когда:
.
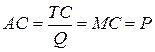В модели Бертрана нет однозначного решения в краткосрочном периоде, однако в долгосрочном периоде все фирмы устанавливают минимальную цену в размере средних затрат (в данном случае средние затраты равны предельным). В противном случае фирма-конкурент может назначить более низкую цену.
Таким образом, равновесное состояние достигается при цене:
P = MC = AC = 5.
|
|
|
