 |
При этом емкость рынка будет максимальной и составит
|
|
|
|
QS = (40 - 5) / 2 = 35 / 2
Соответственно, спрос на номера каждой из гостиниц составит q1=q2=35/4.
Тогда значение индекса концентрации равно квадрату долей рынка:
HHI = (½)2 + (½)2 = 0,5.
Прибыли каждой из фирм равны 0.
F) Модель Эджворта.
В рамках модели Эджворта предположим, что размер каждой гостиницы ограничен и равен половине максимально возможного выпуска (что означает, что у гостиниц нет дополнительных номеров). Максимально возможный выпуск достигается при минимальной цене, равной средним затратам: 35/2. Тогда ограничения мощности каждой фирмы равны соответственно
K1 = K2 = 35 / 4.
В этих условиях существует две оптимальные стратегии поведения каждой фирмы в зависимости от поведения конкурента.
Пусть фирма 1 устанавливает минимальную цену и максимальный объем производства: P1=5, q1 = K1 = 35/4. Данный объем предложения не может удовлетворить весь спрос на рынке. Тогда оптимальной стратегией фирмы 2 является стратегия максимизации прибыли на остаточном спросе. Остаточный спрос на продукцию фирмы 2 равен:
RD = (40 - P2) / 2 - 35 / 4 = 45 / 4 - P2 / 2.
Отсюда цена спроса на номера во второй гостинице определяется формулой:
P2 = 45/2 - 2q2.
Тогда условие максимизации прибыли выглядит следующим образом:
MR = 45/2 - 4q2 = 5.
Предложение номеров, цена номера и прибыль фирмы следующие:
q2 = 35/8; P2 = 55/4; p2 = (35/8)(55/4 - 5) = 35/8 *35/4.
Теперь предположим, что фирма 1 устанавливает высокую цену. Тогда оптимальной стратегией фирмы 2 является «подрезание цены» первой фирмы.
Если P1 = 45/2, тогда при цене P2 = 44/2 = 22 спрос на продукцию фирмы 2 равен q2 = (40 - 22) / 2 = 9, что больше производственных мощностей фирмы 2. То есть объем производства равен производственным мощностям K2.
Найдем минимальную цену, при которой эффективна стратегия «подрезания цены».
|
|
|
Прибыль фирмы 2 при подрезании цены равна:
p2 = (P1 - 5 - e)K2» (P1 - 5)K2, где e - бесконечно малая величина.
Применение стратегии имеет смысл только в случае, когда прибыль от подрезания цены выше прибыли, полученной при максимизации прибыли на остаточном спросе. Минимальная прибыль при максимизации прибыли на остаточном спросе равна 35/8 *35/4.
Тогда минимальная цена, начиная с которой выгодно устанавливать цену ниже, чем у конкурента, определяется из решения неравенства:
(P1 - 5)K2 = (P1 - 5)35/4 > 35/4 * 35/8, откуда
P1 = 75/8, P2 = P1 -e» 75/8.
Диапазон колебания цен [75/8; 110/8].
G) Модель дифференциации продукта.
Предположим, что каждая из гостиниц не является идеальным заменителем другой (например, одна расположения возле горнолыжной трассы, а вторая – возле катка, и имеется две группы посетителей – любители горных лыж и конькобежцы).
Решим задачу максимизации прибыли для системы из двух гостиниц, ориентирующихся на цены конкурентов:
[(P1 - 5)q1]’ = 0
[(P2 - 5)q2]’ = 0
Взяв производную, получаем следующие уравнения зависимости между ценами двух гостиниц (реакцию каждой фирмы на цену конкурентов):
(10 - P1/2 + P2/4) - (P1 - 5)/2 = 0;
(10 - P2/2 + P1/4) - (P1 - 5)/2 = 0;
Отсюда имеем кривые реакции в чистом виде:
P1 = (50 + P2) / 4;
P2 = (50 + P1) / 4.
Цены в каждой гостинице идентичны и равны: P1 = P2 = 50 / 3.
Спрос (и предложение) на номера в каждой гостинице совпадает и равно
q1 = q2 = 35/6;
Общий спрос при этом равен QS = 35 / 3.
HHI = (½)2 + (½)2 = 0,5.
Прибыль каждой фирмы равна: p1 = p2 = q1 (P – AC) = (35/6)(50/3 – 5) = 352/18.
Суммарная прибыль pS = p1 + p2 = 352/9.
Пример решения задач к теме 8.
Задача 1.
Модель Форхаймера
Пусть функцию спроса равной P = 40 – Q, функцию затрат фирмы-лидера и фирмы-аутсайдера - С1 =C2=(q1)2 / 2 = (q2) 2/2. Функция отзыва аутсайдера на цену лидера определяется исходя из соотношения MCi = P, а предельные затраты фирм как МС1=q1, MC2=q2, откуда функция реакции второй фирмы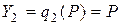 
= q2. Задача фирмы-лидера в этом случае записывается следующим образом:
|
|
|
,
где 
- остаточный спрос для фирмы-лидера.
После дифференцирования данного выражения прибыли по P получаем: P = 15, откуда q2 = 15, qS = 25, q1 = 10, p1 = 100, p2 = 112,5. При этом прибыль фирмы-лидера ниже, чем прибыль последователя, что, однако это компенсируется более высокой рентабельностью.
Задача 2.
Рассмотрим вариант модели Бэйна для ситуации с ограничением производственных мощностей.
Пусть спрос на рынке задан как P = 40 – 2Q, затраты доминирующей фирмы TCD = 4q, при ограничении производственных мощностей KD = 10, а затраты фирм-последователей равны ТСi = 5 при ограничении мощностей Ki = 5.
В данной ситуации возможны две стратегии фирмы-лидера.
Стратегия 1:фирма-лидер устанавливает объем производства qD=KD. При условии, что в качестве конкурентного окружения в отрасли функционирует только одна фирма, суммарный объем производства составил Q = 15, цена P = 10. С вхождением еще одной фирмы произойдет падение цены ниже средних затрат. Однако такая стратегия создает эффект «ценового зонтика» и позволяет фирме-конкуренту развиваться как путем совершенствования технологии, так и путем увеличения мощностей.
Стратегия 2. фирма «допускает» в отрасль двух конкурентов и устанавливает цену на уровне ограничительной: P = 5. При этом спрос на рынке равен 35:2, а остаточный спрос на продукцию доминирующей фирмы - RD = 35:2 – 10 = 15:2 = 7,5. При данной стратегии прибыль уменьшается, однако блокирование вхождения в отрасль новых фирм устраняет угрозу развития фирм конкурентного окружения.
|
|
|
