 |
Базовый уровень Вариант 3. А. Б.2х = –2. В.(х – 1)(х + 3) = 0. Г. A.n = 3pc2. Б. В. Г. Подсказки к заданиям тестов базового уровня
|
|
|
|
Базовый уровень Вариант 3
1. Градусная мера угла  радиан равна ¼
радиан равна ¼
А. 300°. Б. 330°. В. 600°. Г. 150°.
2. Точка тригонометрической окружности с ординатой 1 соответствует числу ¼
А. p. Б.  . В.
. В. 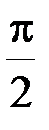 . Г. 0.
. Г. 0.
3. Укажите значение sina, если 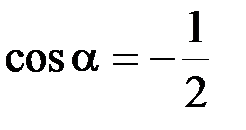 и p < a < 2p.
и p < a < 2p.
А.  . Б.
. Б. 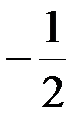 . В.
. В.  . Г.
. Г. 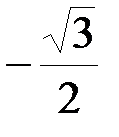 .
.
4. Из данных чисел выберите наибольшее: 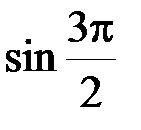 ;
; 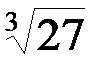 ;
;  ;
;  .
.
А.  . Б.
. Б.  . В.
. В. 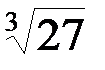 . Г.
. Г.  .
.
5. Вычислите  .
.
А. 2. Б. –2. В. 1. Г. –1.
6. Вычислите  .
.
А. 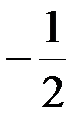 . Б.
. Б.  . В.
. В.  . Г.
. Г. 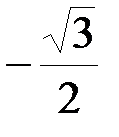 .
.
7. Для всех допустимых значений х выражение (sinx + cosx)2 равно …
А. 1. Б. 1 – 2sin2x. В. 1 + cos2x. Г. 1 + sin2x.
8. Чему равно наибольшее значение выражения sinx + 1?
А. 1. Б.  . В. 0. Г. 2.
. В. 0. Г. 2.
9. Областью определения функции  является множество…
является множество…
А. . Б. . В. . Г. .
 10. На каком рисунке изображен график функции y = –cosx?
10. На каком рисунке изображен график функции y = –cosx?
11.
| y |
| x |
| O |
| –4 |
| –2 |
| –1 |
А. Наибольшее значение функции равно 1.
Б. Функция убывает на промежутке [–2; 2].
В. Функция сохраняет знак на всей области определения.
| y |
| x |
| O |
12. Укажите функцию, график которой схематично изображен на рисунке.
А. y = (0, 5)x. Б. y = 2x. B.  . Г. y = x2.
. Г. y = x2.
13. Ровно один корень имеет уравнение…
А. . Б. 2х = –2. В. (х – 1)(х + 3) = 0. Г. .
14. Решите уравнение  .
.
А. 1. Б.  . В.
. В.  . Г. –1.
. Г. –1.
15. Решите неравенство 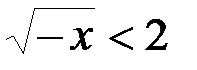 .
.
А. (–¥; 4). Б. [0; 4). В. (–4; 0]. Г. [–2; 0).
16. Из формулы  выразите переменную n через c и p.
выразите переменную n через c и p.
A. n = 3pc2. Б. . В. . Г. .
| y |
| x |
| O |
|
|
|
y = cosx и y = x2. Сколько корней имеет уравнение
cosx = x2 на промежутке (0; +¥ )?
А. Ни одного. Б. Один. В. Два. Г. Три.
18.
| A |
| M |
| N |
| K |
| B |
| D |
| P |
| C |
А. Параллельны. Б. Пересекаются.
В. Скрещиваются. Г. Могут быть расположены как угодно
19. Если две прямые параллельны, то их параллельные проекции на одну плоскость не могут …
А. совпадать. Б. быть параллельными.
В. пересекаться. Г. иметь общие точки.
20. Если две стороны треугольника параллельны некоторой плоскости a, то третья сторона ¼
А. лежит в плоскости a. Б. пересекает плоскость a.
В. параллельна плоскости a.
Г. может пересекать плоскость a, может быть ей параллельна.
21. Прямые а и b параллельны. Сколько плоскостей можно провести через прямую а параллельно прямой b?
А. Ни одной. Б. Одну. В. Ни одной или одну. Г. Бесконечно много.
22. Если плоскость a параллельна прямой b, а прямая b перпендикулярна плоскости b, то плоскости a и b¼
А. параллельны. Б. перпендикулярны. В. параллельны или совпадают.
| A |
| D |
| C |
| B |
| A1 |
| D1 |
| C1 |
| B1 |
23. Дан куб АВСDА1В1С1D1. Чему равен угол между прямыми В1Аи B1D1?
А. 90°. Б. 60°. В. 45°. Г. 30°.
24. Наклонная длиной а составляет с плоскостью проекции угол 45°. Ортогональная проекция этой наклонной на плоскость равна ¼
| A |
| B |
| C |
| D |
| A1 |
| B1 |
| C1 |
| D1 |
 . Б.
. Б.  . В.
. В.  . Г. а.
. Г. а.
| A |
| D |
| C |
| B |
| A1 |
| D1 |
| C1 |
| B1 |
| A |
| D |
| C |
| B |
| A1 |
| D1 |
| C1 |
| B1 |
| A |
| D |
| C |
| B |
| A1 |
| D1 |
| C1 |
| B1 |
| A |
| D |
| C |
| B |
| A1 |
| D1 |
| C1 |
| B1 |
Г. Ответ отличен от приведенных.
|
|
|
Подсказки к заданиям тестов базового уровня
1. Воспользуйтесь следующими соотношениями между градусной и радианной мерами измерениями углов: , 1 рад =.
2. Воспользуйтесь тем, что тригонометрическая окружность — это окружность с центром в начале координат и радиусом, равным 1. Найдите на ней точку с указанной координатой и определите длину дуги, соединяющей эту точку против часовой стрелки с точкой (1; 0). Искомое число и равно полученному значению. Для решения обратной задачи по известной длине указанной дуги найдите координату искомой точки.
3. Воспользуйтесь основным тригонометрическим тождеством
sin2a + cos2a = 1, а по заданному неравенству определите знак искомого значения.
4. Для нахождения наибольшего (наименьшего) значения сравните заданные положительные (отрицательные) числа, например, с 1 (–1).
5. Воспользуйтесь формулами для разности или суммы логарифмов положительных чисел с одинаковыми основаниями и определением логарифма.
Для произвольных положительных а, b, с, a ¹ 1 справедливы равенства:
 ,
,  .
.
|
|
|


