 |
А.(2a)t. Б.a×2t. В.a×(1,02)t. Г.a×1,2t.
|
|
|
|
А. (2a)t. Б. a× 2t. В. a× (1, 02)t. Г. a× 1, 2t.
8. Укажите область определения функции 
.
| y |
| x |
| O |
9. График функции y = ax + b имеет такой вид, как на рисунке, если …
А. a > 1, b > 0. Б. 0 < a < 1, b > 0.
В. a > 1, b < 0. Г. 0 < a < 1, b < 0.
10. Функция 
…
А. нечетна. Б. четна. В. ни четна, ни нечетна. Г. четна при х ³ 0.
11. Найдите сумму корней уравнения 
.
А. –2, 5. Б. –3, 5. В. –3. Г. 0, 5.
12. Укажите все значения параметра b, при которых система уравнений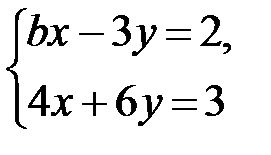 
не имеет решений.
А. b = –2. Б. b = –8. В. b = 2. Г. Таких значений нет.
13. Решите неравенство 
.
А. . Б. Нет решений. В. . Г. .
14. Если сторона и средняя линия трапеции параллельны плоскости a, то плоскости трапеции и a …
А. параллельны. Б. пересекаются.
В. совпадают или параллельны. Г. параллельны или пересекаются.
15. Какие из следующих фигур можно получить как параллельную проекцию прямоугольника 1 дм ´ 2 дм:
I квадрат со стороной 1 дм;
II квадрат со стороной 2 дм;
III прямоугольник 2 дм ´ 3 дм?
А. Ни одну из этих фигур. Б. Только фигуру I.
В. Только фигуры I и II. Г. Все три фигуры.
16. Сечением правильного тетраэдра не может быть …
А. пятиугольник. Б. треугольник. В. прямоугольник. Г. квадрат.
| M |
| A |
| B |
| C |
| О |
А. 60°. Б. 45°. В. 30°. Г. .
18. Точка М находится на расстоянии а от всех вершин равностороннего треугольника АВС со стороной а и центром в точке О. Сравните расстояние d1 от точки М до плоскости АВС и расстояние d2 от точки С до плоскости АОМ.
|
|
|
А. d1 > d2. Б. d1 < d2. В. d1 = d2. Г. Сравнить нельзя.
19. В кубе АВСDA1B1C1D1 проведено сечение плоскостью А1С1D. Сравните величину угла a между этой плоскостью и гранью А1В1С1D1 и угол b сечения.
А. a = b. Б. a < b. В. a > b. Г. Сравнить нельзя.
20. Геометрическим местом точек пространства, равноудалённых от всех сторон трапеции, является …
А. пустое множество. Б. точка. В. прямая.
Г. прямая или пустое множество.
Дополнительное задание
Повышенный уровень
1. Сравните числа 
и 
.
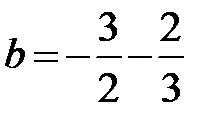А. a = b. Б. a > b. В. a < b. Г. Сравнить нельзя.
2. Упростите выражение 
.
А. 2sin4 + 4. Б. 4. В. cos4 + sin4 + 4. Г. – cos4 + sin4 + 4.
3. Первая цифра после запятой в десятичной записи числа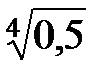 
заключена
в интервале …
А. (5; 8). Б. (8; 10). В. (7; 10). Г. (4; 7).
4. Среди выпускников класса процент медалистов оказался в пределах от
2, 6% до 3, 0%. Каково минимально возможное число выпускников класса?
А. 33. Б. 31. В. 34. Г. 32.
5. Множеством значений функции y = –sina – 6x – 9 –x2 может быть промежуток …
А. (–¥; 1, 7). Б. (1; +¥ ). В. (–¥; 0, 7). Г. (–¥; –2].
6. Укажите все значения параметра а, при которых функция 
нечетна.
А. ±1. Б. 1. В. –1. Г. Таких значений нет.
7. Сумма корней уравнения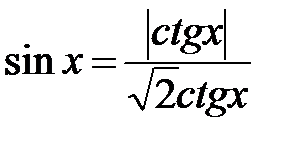 
, лежащих на промежутке [0; 2p],
равна …
А. p. Б. 
. В.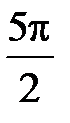 
. Г. 2p.
8. Сколько решений имеет система уравнений 
?
А. Четыре. Б. Шесть. В. Два. Г. Ни одного.
9. Укажите все значения параметра b, при которых неравенство
tg2x – (0, 5)btgx + 1 < 0 не имеет решений.
А. [–1; +¥ ). Б. [1; +¥ ). В. (–¥; –1]. Г. (–¥; 1].
10. Сколько существует двузначных чисел, в 7 раз больших суммы их цифр?
|
|
|
А. Одно. Б. Два. В. Четыре. Г. шесть.
11. Даны две скрещивающиеся прямые а и b и не лежащая на них точка М.
Сколько существует прямых, проходящих через М и пересекающих прямые а и b?
А. Ни одной. Б. Ни одной или одна. В. Одна. Г. Бесконечно много.
12. Найдите расстояние между средней линией грани АВС правильного
тетраэдра DАВС, параллельной ребру ВС, и ребром АD. Ребро тетраэдра равно а.
А. 
. Б. 
. В. 
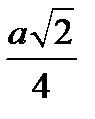. Г.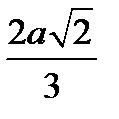 
.
13. Отрезки АВ и А1В1 лежат на скрещивающихся прямых, О и О1 — их
середины. Сравните длину отрезка ОО1 и величину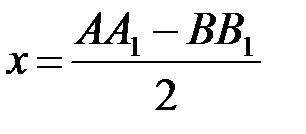 
.
А. ОО1 = х. Б. ОО1 < х. В. ОО1 > х. Г. Сравнить нельзя.
13. В кубе АВСDA1B1C1D1 проведено сечение плоскостью AD1C. Сравните
величину угла a между этой плоскостью и гранью ABCD и угол β = Ð D1AC.
А. a = β. Б. a < β. В. a > β. Г. Сравнить невозможно.
14. Сколько осей симметрии имеет пространственная фигура, состоящая из
двух равных правильных пятиугольных пирамид, вершины которых располо
жены по разные стороны от общего основания, а боковые ребра не равны
ребрам основания?
А. Десять. Б. Шесть. В. Пять. Г. Одну.
15. Дан правильный тетраэдр с ребром 1. Чему равно наибольшее значение
площади ортогональной проекции этого тетраэдра на некоторую плоскость?
А. 0, 5. Б. 1. В. 2. Г. 
.
|
|
|
