 |
Тема 2.4 Дифференциальные уравнения.
|
|
|
|
Тема 2. 4 Дифференциальные уравнения.
Определение дифференциального уравнения. Общее и частное решение дифференциального уравнения. Дифференциальное уравнение I порядка.
Решение задач на составление дифференциальных уравнений. Линейные однородные уравнения. Второго порядка с постоянными коэффициентами.
Практическое занятие: Решение дифференциальных уравнений.
Раздел 3. Теория вероятностей
Определение достоверного и невозможного события, применение аксиом вероятностей при решении задач, вычисление условной вероятности, вычисление вероятности суммы и полная вероятность, вычисление размещений и сочетаний.
Практическое занятие: Вычисление вероятности, условной вероятности, вероятности суммы, полной вероятности, вычисление размещений и сочетаний.
Раздел 4. Математическая статистика
Понятие случайной величины, дискретная и непрерывная случайные величины, закон распределения случайной величины, ряд распределения. Вычисление математического ожидания случайной величины, дисперсии случайной величины, среднего квадратического отклонения случайной величины, построение полигона.
Практическое занятие: Вычисление математического ожидания случайно величины, дисперсии случайной величины, среднего квадратического отклонения случайной величины, построение полигона.
Теоретический материал
Раздел 1. Линейная алгебра
Матрицей размером m× n называется совокупность m·и n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов.
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В. В общем виде матрицу размером m× n записывают так
|
|
|
А= 
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.
Матрица, в которой число строк не равно числу столбцов, называется прямоугольной.
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка А=( 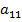
 …
… 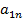 ), называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
), называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например, 0=(0 0 … 0), 0= 
Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
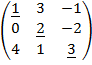
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E.
E= 
Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a11a22–a12a21. Определитель обозначается символом D или |А|или det A.
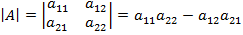
Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
 .
.
Пример: Вычислить определитель третьего порядка.
1. D=  =2
=2 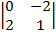 –3
–3  +(–4)
+(–4)  =
=
= 2·(0·1–(–2)·2) – 3(1·1– (–2)·(–2)) –4 (1·2–0·(–1))=8+3–8=3
|
|
|


