 |
Сложение матриц. Умножение матрицы на число. Сложение матриц на примере матриц 3×3 . Обратная матрица. Простейшие матричные уравнения и их решение.
|
|
|
|
Сложение матриц.
Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т. е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Суммой двух матриц A и B называется матрица C, которая определяется по правилу
А+В=  +
+ 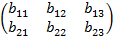 =
= 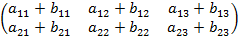
Сложение матриц на примере матриц 3× 3
 +
+ 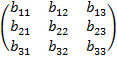 =
= 
- матрицы складываются поэлементно (складываем числа на одинаковых местах)
!!! Складывать можно только матрицы, имеющие одинаковый размер (т. е. одинаковое число строк и столбцов)
Пример: Найти сумму матриц:
-
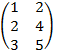 +
+ 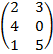 =
= 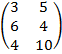 .
. -
 +
+  - нельзя, т. к. размеры матриц различны.
- нельзя, т. к. размеры матриц различны. -
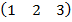 +
+  =
=  .
. -
 +
+  =
= 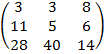 .
.
Транспонирование.
Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером).
A=  B=
B= 
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Пример: Найти матрицу транспонированную данной.
а) A=  ,
, 
б) B= 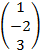 ,
, 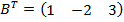 .
.
Умножение матрицы на число.
Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу
k·А =  = k·
= k·  =
= 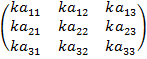
Пример: 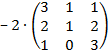 =
= 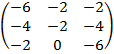 .
.
Умножение матриц.
Произведением матрицы A на матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
|
|
|
 ·
· 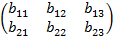 =
= 
Пример: Найти произведение AB, если А=  и В =
и В = 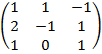 .
.
с11= 3× 1 +1× 2 + 1× 1 = 6 с21= 2× 1 + 1× 2 + 2× 1 = 6 с31= 1× 1 + 2× 2 + 3× 1 = 8
с12= 3× 1 + 1× (-1) + 1× 0 = 2 с22=2× 1 + 1× (-1) + 2× 0 = 1 с32=2× (-1) + 1× 1 + 2× 1 = 1
с13= 3× (-1) + 1× 1 + 1× 1 = -1 с23= 2× (-1) + 1× 1 + 2× 1 = 1 с23= 1× (-1) + 2× 1 + 3× 1 =4
С= 
!!! Матрицы не перестановочны друг с другом, т. е. A∙ B ≠ B∙ A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.
Обратная матрица
Обратной А–1 по отношению к матрице A называется такая матрица, для которой выполняется равенство A·A-1 = A-1·A = E. (Е – единичная матрица).
Для нахождения обратной матрицы используют следующую схему:
1) Находят определитель матрицы А
2) Находят алгебраические дополнения всех элементов матрицы А и записывают новую матрицу
3) Меняют местами столбцы полученной матрицы (транспонируют)
4) Умножают полученную матрицу на 
Пример: Найти обратную матрицу для А=  и выполнить проверку.
и выполнить проверку.
1) Вычисляем D =  = 4
= 4 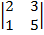 – 1
– 1 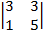 + 4
+ 4 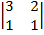 = 20 ≠ 0. следовательно, обратная матрица существует.
= 20 ≠ 0. следовательно, обратная матрица существует.
2) Найдем присоединенную матрицу A*. Для этого вычислим все миноры второго порядка матрицы A и алгебраические дополнения:
А11=(–1)1+1 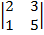 = 7, А21=(–1)2+1
= 7, А21=(–1)2+1  = – 1, А31=(–1)3+1
= – 1, А31=(–1)3+1  = – 5,
= – 5,
А12=(–1)1+2 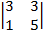 = – 12, А22=(–1)2+2
= – 12, А22=(–1)2+2 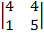 = 16, А32=(–1)3+2
= 16, А32=(–1)3+2  = 0,
= 0,
А13=(–1)1+3 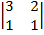 = 1, А23=(–1)2+3
= 1, А23=(–1)2+3 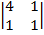 = –3, А33=(–1)3+3
= –3, А33=(–1)3+3  = 5.
= 5.
3) Составим новую матрицу A*=  и транспонируем
и транспонируем
AТ= 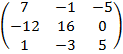
4) Найдем по формуле обратную матрицу:
A-1 =  =
= 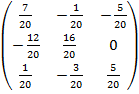
ПроверкаA·A-1 =  ·
· 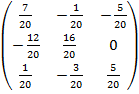 =
=  = Е.
= Е.
Простейшие матричные уравнения и их решение.
Пусть дана система уравнений

Рассмотрим матрицу, составленную из коэффициентов при неизвестных:
А =  .
.
Свободные члены и неизвестные запишем в виде матриц-столбцов
В =  , X =
, X = 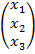 .
.
Тогда матричным уравнением называется уравнение вида А·Х = В.
План решения матричных уравнений:
1) Найти обратную матрицу А–1
2) Найти произведение обратной матрицы А–1 на столбец свободных членов В,
|
|
|
т. е. А–1·В
3) Пользуясь определением равных матриц, записать ответ.
Пример: Решить матричное уравнение  .
.
Составим матричное уравнение А·Х = В: А =  , X =
, X = 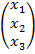 , В =
, В = 
1) Найдем обратную матрицу А–1
Вычислим определитель
D=  =3
=3 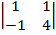 – (–1)
– (–1)  +0
+0  = 3·(4+1)+1·(– 8–2) =5 ≠ 0
= 3·(4+1)+1·(– 8–2) =5 ≠ 0
Запишем все алгебраические дополнения:
А11=(–1)1+1 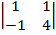 = 5, А21=(–1)2+1
= 5, А21=(–1)2+1 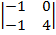 = 4, А31=(–1)3+1
= 4, А31=(–1)3+1  = – 1,
= – 1,
А12=(–1)1+2  = 10, А22=(–1)2+2
= 10, А22=(–1)2+2  = 12, А32=(–1)3+2
= 12, А32=(–1)3+2  = – 3,
= – 3,
А13=(–1)1+3  = 0, А23=(–1)2+3
= 0, А23=(–1)2+3  = 1, А33=(–1)3+3
= 1, А33=(–1)3+3 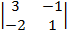 =5.
=5.
Запишем новую матрицу и транспонируем:
А* =  , АТ=
, АТ= 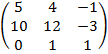
Запишем обратную матрицу: A-1 =  =
= 
2) Х =  ·
·  =
=  =
= 
3) Итак,  , т. е. х1=2, х2=1, х3=3.
, т. е. х1=2, х2=1, х3=3.
|
|
|


