 |
Задание № 1. б) методом Гаусса. Решение типовых примеров. б) методом Гаусса . Решение типового примера
|
|
|
|
Задание № 1
Решение типовых примеров рассмотрено в теоретическом материале*
В задачах 1-10 решить системы уравнений
а) методом Крамера
б) методом Гаусса
№ 1

б) 
в) 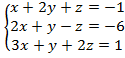
№ 2
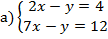
б) 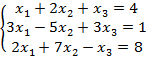
в) 
№ 3
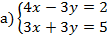
б) 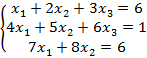
в) 
№ 4

б) 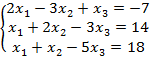
в) 
№ 5
a 
б) 
в) 
№ 6
a 
б) 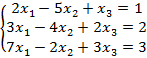
в) 
№ 7
a 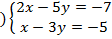
б) 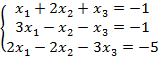
в) 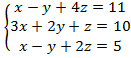
№ 8
a 
б) 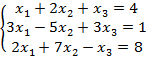
в) 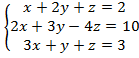
№ 9
a 
б) 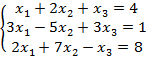
в) 
№ 10
a 
б) 
в) 
Задание № 2
В задачах 11-20 вычислить пределы функции:
11. a) 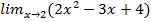 ; б)
; б)  ; в)
; в)  .
.
12. a)  ; б)
; б) 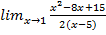 ; в)
; в)  .
.
13. a) 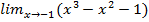 ; б)
; б)  ; в)
; в)  .
.
14. a) 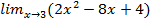 ; б)
; б)  ; в)
; в)  .
.
15. a)  ; б)
; б)  ; в)
; в) 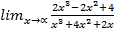 .
.
16. a) 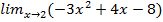 ; б)
; б)  ; в)
; в)  .
.
17. a)  ; б)
; б) 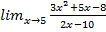 ; в)
; в)  .
.
18. a)  ; б)
; б)  ; в)
; в) 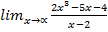 .
.
19. a)  ; б)
; б)  ; в)
; в)  .
.
20. a)  ; б)
; б)  ; в)
; в)  .
.
Решение типовых примеров
Вычислить пределы:
№ 1. 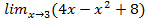
Для нахождения предела данной функции заменим аргумент х его предельным значением 3(выполним непосредственную подстановку):
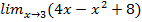 =4·3 – 32+8=12 – 9 + 8=11
=4·3 – 32+8=12 – 9 + 8=11
№2.  =
=  .
.
Непосредственная подстановка приводит к неопределенности типа  . Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и до перехода к пределу сократим дробь на множитель х-2. Числитель – квадратный трехчлен разложим на множители:
. Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и до перехода к пределу сократим дробь на множитель х-2. Числитель – квадратный трехчлен разложим на множители:
2х2 + х – 10 = 0
D = (1)2 – 4·2· (– 10) = 1+80=81 (Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка)
 =
=  = 9
= 9
x1 =  =
=  = 2. х2 =
= 2. х2 = 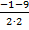 =
= 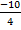 =
= 
2х2 + х – 10 =2 (х-2)(х+  )
)
 =
=  =
=  =
=  =
=  . Ответ:
. Ответ:  .
.
№2. 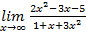
Сначала мы смотрим на числитель и находим х в старшей степени. Старшая степень в числителе равна двум. Теперь смотрим на знаменатель и тоже находим х в старшей степени. Старшая степень знаменателя равна двум. Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке. Итак, метод решения следующий: для того, чтобы раскрыть неопределенность  необходимо разделить числитель и знаменатель на х в старшей степени.
необходимо разделить числитель и знаменатель на х в старшей степени.
|
|
|
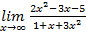 =
=  = (Разделим числитель и знаменатель на х2) =
= (Разделим числитель и знаменатель на х2) =  =
= 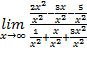 =
= 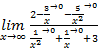 =
=  . Ответ:
. Ответ:  .
.
Задание № 3
В задачах 21-30 исследовать заданную функцию методами дифференциального исчисления и построить эскиз графика. Исследование функций рекомендуется проводить по следующей схеме:
1) Найти область определения функции;
2) Найти производную функции;
3) Найти точки экстремума;
4) Определить промежутки монотонности функции;
5) Найти точки перегиба функции;
6) Определить промежутки выпуклости и вогнутости функции;
7) Найти значение функции в точках экстремума и перегиба;
21. у=2х3–9х2+12х-5
22. у= х3–6 х2+9х +1
23. у=х3–3х2–9х+1
24. у=х3+3х2–9х–10
25. у=х3+6х2+9х+2
26. у=2х3–3х2–12х+5
27. у=2х3+3х2–12х-8
28. у=2х3+9х2+12х+7
29. у=2х3–15х2+36х–32
30. у=2х3–15х2+24х+4
Решение типового примера
Пример: Исследовать и построить график функции у =  х4 –
х4 –  х2.
х2.
1°. Область определения функции - интервал (–∞, ∞ ). Точек разрыва нет.
2°. Здесь f(–x)=f(x), так как х входит только в четных степенях. Следовательно, функция четная и ее график симметричен относительно оси Оу.
3°. Чтобы определить точки пересечения графика с осью ординат, полагаем х = 0, тогда у = 0. Значит, кривая пересекает ось Оу в точке (0; 0).
Чтобы определить точки пересечения графика с осью абсцисс, полагаем у=0:
 х4 –
х4 –  х2 =0; х4–6х2=0; x2(x2–6)=0. Отсюда х2=0, x1, 2=0, т. е. две точки пересечения слились в одну точку касания; кривая в точке (0; 0) касается оси Ох. Далее, имеем х2–6=0, т. е. х3, 4=
х2 =0; х4–6х2=0; x2(x2–6)=0. Отсюда х2=0, x1, 2=0, т. е. две точки пересечения слились в одну точку касания; кривая в точке (0; 0) касается оси Ох. Далее, имеем х2–6=0, т. е. х3, 4=  ≈ ±2, 45. Итак, в начале координат О(0; 0) кривая пересекает ось Оу и касается оси Ох, а в точках А (–2, 45; 0) и В (2, 45; 0) пересекает ось Ох.
≈ ±2, 45. Итак, в начале координат О(0; 0) кривая пересекает ось Оу и касается оси Ох, а в точках А (–2, 45; 0) и В (2, 45; 0) пересекает ось Ох.
4°. Найдем критические точки функции:
|
|
|
y'=x3–3x; x3–3x=0; х(х2–3)=0; х1=0; х2, 3=±  ≈ ±1, 7. Эти точки разбивают область определения функции на интервалы (–∞;
≈ ±1, 7. Эти точки разбивают область определения функции на интервалы (–∞;  ), (
), (  , 0), (0,
, 0), (0,  ), (
), (  , ∞ ).
, ∞ ).
5°. Исследуем критические точки с помощью второй производной.
Находим у" = 3х2 – 3. При х = 0 получим у" х=0=–3, т. е. уmax=0, и, значит, О(0; 0) - точка максимума. Далее при х=  имеем
имеем  = 6, т. е. ymin=
= 6, т. е. ymin=  (
(  )4–
)4–  (
(  )2= –2, 25. Таким образом, D (
)2= –2, 25. Таким образом, D (  ; –2, 25) - точка минимума, а вследствие симметрии минимум достигается также в точке С(-
; –2, 25) - точка минимума, а вследствие симметрии минимум достигается также в точке С(-  ; –2, 25). Составим таблицу:
; –2, 25). Составим таблицу:
| х | (–∞; –  ) )
| – 
| (–  ; 0) ; 0)
| (0;  ) )
| 
| (  ; ∞ ) ; ∞ )
| |
| у' | – | + | – | + | |||
| у | ymin =–2, 25 | уmax=0 | ymin =–2, 25 |
6 °. Имеем у" =3(x2–1) = 0, 3(х–1)(х+1) = 0, х1, 2=±1. Точки х=–1 и х=1 разбивают область определения функции на интервалы (–∞, –1), (–1, 1) и (1, ∞ ). В интервалах (–∞, –1) и (1, ∞ ) имеем у" > 0, т. е. здесь кривая вогнута, а в интервале (–1, 1) имеем у" < 0, т. е. здесь она выпукла. При х= –1 и х= 1 получаем точки перегиба Е и F, ординаты которых одинаковы: у(–1) = у(1)= –1, 25.
Составим таблицу:
| х | (–∞, –1) | –1 | (-1; 1) | (1; ∞ ) | |
| у" | + | – | + | ||
| у | Вогнута | Точка перегиба (–1; –1, 25) | Выпукла | Точка перегиба (1; 1, 25) | Вогнута |
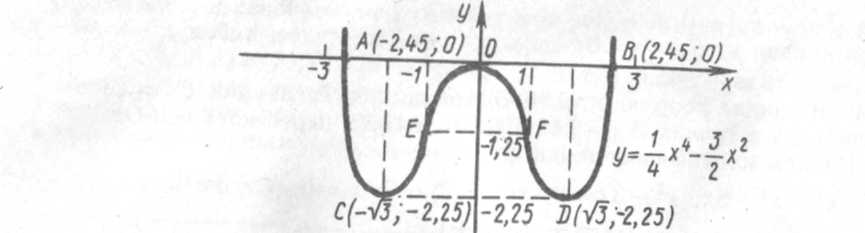
7°. График изображен на рисунке.
|
|
|


