Линейные дифференциальные уравнения 1-го порядка.

Линейные дифференциальные уравнения 1-го порядка.

Дифференциальное уравнение вида 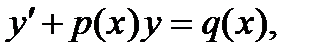где p(x), q(x) – заданные функции, называется линейным дифференциальным уравнением 1-го порядка.

Для решения уравнения воспользуемся способом подстановки. Будем искать неизвестную функцию y в виде y = u(x)v(x). Тогда  Подставим значения y и  в уравнение:

Выберем v(x) так, чтобы выражение в скобках обратилось в нуль, т. е. ,

тогда получится уравнение

Оба уравнения являются дифференциальными уравнениями с разделяющимися переменными. Общее решение исходного уравнения запишется как произведение частного решения уравнения и общего решения уравнения: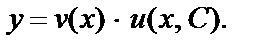

Дифференциальные уравнения 2-го порядка

Дифференциальным уравнением 2-го порядка называется уравнение вида 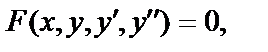где х – независимая переменная, y – неизвестная функция этой переменно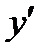й,  и 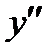 – ее производные.        Общее решение уравнения 2-го порядка имеет вид: y = g(x, C₁, C₂),

где С₁ и С₂ – две произвольные постоянные.

Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

Уравнение 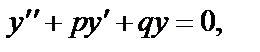где p и q – вещественные числа, называется линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами.

Общее решение уравнения имеет вид: , где у₁ и у₂ – два линейно независимых частных решения этого уравнения, С₁ и С₂ – произвольные постоянные.

Для нахождения линейно независимых частных решений у₁ и у₂ используется характеристическое уравнение вида .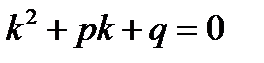

В зависимости от корней характеристического уравнения получаются различные виды функций у₁ и у₂  и вид общего решения уравнения (см таблицу).

 

 

Таблица

Дискриминант характеристического уравнения	Корни характеристического уравнения	Вид общего решения уравнения
	действительные различные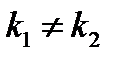
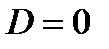
	действительные равные
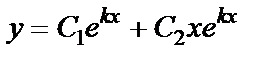
	комплексные

 

Раздел 3. Теория вероятностей

Размещением из n различных элементов по m элементов (m< n) называется соединение, которое отличается либо составом, либо порядком своих элементов. Например, выпишем все размещения из элементов a, b, c, d по два элемента: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc. Для любого натурального числа n произведение 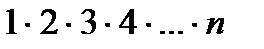 обозначается n! читается n-факториал. Формула для подсчета числа размещений:

Задача: Найти количество всех двузначных чисел, состоящих из чисел 1, 2, 3,..., 9.

Решение: Это задача о размещении из 9 элементов по 2 элемента, т. к. любые двузначные числа отличаются либо составом цифр, либо их порядком.

Сочетанием из n различных элементов по m элементов (m< n) называется соединение, которое отличается только составом своих элементов. Например, выпишем вес сочетания из элементов a, b, c, d, e по три элемента: abe, abd, abe, acd, ace, ade, bcd, bce, bde, cde. Формула для подсчета числа сочетаний:

Задача: Дано 5 различных чисел a, b, c, d, e. Сколько можно составить всевозможных произведений из этих чисел, состоящих из двух различных множителей?

Решение: Это задача о числе сочетаний из 5 элементов по 2 элемента, т. к. произведения отличаются только составом множителей

Перестановками из n различных элементов называются всевозможные соединения из этих n элементов, т. е. соединения, каждое из которых содержит n различных элементов, взятых в определённом порядке. Например, все перестановки из элементов a, b, c: abc, acb, bac, bca, cab, cba. Формула для подсчета числа перестановок: Р_п = n!

Задача: На столе находятся 5 различных геометрических фигур, (круг, треугольник, квадрат, ромб, прямоугольник). Сколькими способами можно разложить эти фигуры в один ряд?

Решение: Это задача о числе перестановок из 5 элементов. Р₅ = 5! = 120.

К основным понятиям теории вероятности относятся: испытание, событие, вероятность. Испытание – реализация комплекса условий, в результате которого непременно произойдет какое-либо событие. Например, бросание монеты – испытание; появление герба или цифры – события. С лучайным событием называется событие, которое при осуществлении испытания может произойти, а может и не произойти. Например, выстрел по цели — это опыт, случайные события в этом опыте – попадание в цель или промах.

Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА. Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С.

Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В. Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.

Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.

Пример. В магазин поступило 40 новых цветных телевизоров, среди которых 7 имеют скрытые дефекты. Наудачу отбирается один телевизор для проверки. Какова вероятность, что он не имеет скрытых дефектов?

Решение: Число телевизоров, не имеющих скрытых дефектов, равно m= 40 − 7 = 33. Число всех элементарных исходов всех поступивших телевизоров равно n= 40. Следовательно, по классическому определению вероятности вероятность того, что отобранный телевизор не имеет скрытых дефектов (событие А), равна P(A)= = = 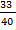0, 825. Ответ: Р(А) = 0, 825.

Условной вероятностью события В  при условии, что событие А произошло, называется отношение вероятности произведения этих событий к вероятности события А, причем Р(А) 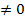 обозначается символом Р(В|А)= Р(АВ)| P(A).

Пример. В урне 2 белых и 7 черных шаров. Из неё последовательно достают два шара. Какова вероятность того, что 2-й шар окажется белым, при условии, что первый шар был чёрным.

Решение: А – 1-й шар черный, В – 2-й шар белый. Т. к. событие А произошло, то в урне осталось 8 шаров, из которых 2 белых шара. Т. о. Р(В|A)=

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: