 |
Формула полной вероятности.. Раздел 4. Математическая статистика
|
|
|
|
Формула полной вероятности.
Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий Н1А, Н2А, ..., HnA. Следовательно,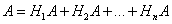 
. Применяя аксиому сложения вероятностей, имеем
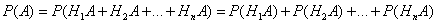
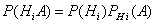(i=1, 2, ..., n), поэтому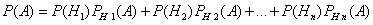 
Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».
Раздел 4. Математическая статистика
Под случайной величиной понимают величину, которая в результате опыта принимает то или иное значение, причем заранее неизвестно, какое именно. Случайные величины обозначают прописными заглавными латинскими буквами: X, Y, Z …, а принимаемые ими значения: x1, x2, …, y1, y2, ….
Пример: 1) Х – число очков, которое появляется при бросании игральной кости.
2) Y – число выстрелов до 1-го попадания в цель.
3) Z – время безотказной работы прибора и т. д.
(Рост человека, курс доллара, прибыль фирмы, выигрыш игрока и т. д. )
Дискретной случайной величиной называется величина, принимающая конечное или счетное множество значений. Непрерывной случайной величиной называется величина, принимающая несчетное множество значений. Случайной величиной Х называется числовая функция, определенная на пространстве элементарных событий Ω, которая каждому элементарному событию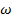 
ставит в соответствие Х( 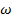), т. е. Х= Х( ), 
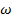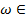Ω ( или Х= 
.
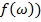Любое правило (таблица, функция, график), позволяющее находить вероятности произвольных событий А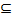 
S (S-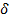 
– алгебра событий пространства Ω ), в частности, указывающее вероятности отдельных значений случайной величины или множества этих значений, называется законом распределения случайной величины.
|
|
|
Закон распределения дискретной случайной величины
Пусть Х – дискретная случайная величина, которая принимает значения х1, х2, …, хn, …, с некоторой вероятностью рi, i = 1, 2, 3, …, n, ….
Закон распределения дискретной случайной величины удобно задавать с помощью формулы рi= Р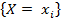 
, i = 1, 2, 3, …, n, ….
Для дискретной случайной величины закон распределения может быть задан в виде таблицы
| Х | х1 | х2 | … | хn |
| Р | р1 | р2 | … | pn |
Таблицу называют рядом распределения.
События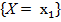 
, 
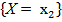… несовместны и образуют полную группу, то сумма их вероятностей равна 1.
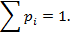
Закон распределения характеризует случайную величину. При решении многих практических задач достаточно знать некоторые числовые параметры, характеризующие отдельные существенные свойства (черты) закона. Такие числа числовыми характеристиками случайной величины.
Важнейшими среди них являются:
- характеристики положения: математическое ожидание (центр распределения случайной величины);
- характеристики рассеяния: дисперсия (отклонение значений случайной величины от ее центра), среднее квадратическое отклонение.
Математическим ожиданием (или средним значением) дискретной случайной величины Х, имеющей закон распределения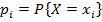 
, i = 1, 2, 3, …n называется число, равное сумме произведений всех ее значений на соответствующие им вероятности.
Математическое ожидание вычисляется по формуле
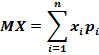
Дисперсией (рассеянием) случайной величины Х называется математическое ожидание квадрата её отклонения от своего математического ожидания. Обозначается дисперсия DX и вычисляется по следующей формуле: 
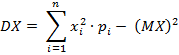
Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии: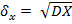 
Из свойств дисперсии вытекают соответствующие свойства среднего квадратического отклонения.
|
|
|
|
|
|
