 |
Задание № 4. Решение типового примера
|
|
|
|
Задание № 4
В задачах 31-40 вычислить неопределенные интегралы, результат проверить дифференцированием.
31. а) 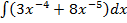 ; б)
; б)  .
.
32. а) 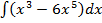 ; б)
; б)  .
.
33. а)  ; б)
; б)  .
.
34. а)  ; б)
; б)  .
.
35. а)  ; б)
; б) 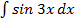 .
.
36. а) 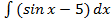 ; б)
; б)  .
.
37. а)  ; б)
; б) 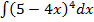 .
.
38. а)  ; б)
; б)  .
.
39. а)  ; б)
; б) 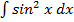 .
.
40. а)  ; б)
; б)  .
.
Решение типового примера
1) Найти неопределенные интегралы, результат проверить дифференцированием.
 =
= 
 +
+ 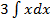
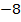
 =
= 
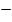
 +
+ 
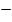 8x + C.
8x + C.
 .
.
Сделаем замену переменной: x² = t. Тогда  . Следовательно,
. Следовательно,
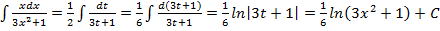 .
.
Задание № 5
В задачах 41-50 вычислить площадь фигуры, ограниченную заданными линиями:
41. у = х2, у = 49.
42. у = х3, у = 8.
43. у = х2+1, х = – 2, х = 2.
44. у = х2, у = 64.
45. у = х+2, х = 2, х = 4.
46. у = х3+1, у = 9.
47. у = х2+1, у = 9.
48. у = 2х, х = 1, х = 2.
49. у = х3+1, у = 28.
50. у = х2+2, у = 27
Решение типового примера.
Вычислить площадь криволинейной трапеции, ограниченной линиями у = 4 - х² и у=0.
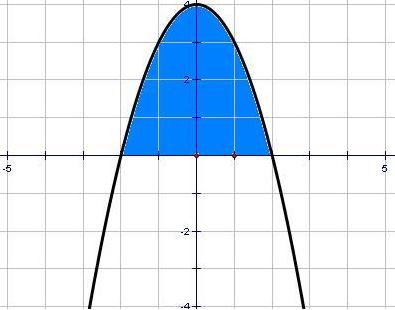 у = 4 – х² - квадратичная функция, график – парабола, ветви направлены вниз, вершина (0; 4)
у = 4 – х² - квадратичная функция, график – парабола, ветви направлены вниз, вершина (0; 4)
у= 0 - ось абсцисс. Найдём точки пересечения параболы с осью х:  ;
; 
Найдем S =  =
=  = – (4·(–2) –
= – (4·(–2) –  ) =
) =  – (–
– (–  ) =
) =  = =10
= =10  (кв. ед).
(кв. ед).
Ответ: 10  кв. ед.
кв. ед.
Задание № 6
В задачах 51-60 найти частное решение дифференциального уравнения первого порядка:
51. 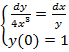 .
.
52. 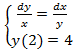 .
.
53. 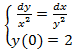 .
.
54.  .
.
55. 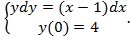
56.  .
.
57. 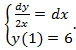
58.  .
.
59.  .
.
60. 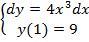 .
.
Решение типового примера
Найти частное решение дифференцированного уравнения первого порядка 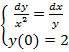 .
.
Это дифференцированное уравнение с разделяющимися переменными.
Производим разделение переменных:
ydy = 2x2 dx
Интегрируя обе части равенства, получаем:
 =
= 
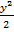 =
= 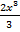 + C
+ C
y2 = 
Используя начальное условие, вычислим, соответствующее ему значение постоянного С:
22 =  ; 2C = 4; C = 2
; 2C = 4; C = 2
Поэтому частное решение исходного дифференцированного уравнения, удовлетворяющее заданному начальному условию, имеет вид: y2 = 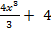 .
.
|
|
|
Задание № 7
Решение типовых примеров рассмотрено в теоретическом материале*
61. В партии 60 изделий, из них 14 c браком. Из партии наугад выбирают 9 изделий. Какова вероятность, что все 9 изделий без брака?
62. В коробке 17 белых 5 жёлтых, 11 зелёных и 8 синих карандашей. Вынимают наугад 4 карандаша. Какова вероятность того, что 1-й жёлтый, 2-й синий, 3-й белый, 4-й зелёный?
63. В коробке 5 белых, 10 синих, 15 чёрных карандашей. Вынимают наугад 3 карандаша, какова вероятность, что 1-й белый, 2-й синий, 3-й чёрный?
64. В коробке 10 белых 15 жёлтых, 13 зелёных и 5 синих карандашей. Вынимают наугад 4 карандаша. Какова вероятность того, что 1-й жёлтый, 2-й синий, 3-й белый, 4-й зелёный?
65. В магазин поступили запчасти для компьютера одного типа, изготовленные на четырех заводах: с 1-го завода 110 шт., со 2-го — 85 шт., с 3-го — 69 шт. и с 4-го — 90 шт. Вероятность того, что запчасть прослужит более гарантийного срока, для 1-го завода равна 0, 4, для 2-го — 0, 33, для 3-го — 0, 45, для 4-го — 0, 18. При раскладке по полкам магазина запчасти были перемешаны. Какова вероятность того, что купленная запчасть прослужит более гарантийного срока?
66. В продажу поступают пылесосы с трех заводов. Продукция первого завода содержит 18 % пылесосов со скрытым дефектом, второго — 12 % и третьего — 6 %. Какова вероятность приобрести исправный пылесос, если в магазин поступило 44 % пылесосов с первого завода, 36 % — со второго и 20 % — с третьего?
67. В 1-м ящике 14 белых и 9 жёлтых шаров, во 2-м 5 жёлтых и 4 белых шара. Вынимают наугад по одному шару из каждого ящика. Какова вероятность того, что оба шара разных цветов?
68. В группе 29 студентов, среди которых 8 отличников. В совет студентов выбирают наугад 7 студентов. Какова вероятность того, что среди отобранных студентов нет отличников?
69. В магазин поступили выключатели одного типа, изготовленные на четырех заводах: с 1-го завода 98 шт., со 2-го — 70 шт., с 3-го — 220 шт. и с 4-го — 180 шт. Вероятность того, что выключатель прослужит менее гарантийного срока, для 1-го завода равна 0, 12, для 2-го — 0, 18, для 3-го — 0, 13, для 4-го — 0, 1. При раскладке по полкам магазина выключатели были перемешаны. Какова вероятность того, что купленный выключатель прослужит менее гарантийного срока?
|
|
|
70. В партии 120 изделий, из них 18% c браком. Из партии наугад выбирают 15 изделий. Какова вероятность, что все 15 изделий с браком?
|
|
|


