Определение неопределённого интеграла

Определение неопределённого интеграла

Пусть f(x) - функция, заданная на объединении интервалов вещественной оси. Набор всех первообразных для f(x) называется неопределённым интегралом от f(x) и обозначается ∫ f(x)dx. Операция нахождения неопределённого интеграла по заданной функции f(x) называется интегрированием этой функции; найти неопределённый интеграл означает проинтегрировать данную функцию. Функция f(x), записанная после знака интеграла (или, как часто говорят, под знаком интеграла), называется подынтегральной функцией.

Согласно доказанным выше теоремам о виде первообразных, неопределённый интеграл от функции f(x) состоит из функций вида F(х)+С, где F(х) - какая-либо фиксированная первообразная для f(x), а С- величина, постоянная на каждом из непересекающихся интервалов, на которых задана функция f(x). Поэтому можно написать такую формулу: ∫ f(x)dx= F(х)+С.

Итак, для того чтобы доказать равенство ∫ f(x)dx= F(х)+С, достаточно проверить, что F(х) - первообразная для f(x), то есть что F′ (х)= f(x).

Таблица неопределённых интегралов

1.		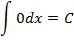9.
2.		10.
3.	, ≠ – 1	11.
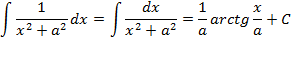
4.		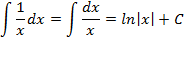12.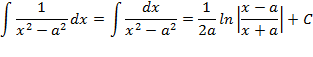
5.		13.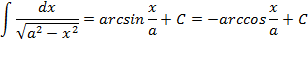
6.		14.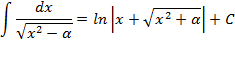
7.		15.
8.		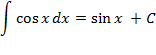16.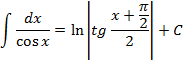

 

Определение определённого интеграла

Для вычисления определенных интегралов от непрерывных функций с конечными пределами необходимо, пользуясь известными методами интегрирования, получить первообразную от интегрируемой функции и, применяя формулу Ньютона-Лейбница 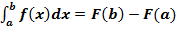, найти разность значений первообразной при подстановке вместо переменной верхнего и нижнего пределов интегрирования.

 

Формула Ньютона–Лейбница: если функция 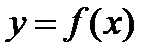 непрерывна на  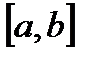и , то имеет место формула: ,      

Свойства определённого интеграла:

  При перемене местами пределов интегрирования знак интеграла меняется на противоположенный

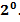 Постоянный множитель подынтегрального выражения можно выносить за знак определённого интеграла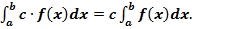

. Определённый интеграл от алгебраической суммы (разности) функций равен сумме (разности) определённых интегралов от каждой функции в отдельности

.

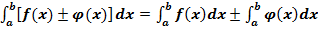Вычисление площади фигуры

Криволинейной трапецией называется фигура, ограниченная прямыми x = a, x= b, y = 0 и кривой . Формула для вычисления площади криволинейной трапеции: .

Тема 2. 4 Дифференциальные уравнения

Дифференциальные уравнения первого поряка

Дифференциальным уравнением 1-го порядка называется уравнение вида

где x – независимая переменная, y – неизвестная функция этой переменной, 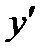 – ее первая производная.

Если уравнение можно разрешить относительно , то его записывают .

Решением дифференциального уравнения называется функция 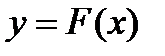 - первообразная для функции 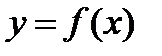, которая при подстановке в дифференциальное уравнение обращает его в тождество. Общее решение дифференциального уравнения 1-го порядка записывается в виде 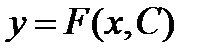, где С – произвольная постоянная.

Задача нахождения частного решения дифференциального уравнения, удовлетворяющего начальному условию, называется задачей Коши. Чтобы найти частное решение дифференциального уравнения, удовлетворяющее начальному условию y(x₀) = y₀, нужно в общее решение уравнения 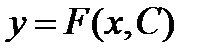подставить x = x₀, y = y₀ и из полученного уравнения найти C, затем найденное значение C подставить в общее решение.

Уравнения с разделяющимися переменными.

Дифференциальное уравнение вида   или

называется дифференциальным уравнением с разделяющимися переменными.

Для того, чтобы решить уравнение, нужно разделить переменные x и y, т. е. собрать в левой и правой его частях функции, зависящие только от одной переменной. Заменим производную  на 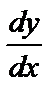 и разделим переменные. Получим: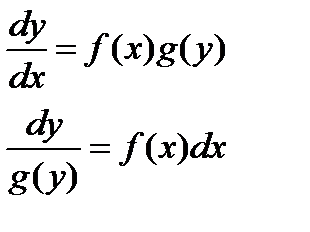

Решение этого уравнения находим почленным интегрированием левой и правой частей:

где С = С₂  – С₁.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: