Главная | Обратная связь | Поможем написать вашу работу!

Учебно-методическое и информационное обеспечение

Задание № 8

Решение типовых примеров рассмотрено в теоретическом материале*

71. а) Дискретная величина задана рядом распределения:

X	-1
P	0. 2	0. 1	0. 4	?

Найти: МХ, DX, .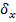

б) Из урны, содержащей 17 шаров (9 синих и 8 желтых), наудачу извлекаются 7 шаров. Рассматривается случай ная величина, значения которой равны количеству желтых шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины, полигон и най ти её математическое ожидание.

72. а) Дискретная величина задана рядом распределения:

X	-1
P	0. 4	0. 1	0. 3	?

Найти: МХ, DX, 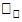и построить полигон.

б) Из урны, содержащей 10 шаров (5 синих и 5 желтых), наудачу извлекаются 4 шара. Рассматривается случай ная величина, значения которой равны количеству желтых шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины и най ти её математическое ожидание.

73. а) Дискретная величина задана рядом распределения:

X
P	0. 05	0. 15	0. 35	?

Найти: МХ, DX, 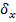и построить полигон.

б)Из урны, содержащей 20 шаров (13 синих и 7 желтых), наудачу извлекаются 6 шаров. Рассматривается случай ная величина, значения которой равны количеству желтых шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины и най ти её математическое ожидание.

74. а)Дискретная величина задана рядом распределения:

X	-1
P	0. 35	0. 25	0. 05	?

Найти: МХ, DX, 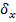и построить полигон.

б)Из урны, содержащей 17 шаров (10 синих и 7 желтых), наудачу извлекаются 8 шаров. Рассматривается случай ная величина, значения которой равны количеству синих шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины и най ти её математическое ожидание.

75. а) Дискретная величина задана рядом распределения:

X
P	0. 4	0. 3	0. 1	?

Найти: МХ, DX, 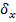и построить полигон.

б) Из урны, содержащей 18 шаров (9 синих и 9 желтых), наудачу извлекаются 6 шаров. Рассматривается случай ная величина, значения которой равны количеству желтых шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины и най ти её математическое ожидание.

76. а) Дискретная величина задана рядом распределения:

X
P	0. 2	0. 2	0. 4	?

Найти: МХ, DX, 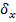и построить полигон.

б) Из урны, содержащей 17 шаров (10 синих и 7 желтых), наудачу извлекаются 5 шаров. Рассматривается случай ная величина, значения которой равны количеству синих шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины и най ти её математическое ожидание.

77. а) Дискретная величина задана рядом распределения:

X
P	0. 33	0. 17	0. 3	?

Найти: МХ, DX, 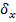и построить полигон.

б) Из урны, содержащей 19 шаров (11 синих и 8 желтых), наудачу извлекаются 7 шаров. Рассматривается случай ная величина, значения которой равны количеству синих шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины и най ти её математическое ожидание.

78. а) Дискретная величина задана рядом распределения:

X
P	?	0. 3	0. 4	0. 2

Найти: МХ, DX, 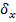и построить полигон.

б) Из урны, содержащей 10 шаров (6 синих и 4 желтых), наудачу извлекаются 4 шара. Рассматривается случай ная величина, значения которой равны количеству синих шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины, най ти её математическое ожидание.

79. а) Дискретная величина задана рядом распределения:

X	-1
P	0. 2	?	0. 1	0. 5

Найти: МХ, DX, .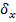

б) Из урны, содержащей 11 шаров (5синих и 6 желтых), наудачу извлекаются 5 шаров. Рассматривается случай ная величина, значения которой равны количеству желтых шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины, полигон и най ти её математическое ожидание.

80. а) Дискретная величина задана рядом распределения:

X	-1
P	0. 4	0. 1	?	0. 2

Найти: МХ, DX, 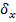и построить полигон.

б) Из урны, содержащей 10 шаров (4 синих и 6 желтых), наудачу извлекаются 4 шара. Рассматривается случай ная величина, значения которой равны количеству синих шаров, оказавшихся среди извлеченных шаров. Построить закон распределения этой случай ной величины и най ти её математическое ожидание.

Учебно-методическое и информационное обеспечение

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы

Основные источники:

1. Богомолов, Н. В. Математика: учеб. для ссузов. - М.: Дрофа, 2006. - 395 с.

2. Богомолов, Н. В. Практические занятия по математике. - М.: Высш. шк., 2002. - 495 с.

3. Валуцэ, И. И. Математика для техникумов. – М.: Наука. Гл. ред. Физ. мат. лит., 1990 – 576 с.: ил.

4. Кочетков, Е. С. Теория вероятностей и математическая статистика /Учебник для студентов учреждений среднего профессионального образования / Е. С. Кочетков, С. О. Смерчинская, В. В. Соколов: -2-е изд. -М.: Форум, 2008-240с. -(Профессиональное образование).

5. Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А. А. Дадаян. – М. Форум, 2011. - 544 с. - (Профессиональное образование).

6. Математика: Учебное пособие для студентов образовательных учреждений сред. проф. образования/ В. П. Омельченко, Э. В. Курбатова. – 3-е изд., испр. – Ростов н/Д: Феникс, 2008. – 380 с. - (Среднее профессиональное образование).

7. Математика: учебное пособие для студентов средних специальных учебных заведений/ Н. А. Березина, Е. Л. Максина. – М.: РИОР, 2007. – 175 с. – (Профессиональное образование).

8. Соловейчик, И. Л. Сборник задач по математике с решениями для техникумов. - М.: ООО " Издательский дом " ОНИКС 21 век", 2003. - 464 с.

9. Лисичкин В. Т., Соловейчик И. Л. Математика в задачах с решениями: Учебное пособие. 3-е изд. стер. - СПб.: Издательство «Лань», 2011.

Дополнительные источники:

1. Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В. «Алгебра и начала анализа (10-11 кл. )». - М.: Просвещение, 2007.

2. Григорьев В. П., Дубинский Ю. А. «Сборник задач по высшей математики»: учебник для студ. учреждений сред. проф. образования – М.: Академия, 2010.

3. Григорьев В. П., Дубинский Ю. А. «Элементы высшей математики»: учебник для студ. учреждений сред. проф. образования – М.: Академия, 2008.

4. Данко, П. Е., Попов А. Г., Кожевникова, Т. Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. 1: Учеб. Пособие для втузов. – 7-ое изд., испр. – М.: Высш. шк., 2009 – 448 с.: ил.

5. Данко, П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. 2: Учеб. Пособие для втузов. – 7-ое изд., испр. – М.: Высш. шк., 2009. – 416 с.: ил.

6. Письменный, Д. Т. Конспект лекций по высшей математике. 1 часть. – 3-е изд. – М.: Айрис –пресс, 2009. – 288 с.: ил.

7. Максимова, О. В. Теория вероятностей и математическая статистика: Учебное пособие для студентов учреждений среднего профессионального образования / О. В. Максимова, А. М. Махоткина - Ростов н/Д: Феникс, 2008- 347с. (Среднее профессиональное образование).

8. Кочетков, Е. С. Теория вероятностей в задачах и упражнениях: Учебное пособие для студентов вузов / Е. С. Кочетков, С. О. Смерчинская: -2-е изд. -М.: Форум, 2011-480с. -(Высшее образование).

⇐ Предыдущая 3 4 5 6 7 8 9 101112 Следующая ⇒

Воспользуйтесь поиском по сайту: