 |
Подсказки к заданиям повышенного уровня
|
|
|
|
Подсказки к заданиям повышенного уровня
1. Представьте данные дроби в виде 1 ± а, где а — правильная дробь с числителем, равным 1, и сравните вначале значения а для всех дробей, пользуясь следующим правилом сравнения дробей с равными числителями.
Из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше.
Из двух дробей с одинаковыми числителями меньше та, знаменатель которой больше.
2. Обратите внимание на то, что среди сомножителей есть число, заканчивающееся цифрой 5, и чётное число.
3. Не ошибитесь при установлении указанных чисел.
4. Обратите внимание на то, что из двух неравных натуральных чисел правее на координатном луче, расположенном горизонтально и направленном слева направо, изображается точкой большее число.
5. Выразите равные числа через данные и запишите соответствующее равенство. Преобразуйте это равенство так, чтобы можно было сравнить данные числа.
6. Обратите внимание на то, что в задании известно, как изменились сумма двух значений величины и одно из слагаемых. Проанализируйте, как изменилось второе слагаемое.
7. В заданиях рассматриваются два значения величины, равной произведению значений двух других величин. Можно ввести обозначения для сомножителей одного значения, выразить через них сомножители второго значения и оба произведения.
8. Обратите внимание на то, что у двух пар чисел равные знаменатели.
9. Вначале найдите, чему равна заданная дробь от данного числа, а потом подсчитайте число, дробь от которого найдена.
10. В задании можно найти два значения величины по их сумме и отношению. Для их нахождения можно составить уравнение или воспользоваться методом решения задачи на части.
|
|
|
11. Найдите вначале расстояние по известным скорости и времени, а затем искомую скорость по известным расстоянию и времени.
12. Можно составить уравнение, выбрав в качестве неизвестного длину всего пути (или массу всего зерна, или стоимость всего товара в магазине).
13. Воспользуйтесь тем, что если сложить почленно все заданные равенства, то получим удвоенный или утроенный периметр треугольника. Искомую разность можно выразить из найденного периметра треугольника и заданных равенств.
14. Разбейте данную фигуру на части, площади которых вы можете найти, и воспользуйтесь свойством площади:
Если фигура разделена на несколько фигур, не имеющих общих частей, то её площадь равна сумме площадей этих фигур.
Установите вначале путём построений, какому из данных чисел может быть равна длина основания равнобедренного треугольника.
Углубленный уровень Вариант 1
1. Мальчик, перемножив два двузначных числа, получил трехзначное число с одинаковыми цифрами. Сложив эти же числа, он получил двузначное число также с одинаковыми цифрами. Сколько существует пар таких чисел?
А. 1. Б. 2. В. 3. Г. 4.
2. В записи 
цифры заменены буквами. Разным цифрам соответствуют разные буквы, одинаковым цифрам — одинаковые буквы. Чему равна сумма а + b + c?
А. 11. Б. 14. В. 16. Г. 12.
3. Если на одну чашку весов положить кирпич, то для равновесия на вторую чашку придется положить гирю в 1 кг и полкирпича. Сколько весит кирпич?
А. 1 кг. Б. 1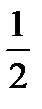 
кг. В. 2 кг. Г. 3 кг.
4. Какой цифрой заканчивается произведение 50 семерок?
А. 1. Б. 3. В. 9. Г. 7.
5. Из 4х цифр, ни одна из которых не равна нулю, составили наибольшее и наименьшее четырехзначное числа. Их сумма оказалась равной 11220. Чему равна сумма всех данных цифр?
А. 6. Б. 20. В. 21. Г. 22.
|
|
|
6. В коробке лежат 15 шариков: черных, белых и красных. Красных в семь раз меньше, чем белых. На сколько больше в коробке черных шариков, чем красных?
А. На 1. Б. На 7. В. На 12. Г. На 6.
7. Кузнечик прыгает по прямой большими и малыми прыжками. Большой составляет 12 см, малый 7 см. За какое наименьшее число прыжков он попадет из А в В, расстояние между которыми равно 3 см?
А. За 12. Б. За 4. В. За 6. Г. За 5.
8. В коробке лежат 100 карандашей одинаковых по форме и размерам, но разных по цвету: красные, синие, зеленые, коричневые, черные. Какое наименьшее количество карандашей надо взять, чтобы среди них было хотя бы 6 карандашей одного цвета?
А. 25. Б. 26. В. 30. Г. 36.
9. Детское домино составлено из пустой картинки, а также из картинок, на которых изображены кенгуру, обезьяна и сова. Сколько всего костей содержит это домино?
А. 8. Б. 10. В. 6. Г. 15.
10. В классе 25 человек. Трое из них не занимается ни гимнастикой, ни легкой атлетикой, 12 человек занимается гимнастикой, 16 – легкой атлетикой. Сколько человек занимается и гимнастикой, и легкой атлетикой?
А. 3. Б. 5. В. 6. Г. 9.
|
|
|
