Передаточная функция(коэффициент передачи).

Введение

Сигналы управления и возмущения в общем случае могут быть не детерминированные, а случайные, поэтому приходиться прибегать к статистическим методам исследования систем автоматического управления (САУ). Кроме того, часть объектов функционирует и работает в конфликтных ситуациях. Рассмотрим график изменения выходного вектора САУ во времени (рис.2.)

где у* — желаемая траектория объекта управления.
В начальный момент гп система находилась в точке А. При включении системы управления выходная координата у под действием управляющих сигналов выходит на требуемую (желаемую) траекторию у*.
Разность E(t)=y*(t)-y(t) называется ошибкой или рассогласованием САУ.
задача теории автоматического управления (ТАУ) состоит:

1. Научиться проектировать системы управления, обеспечивающие минимальные допустимые для данного объекта ошибки E(t);
2. проектировать системы управления, которые обеспечивают выход системы на желаемую траекторию за минимальное время, т.е. решается задача быстродействия соответствующим выбором системы управления.

Итак, в самом общем случае САУ, выполняющая поставленные выше задачи, может быть представлена в виде блок-схемы (рис.З)

На вход управляющего устройства (УУ) поступает:

1. задающее воздействие g;
2. информация о текущем состоянии объекта в виде выходной величины у;
3. информация о действующем на ОУ возмущении F.

УУ вырабатывает, в соответствии с полученной информацией, определенное (по заданному алгоритму) управляющее воздействие и на объект. В свою очередь УУ в общем случае состоит из:

- чувствительного устройства (ЧУ);
- вычислительного устройства (ВУ);
- исполнительного устройства (ИУ).

Чувствительное устройство (измерительные устройства, датчики) служат для измерения и преобразования подаваемых на УУ воздействий g, у, F. Вычислительное устройство реализует алгоритм работы УУ. В простейших случаях оно осуществляет простые математические операции, такие как сравнения, т.е. разность g-y-F, операции интегрирования и т.п. В более сложных случаях вычислительное устройство может представлять собой ЭВМ, и даже комплекс ЭВМ. Исполнительные устройства предназначены для непосредственного управления ОУ. Например, для согласования мощности ВУ и ОУ необходимо применить усилитель мощности. В тех случаях, когда ИУ отсутствует, САУ называется прямого регулирования. При наличии ИУ САУ называется непрямого регулирования.

Лекция №2

Математическое описание автоматической системы управления.

Дифференциальное уравнение.

Система или устройство x(t)-вход, y(t)- выход. В большинстве случаев при описании используется дифференциальное уравнение. Правая часть содержит производные входа, левая часть производные выхода.

m, n – порядок управления, чаще всего так говорят про число n.

Пример 1.

 

Операторное представление.

Преобразования Лапласа.


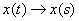
- оригинал.
- изображение.
Применим преобразования Лапласа к заданному дифференциальному уравнению при нулевых начальных условиях, в результате получим.

s- комплексная переменная
x,y-функции от s.

Передаточная функция(коэффициент передачи).

Отношение изображения выходного сигнала к изображению входного сигала, при нулевых начальных условиях, называется передаточной функцией. Пусть объект описывается уравнением, применим к нему преобразования Лапласа.


- передаточная функция.
Пример:

Найти коэффициент передачи.

Моделирование динамических объектов(систем).

найти решение -->

Утверждение: Системы уравнений могут быть смоделированы при помощи трех функциональных блоков.
-сумматор
-усилитель
–интегратор
Пример:

Смоделировать устройство которое описывается этим уравнением.
Переходим к изображению




Принципиальная схема:

Лекция №3

Характеристики динамических систем:

1. Временные.
2. Частотные.

Временное устройство
U(t)=1 или u(t)=1(t) – на вход подается единичный сигнал.
выходной сигнал h(t) – переходной функцией называется реакция на единичную ступень.
Если перейти к изображению.
y(s)=w(s)u(s)

s-комплексная переменная.
- изображение переходной функции равно изображению передаточной функции деленное на s.
Импульсная переходная функция(весовая функция).
Называется реакция системы на импульс.
- реакция системы на импульс.
- дельта импульс.



Основная характеристика дельта импульса:

высота дельта импульса стремиться к
ширина дельта импульса стремиться к 0
S=1
Рассмотрим связь между двумя временными характеристиками и их изображением.

Пример:
Апериодическое звено.

- связь между изображением переходной функции и изображением импульсной переходной функцией.
Интеграл от импульсной переходной функции есть переходная функция. Реальное дифференцирующее звено.

Лекция №4

При исследовании и создании САУ, аппарат частотных характеристик был одним из первых, т.к они наиболее полно отражают физическую природу процессов, происходящих в динамических объектах.
В качестве преобразования функции f(t) используется преобразование Фурье

Преобразование Фурье позволяет разложить непериодическую функцию f(t) для которой выполняется условие сходимости

в бесконечный ряд гармоник, образующих непрерывный спектр частот в интервале от до с бесконечно малым интервалом частот между смежными частотами ( 0).
Отметим, что по сравнению с преобразованием Лапласа преобразование Фурье позволяет отобразить оригинал только на мнимую ось, в преобразовании Лапласа же используется вся комплексная плоскость.
Для перехода к частотным характеристикам, необходимо в уравнение ПФ (3) вместо оператора Лапласа p подставить оператор Фурье , получим частотную характеристику

(3)

Рассмотрим понятие о частотных характеристиках.
Если на вход линейной разомкнутой системы (или звена) подать гармонический входной сигнал, то по истечении некоторого времени окончания переходных процессов на выходе системы (звена) установится также гармонический выходной сигнал той же частоты. Амплитуда и фаза при прочих равных условиях будут зависеть от частоты входного сигнала. По ним, как будет показано дальше, можно судить о свойствах САУ.

Достоинством частотных методов является то, что частотные характеристики можно снять экспериментально. Чтобы снять частотную характеристику необходимо на вход подавать гармонический сигнал, изменяя частоту от 0 до , а на выходе измерять амплитуду и фазу для частот w_i,.
Отметим еще, что в выражении передаточной функции и частотной характеристики для реальных систем степень знаменателя всегда больше степени числителя n>m, т.к. полоса пропускания частот реальной системы всегда ограничена. Действительно, если n<m, то на выходе системы при увеличении частоты могут возникнуть колебания с бесконечно большой амплитудой.
Частотная характеристика (ЧХ) элемента или системы может быть представлена в двух видах:

1. 
2. 

• - вещественно-частотная характеристика (ВЧХ);
• - мнимо-частотная характеристика (МЧХ);
• - амплитудно-частотная характеристика (АЧХ);
• - фазо-частотная характеристика (ФЧХ).

Часто ЧХ представляется графически (рис.1) на комплексной плоскости, где все указанные величины связаны между собой по следующим соотношениям.

Часто при исследовании систем используются логарифмические частотные характеристики.

123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: