Понятие о логарифмических частотных характеристиках

При исследовании САУ, амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это связано с двумя обстоятельствами:

1. в логарифмических масштабах кривизна характеристик резко уменьшается, что позволяет в большинстве практических случаев приближенно изображать АЧХ ломаными линиями
2. в логарифмических масштабах АЧХ цепочки звеньев равна сумме АЧХ отдельных звеньев

АЧХ в логарифмических масштабах строится в координатах и а ФЧХ - в виде зависимости от . Единицей измерения служит децибел, равная 0,1 бела. Бел - единица измерения десятичного логарифма коэффициента усиления мощности сигнала, т.е. 1 бел соответствует усилению мощности в 10 раз, 2 бела - в 100 раз и т.д. Так как мощность сигнала пропорциональна квадрату амплитуды А²
(Пример: для электрической цепи ). 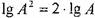, то усиление в белах, выраженное через отношение амплитуд A, равно , соответственно в децибелах оно равно

По оси абсцисс откладывается в логарифмическом масштабе частот (десятичный логарифм)(изменение частоты в 10 раз - декада), а около отметок указывается само значение частоты. Иногда По оси абсцисс откладывается в логарифмическом масштабе частота (десятичный логарифм) (изменение частоты в 10 раз - декада), а около отметок указывается само значение частоты. Иногда применяется логарифм частоты при основании 2 (изменение частоты в два раза - октава) одна октава разно 0,303 декады, т.к. lg2 = 0,303.

Для построения логарифмических фазовых характеристик (ЛФХ) на оси абсцисс используется аналогичная шкала частот или , а по оси ординат (обычно используется нижняя часть плоскости) откладывается фаза в градусах.

Отметим ещё, т.к. точка 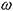=0 в логарифмическом масштабе находится слева, то ЛАФХ строятся не от 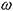=0, а от достаточно малого, но конечного значения 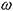, которое и откладывается в начале координат

Лекция №5

Усиливающее звено.

1. Безынерционное звено, сигнал на выходе которого, строго пропорционален сигналу на входе, называется усилительным звеном (рис.1).
По определению
g(t) - входное воздействие (один из стандартных сигналов),
x(t) -реакция на выходе, коэффициент пропорциональности.

2.Переходя к преобразованию Лапласа , тогда передаточная функция:
к - коэффициент усиления (если величинабезразмерная) и коэффициент передачи (если 6 размерно).

3.1. Если на вход усилительного звена подать единичную ступенчатую функцию g(t), то переходная функция будет иметь вид, как показано на рис.2.

3.2. Для получения импульсной переходной функции необходимо продифференцировать по времени переходную характеристику, тогда на выходе имеем -функцию.
3.3. Частотная характеристика
3.3.1.

на комплексной плоскости имеет вид:

3.3.2. ЛЧХ:


ЛФХ:
Описание реальных элементов динамическими характеристиками усилительного безинерционного звена является всегда некоторой идеализацией, т.к. все реальные объекты в природе - инерционны.

Интегрирующее звено.

Звено сигнал на выходе которго пропорционален интегралу сигнала на выходе называется интегрирующим звеном.
По определению:


2. Из свойства преобразования Лапласа:
Тогда по определению передаточная функция будет

Отметим, что коэффициент передачи интегрирующего эвена имеет размерность 1/сек.
3.1. Если - единичная ступенчатая функция, то переходная функция интегрирующего звена имеет вид (рис.6).
3.2. Если , то, дифференцируя ,получим (рис.6).
3.3. Частотная характеристика.
3.3.1.

т.е. амплитудно-фазовая характеристика при изменении частоты от 0 до «э проходит по отрицательной мнимой оси комплексной плоскости (рис.7).

33.2. ЛАХ:
Вычислим значение ЛАХ при и

Следовательно, при изменении частоты на 1 декаду, амплитуда уменьшается на 20 децибел (рис.8).

ЛФХ: