 |
Тема.1 Импульсный элемент (идеальный)
|
|
|
|
п.0. Введение
Рассмотрим систему управления в вычислительным устройством в УУ:

Ранее мы предполагали, что период квантования достаточно маленький и дискретностью по времени
можно пренебречь. Например, если наименьшая постоянная (инерционность) больше периода квантования, например
больше на 2 порядка, то дискретностью по времени можно пренебречь.
УУ включает в себя алгоритм вычисления и вносит дискретность по времени, т.е. УУ можно представить так:

Алгоритм “отнесем” к объекту (непрерывная часть), тогда система управления + объект может быть зарисована в виде такой системы:

где ИЭ – импульсный элемент.
Допустим:

 - период квантования, импульсы определенной формы модулируемые сигналом.
- период квантования, импульсы определенной формы модулируемые сигналом.
Примечание: “Хвосты” импульсов могут накладываться:

---- - 
Хвосты могут тянуться долго, они меняют вид сигнала. Как правило будем считать,
что импульсный элемент генерирует прямоугольные импульсы.

 - период квантования
- период квантования

п.1. Эквивалентная схема импульсного элемента
Схема импульсного элемента:

Его эквивалентная схема

ИИЭ – идеальный импульсный элемент, ФЗ – формирующее
звено. Эта схема должна функционировать эквивалентно одному квадрату.
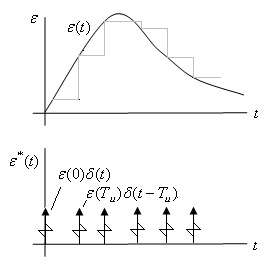
Последовательность модулированных  - импульсов.
- импульсов.

 - формирует прямоугольные импульсы.
- формирует прямоугольные импульсы.
 (изображение по Лапласу).
(изображение по Лапласу).
Известно:



Итак, получим:  .
.

Таким образом система с вычислителем может быть преобразована к такой структуре:

НЧ – непрерывная часть (там находятся объект и алгоритм счета),
 - формирование из
- формирование из  - импульса прямоугольный импульс,
- импульса прямоугольный импульс,
ИИЭ – идеальный импульсный элемент (выдает последовательность
 - импульсов),
- импульсов),
 - приведенной непрерывной части.
- приведенной непрерывной части.
Задачи для экзамена
|
|
|
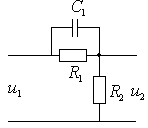
№ 5
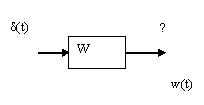
Прикладывается некоторое напряжение, необходимо найти передаточную
функцию W и все ее характеристики.
№ 6
Дано:  . Синтез по L (известны σ и tпп)
. Синтез по L (известны σ и tпп)
№ 7
Дано:  . Синтез по L (известны σ и tпп)
. Синтез по L (известны σ и tпп)
№ 8
Дано:  . Алгебраический синтез.
. Алгебраический синтез.
№ 9
Дано:  .Требуется нарисовать L и φ (диаграмму Bode)
.Требуется нарисовать L и φ (диаграмму Bode)
№ 10
Необходимо написать передаточную функцию W и нарисовать L.

п.2. Изображение дискретного сигнала
Последовательность модулируемых  - импульсов:
- импульсов:
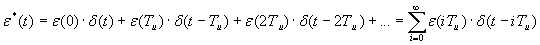
Примечание:
 , * - признак что сигнал дискретный.
, * - признак что сигнал дискретный.
Изображение дискретного сигнала: 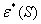

 .
.
Иногда: 

 (обозначают через Z), Z – сдвиг по времени на такт вперед
(обозначают через Z), Z – сдвиг по времени на такт вперед
(тоже самое, как нет оператора дифференцирования - физически). Т.е. правую часть можно записать так:
 - изображение дискретного сигнала по переменной Z.
- изображение дискретного сигнала по переменной Z.
Если Z – сдвиг по времени на такт вперед, то 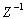 - запаздывание на такт.
- запаздывание на такт.
Генератор импульсов:

Лекция №21
(п.2. Изображение дискретных сигналов)
* - признак дискретного по времени сигнал.

последовательность δ- импульсов сдвинутых по времени iTu и модулированных сигналом X(t) cоотв.значением Х(iTu).
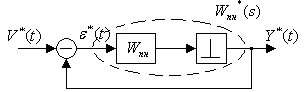
п.3. Передаточная функция импульсной системы

Найдем передаточную функцию этой системы(связь между изображением входа и выхода). Звено ИИЭ перенесем налево:

a δ(t) –b δ(t) = (a-b) δ(t)
Структурное преобразование эквивалентно:
V Y ε
a δ(t) –b δ(t) = (a-b) δ(t)
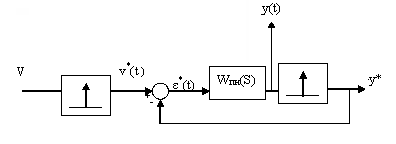

Будем искать передаточную функцию между 2-мя точками.
Зная связь между V*(t)>-->Y*(t) легко восстановить связь между V(t)-->Y(t)(но для дискретных моментов времени).


На рис.5а последовательность δ(t)- импульсов это ε*(t).
импульсная переходная ф-ия
Нас интересует реакция системы в момент времени t, который лежит в пределах l* Tu ≤ t ≤ (l + 1)* Tu. Нужно рассмотреть воздействие импульсов приложенных на тактах 0, 1, …l(будущее не влияет на настоящие).
Система линейная, справедлив принцип суперпозиции, т.е. реакция системы будет равна сумме реакций. Будем брать t в дискретные моменты Tu.
|
|
|
Формулы:

Комментарий(к *):
Предел вверху l можно заменить на 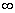 .
.
t < 0 => ωпн(t) = 0, т.к. на будущее воздействие системы не реагирует.
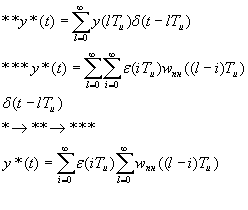
Введем 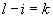 :
:


Лекция №22
(Передаточная функция импульсной системы)

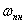 - импульсная переходная функция.
- импульсная переходная функция.
Переход к изображениям:

Известно, что: 

Сделаем преобразование:
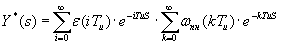


Дискретная передаточная функция: 



Примечание: Допустим дано выражение:
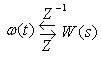
 , сумели представить в виде
, сумели представить в виде
ряда, где 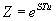 . То тогда
. То тогда 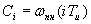 - дискретное значение переходной характеристики передаточной функции.
- дискретное значение переходной характеристики передаточной функции.
Если дана импульсная переходная характеристика
п.4. Передаточная функция замкнутой дискретной системы


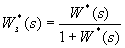 .
.
Исключаем  получаем большое выражение и находим связь между
получаем большое выражение и находим связь между 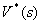 и
и  .
.
Пример 1: Дано: 
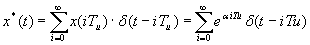
 =
=
Обозначим  , то получим убывающую геометрическую прогрессию.
, то получим убывающую геометрическую прогрессию.
=  , где Z
, где Z  .
.
Z – краткое обозначение оператора сдвига по времени на такт вперед.
Примечание:
 - звено (оператор) запаздывания на такт. Можно строить структуры содержащие звено
- звено (оператор) запаздывания на такт. Можно строить структуры содержащие звено
запаздывания  . В дискретных системах
. В дискретных системах  играет туже роль, что интегратор в непрерывных системах.
играет туже роль, что интегратор в непрерывных системах.
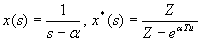 .
.
Получили сопоставления изображения непрерывного и дискретного изображения.
п.5. Устойчивость дискретных систем
Пусть дано:  - передаточная функция замкнутой дискретной системы
- передаточная функция замкнутой дискретной системы

Лекция №23


k*,A* - полиномы от Z.

(*) – ХПЗС.
Для устойчивости все его корни должны лежать в левой полуплоскости плоскости С.
Но полином функция от 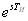 , S=j(w+wn)+α – комплексная переменная. Можно показать, что экспонента функция периодическая с периодом по мнимой оси. Период
, S=j(w+wn)+α – комплексная переменная. Можно показать, что экспонента функция периодическая с периодом по мнимой оси. Период
WИ=2П/ТИ

Для устойчивости необходимо и достаточно, чтобы корни ХПЗС лежали в левой половине полосы.
От S --> Z:
Легко показать, что при переходе от S к Z левая полуплоскость на плоскости Z отобразится в единичную окружность.

Для устойчивости (**) корни должны лежать в единичном круге, т.е. по модулю быть меньше 1.(если лежит на единичной окружности, то на границе устойчивости).
Введем переменную: V= z-1/z+1.
В новой переменной внутренность единичного круга отображается в левую полуплоскость плоскости V.

Вывод:  сделав цепочку преобразований Sà Zà V получаем ХПЗС переменной V, применяем критерии из непрерывной теории.
сделав цепочку преобразований Sà Zà V получаем ХПЗС переменной V, применяем критерии из непрерывной теории.
|
|
|
Дано: Требуется исследовать замкнутую систему на устойчивость
Т1 – инерционность.
ТИ – период квантования.
К – коэффициент усиления.
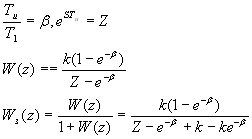
Будем исследовать систему по Гурвицу. Берем ХПЗС:

Необходимо и достаточно чтобы система была устойчивой.


Область устойчивости.
Лекция №24
(Передаточная функция замкнутой дискретной системы)
Передаточная функции замкнутых дискретных систем – есть отношение полиномов от 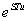 .
.
 , при
, при  .
.
Делим левую часть (числитель и знаменатель) на  . Тогда получим следующее выражение:
. Тогда получим следующее выражение:
 .
.
Преобразуем далее:
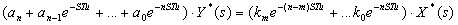 ,
,

Переходим к оригиналам:
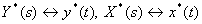 ,
, 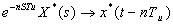
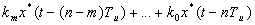
Возьмем  , где
, где  - целое. Тогда:
- целое. Тогда: 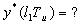 ,
,  . Итак, получим:
. Итак, получим:
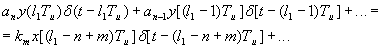
Получили дискретное соотношение вх/вых, необходимо избавиться от  .
.
Проинтегрируем уравнение по времени  .
.
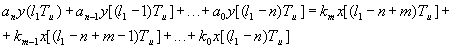
Обозначим 

 и подставим, получим следующее выражение:
и подставим, получим следующее выражение:
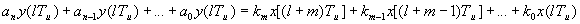
|
|
|


