 |
Тема. 6 Пространство состояний (ABCD )
|
|
|
|
п.0. Введение
Здесь есть 3 дифференциальных уравнения 1-го порядка.
(A,B,C,D) – четверка матриц.
Лекция №16
Пример: Синтез по логарифмическим характеристикам.
Известно: 
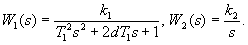
Требуется сделать систему устойчивой и чтобы выполнялись требования к качеству переходного процесса.
1) Строим ЛАЧХ исходной (Lнск) системы. Для этого необходимо убрать обратную связь и посмотреть
По формальному правилу построения L. Найдем 
. Необходимо отметить точку 20lg k = 20lg 50 = 34. В данной системе 2 звена: интегратор и колебательное звено. 
, lg 40 = 1,6.
Возможные варианты решения:
1 вариант
2 вариант
Для 1 варианта:
Для 2 варианта:
Продолжение примера прошлой лекции:
x1, x2, x3 – выходы динамических звеньев.
Опишем данную структуру системой уравнений:
, 
.
,
.
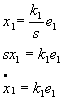
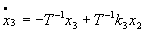Желательно алгебраические уравнения исключить.
Эти 3 дифференциальных уравнения можно записать в виде:
(1) 
x, y, u(t) – функции от времени t
, 
, где A =, 
, 
.
Описание системы в виде (1) называется описанием системы в пространстве состояний.
Дифференциальное уравнение (1):
Описание системы в виде (1) может быть кратко задано так:
nхn nх1 1хn
(A, b, c)
А в более общем виде:
nхn nхm mхn
(A, B, C)
n – размерность матрицы А, размерность вектора x.
m – число входов и число выходов в системе.
По (1) легко найти передаточную функцию. Для этого переходим к изображениям (при нулевых начальных условиях):
x, y, u (s) – функции от s.
.
Лекция №17
(пространство состояний)
п.1. Понятие пространства состояний
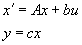
, где Х – вектор состояний.
С = 1x2 строка.
b = 2x1 столбец.
число входов
A nxn
b nx1
C1xn
число выходов
n - размерность вектора состояний Х.
п.2. Управляемость, наблюдаемость
Пример 1:
не управляемый блок схемы.
|
|
|
, где 
какое-то число.
Система не управляемая(см. пример) т.е. нет возможности сочинить алгоритм управления такой, что вектор состояний будет управляемый.
Примечание:
- Если система не управляемая, то можно выделить управляемую и не управляемую часть.
- Если не управляемая часть неустойчивая, то система неработоспособна при любом алгоритме управления.
Пример 2:
(*)- матрица наблюдаемости.
rangθ=n - наблюдаемая система, иначе нет.
rangθ=1 - система ненаблюдаемая.
Примечание:
- Если система ненаблюдаемая, то можно выделить ненаблюдаемую и наблюдаемую части.
- Если ненаблюдаемая часть неустойчивая, то не существует алгоритма управления обеспечивающего устойчивость системы.
Утверждение:
Возможны любые сочетания свойств управляемости и наблюдаемости (лучше всего управляемая и наблюдаемая; неплохо если неуправляемые и ненаблюдаемые части устойчивые)
Пример 3:
Система управляемая, но ненаблюдаемая.
Лекция №18
п.3. Синтез.
Пусть дано описание объекта в пространстве состояний.
, где b – вектор-столбец, с – вектор-строка
Пусть доступен для управления вектор состояния x. Требуется найти алгоритм управления такой, чтобы система имела заданный желаемый ХП (характеристический полином).
Вне штриховой лини – устройство управления.
Передаточная функция объекта:
Корни (полюса), полюса характеризуют устойчивость (неустойчивость), качество переходных процессов.
Пример: Пусть первое уравнение имеет вид:
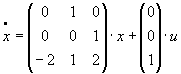Как найти ХП?
Необходимо взять 
. Если матрица А размером 3 х 3, тогда det (определитель) матрицы 
будет полином 3-ей степени.
,
- ХП объекта (т.е. полином знаменателя передаточной функции). Исследуем объект на устойчивость по Гурвицу, объект неустойчивый (т.к. в ХП есть отрицательные коэффициенты при S).
#
Система: 
Найдем описание с учетом УУ, а именно подставим u в 
:
, где:
bp – матрица размером n x n, rang (bp) = 1 (потому что она является произведением 2-х матриц, каждая из которых имеет ранг 1).
|
|
|
С учетом УУ система преобразовалась к виду: 
ХПЗС = 
, т.е. система: 
+ регулятор + обратная связь. A, b – известно, при помощи p добьемся чего-нибудь.
Задача: Необходимо сделать УУ такое, чтобы имел полюса равные -3, -3, -3. Т.е. ХПЗС 
.
, rang (bp) = 1.
Выписываем А:
Блочная матрица:
В примере матрица А задана в каноническом виде, последняя строка - это коэффициенты ХМ матрицы с “перевернутым” знаком: 
.
Подставляем: 
, отсюда мы можем легко найти 
. 
. #
Примечание 1:
(размышление об РГЗ)
Пружина с гирькой без демпфирования описывается таким уравнением: 
.
Описание в пространстве состояний: 
.
, 
.
Ab
Для реализации выше изложенного алгоритма нам необходим вектор X, т.е. компонента 
- это y, т.е. координата грузика. И компонента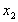 
- скорость. Нужен 
, т.е. нам нужны 2 датчика: положения и скорости.
Примечание 2: Алгоритм решения простой, из-за специального вида матриц A и b. В общем случае матрица A не канонического вида.
Примечание 3: Если матрица А задана в произвольном виде, то переходим к другому базису 
, где Т – преобразование подобия.
х – вектор в старом базисе, 
- вектор в новом базисе.
Тогда берем 1-ое уравнение: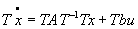 
, получим 
. От матрицы А перешли к матрице 
- это подобное преобразование матриц, свойства не меняются, так получают каноническую форму.
Лекция №19
|
|
|
