Формулировка критерия устойчивости Nyquista.

Предположение – разомкнутая система устойчивая.

Для того, чтобы замкнутая система была устойчивой, годограф разомкнутой системы не должен охватывать точку (-1, j0).

Пример 1:

Пусть , (k,t >0)

замкнутая система устойчива.

Пример 2:

k, k1, k2 >0

T > 0, 0< d < 1.

Очевидно, что 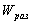- устойчивая система, т.е. попали в условия формулировки.

 

1) Устойчивая система

2) На границе устойчивости

3) Неустойчивая

При увеличении годограф “раздувается”.

2 вар. d – уменьшаем

d4<d3<d2<d1

1) Замкнутая система устойчивая

2) Если , то система приближается к границе устойчивости.

Пусть: разомкнутая система неустойчивая, а замкнутая система – устойчивая.

Пусть у D справа r – корней и замкнутая система устойчивая.

Если у разомкнутой системы справа r корней, то W повернется на или в положительном направлении.

Лекция №11

Примечание:

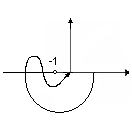
годограф не охватывает -1, значит система устойчивая.

разомкнутая – устойчивая, замкнутая – неустойчивая.

четверть окр. бесконечно

большого радиуса.

Это построение (см выше)равносильно замене интегратора апериодическим звеном, с постоянной стремящейся к 0.

Если, то нужно добавить 2 четверти окружности(пол окружности) обход по часовой стрелке.

Пример:

Дано:

Найти: такое k чтобы система была устойчивой.

Дополненный годограф охватывает критическую точку, следовательно, система неустойчивая.

Вывод: при помощи k систему сделать устойчивой нельзя!

п.3. Устойчивость по логарифмическим характеристикам.

(Диаграммы Bode, или логарифмический аналог критерия устойчивости Nyquista)

Пусть объект имеет вид:

,где k,t,d (0,1)

d1>d2>d3

при d = 0.

Замкнутая система находится на границе устойчивости, т.е. незначительные изменения параметров объекта могут сделать систему как устойчивой так и неустойчивой.

По рисунку нарисуем диаграммы bode:

устойчивая
правило: если сначала w1, а потом w2, то система устойчивая;

если наоборот, то неустойчивая.

Система неустойчивая.

Лекция №12

Точность в установившемся режиме.
п.0. Вывод основных коэффициентов передачи.

V – задание (программа),

Y – выход системы или регулируемая величина,

Е – ошибка или рассогласование,

- коэффициент передачи разомкнутой системы,

F – возмущение (мешает системе)

- коэффициент передачи по возмущению.

Задача: Проанализировать точность системы установившемся режиме.

Внимание в данной лекции K -...

Найдем изображение выходного сигнала, как функцию двух входов V,F.

Пусть: F ≡ 0.

.

Другая ситуация: V ≡ 0.

Тогда, преобразуем к виду типовых соединений:

.

Итоговая формула:

В идеале: , .

Выразим формулу ошибки:

Пусть: F ≡ 0.

Другая ситуация: V ≡ 0

.

Итоговая формула ошибки:

Желательно: .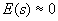

п.1. Входной сигнал – константа.

Найдем соотношения, связывающие параметры W со значениями задающих воздействий.

.

?Можно ли найти .

= .

Случай 1: не содержит интегратора.

где: K - полином от s без свободного члена.

Тогда: .

Полином + полином без свободных = полином без свободных.

.

.

Найдем формулу ошибки в установившемся режиме:

где - коэффициент усиления разомкнутой системы,

- коэффициент передачи(усиления) по возмущению.

Пример: . Разомкнутая система не содержит интегратора.

Требуется найти .

Остается: .

Коэффициент усиления разомкнутой системы должен быть ≥ 19 (для уменьшения ошибки в установившемся режиме необходимо увеличивать коэффициент усиления разомкнутой системы).

Случай 2: содержит интегратор.

.

Для того, чтобы ошибка была равна 0 в установившемся режиме при const на входе, в УУ необходимо ввести интегратор.

Лекция №13

Точность в установившемся режиме
п.2.Линейно нарастающие сигналы.

Рассмотрим систему:

Выражение ошибки системы:

E(S) =

- без интегратора.

- содержит интегратор.

P>Случай 1:

W0 объекта не содержит интегратора.

Линейнонарастающая функция.

С течением времени ошибка растет неограниченно, т.е. такая система с течением времени работает все хуже и хуже.

Случай 2:

W0 содержит интегратор.

Если W0 содержит интегратор, то для линейно возрастающего сигнала, ошибка пропорциональна V0 и обратно пропорциональна K0, т.е. чтобы уменьшить ошибку необходимо увеличить K0.

п.3.Синусоидальный сигнал на входе.

A=1

φ=0

w – задана.

На выходе будет синусоида, амплитуда и фаза которой определяется комплексным числом W(jw) для заданного w.

Например для апериодического звена

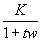
K,t – заданные числа.

Подставим w и для него получилось такое число:

Для случая F = 0

Тема. 5 Синтез УУ по логарифмическим характеристикам.

Пример: (см. лекцию №11)

Используем:

критерий Nyqista:

Дополненный годограф охватывает (-1;jw), следовательно система неустойчивая.

Критерий Михайлова:

ХПЗС:

Годографы Михалова, случай устойчивой системы.

n- степень ХПЗС.

Отсюда находим w* и подставляем.

Гурвиц: система неустойчивая т.к. среди коэффициентов ХПЗС есть 0.

Лекция №14 п.0. Вводные замечания. В начале: УУ – нет. Для системы у которое нет УУ, есть О построим диаграмму Bode (L,?). Если диаграмма Bode выглядит следующим образом, то система устойчивая. В некоторых случаях О → Б → не устойчивая => необходимо ввести УУ. Видимо УУ должна скорректировать “----” до непрерывной линии. , . Пример: Выразить по графику W. . Пример: Взяли . Система может быть устойчивой не удовлетворяющая по качеству переходного процесса – или длинный переходный процесс, или большие колебания, тогда нужно ввести УУ. 20 lg k = 20 lg 100 = 40. 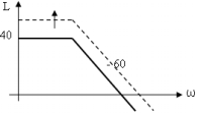Если k ↑, то диаграмма поднимается вверх => неустойчивое состояние. Изменением k можно добиться не только устойчивости, но видимо, заданного качества системы. Можно “доказать”, что должна пересекать ось частот с наклоном: – 20. Перерегулирование σ тем больше, чем меньше участок h.. Коррекция системы – это “насилие” над системой. Поэтому нужно корректировать систему, как можно меньшей полосе частот. п.1.Диаграммы зависимости (запас устойчивости по амплитуде и фазе) - частота среза - запас устойчивости по амплитуде (отражает перерегулирование) - время переходного процесса. Чем L1 больше, тем перерегулирование σ меньше. Чем больше , тем время переходных процессов меньше. Допустим необходимо, чтобы σ? 30%. Тогда то L1 ≥ 10, φ≈400. ωп - полоса положительности. ωср» 0,8 ωп. . На частоте среза: |W(jω)| = 1 (на меньших частотах |W(jω)| > 1). На частотах больше частоты среза идет ослабление сигнала. Допустим нам нужно . Пример: Пусть нам дано РГЗ, обрезанное с 2-х концов: . Найти УУ такое, чтобы: См. выше: L1» 10, » 30. lg 30» 1.7.

Лекция №15

(синтез по логарифмическим характеристикам)

п.2. Сопряжение L желаемой с L нескорректированной.

Рис.1.

L нск (см. формальное правило построения L)

Найти: w ср -?Если дано: t пп = 0,7; = 30%.

t пп =4.7П / w п

w ср = 08w п

Получена среднечастотная часть L ск. Нужно достроить L ск в области низких и высоких частот.

Руководствуемся принципом минимального вмешательства в частотные характеристики объекта. На НЧ и ВЧ совпадает L ск с L нск.

Примечание:

1. штриховые участки можно менять на 20% – 30% с целью упрощения алгебраического регулятора.(корректора).
2. возможны принципиально отличные варианты:

Рис.2. Рис.3.

На средних и высоких частотах мы увеличиваем коэффициент передачи нашей системы, т.е. на средних и высоких частотах мы форсируем систему.

1. правее от w ср – форсируем, левее – давим.

п.3. Построение L корректора (регулятора).

L нск. на графиках представляется в 2-х вариантах:

L – точная,

L – аппроксимирующая.

По рис.1:

По рис.2:

По рис.3:

Примечание:(область применения)

Wраз.нск не должна содержать нулей и плюсов.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: