 |
Первообразная и ее основные свойства
|
|
|
|
С. В. Хасанов, Т. Т. Кузбеков, С. Е. Сысоев
ИНТЕГРАЛ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПРАКТИКУМ
Уфа 2015
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Уфимский государственный авиационный технический университет»
С. В. Хасанов, Т. Т. Кузбеков, С. Е. Сысоев
ИНТЕГРАЛ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПРАКТИКУМ
Допущено Редакционно-издательским советом УГАТУ
в качестве практикума для студентов технических направлений
заочной формы обучения
Уфа 2015
УДК 517(07)
ББК 22.16я7
Х24
 Рецензенты:
Рецензенты:
в.н.с. Института математики с вычислительным центром УНЦ РАН, д-р физ.-мат. наук Мукминов Ф. Х.;
зав. кафедрой математики и статистики БГПУ им. М. Акмуллы, д-р
физ.-мат. наук, проф. Гадыльшин Р. Р.
Хасанов, С. В.
Х24 Интеграл. Дифференциальные уравнения: практикум / С. В. Хасанов, Т. Т.Кузбеков, С. Е. Сысоев; Уфимск. гос. авиац. техн. ун-т. – Уфа: Уфимск. гос. авиац. техн. ун-т, 2015. – 109 с.
ISBN
Практикум охватывает разделы “Интегральное исчисление и обыкновенные дифференциальные уравнения” дисциплины “Математика”, изучаемые на технических направлениях заочной формы обучения. Содержит необходимые теоретические сведения о методах вычисления интегралов и решения дифференциальных уравнений первого и высших порядков, примеры решения типовых задач и 30 вариантов заданий для выполнения расчетно-графической работы.
Практикум предназначен для студентов заочной формы обучения, выполняющих расчетно-графическую работу по дисциплине “Математика”.
|
|
|
Научный редактор: д-р физ.-мат. наук, профессор Булгакова Г. Т.
УДК 517(07)
ББК 22.16я7
ISBN © Уфимский государственный
авиационный технический университет, 2015
Оглавление
Введение ……………………………….................................................... 5
1. Неопределенный интеграл ……………………….............................. 6
1.1. Первообразная и ее основные свойства ……………………..…… 6
1.2. Неопределенный интеграл и его основные свойства ……............. 7
1.3. Задачи для самостоятельного решения …………………............... 9
1.4. Замена переменной в неопределенном интеграле ………............. 9
1.5. Задачи для самостоятельного решения ….…......………….......... 10
1.6. Интегрирование по частям в неопределенном интеграле........... 10
1.7. Задачи для самостоятельного решения......................................... 12
1.8. Интегрирование рациональных дробей........................................ 12
1.9. Задачи для самостоятельного решения ….…............................… 18
1.10. Интегрирование тригонометрических функций........................ 18
1.11. Задачи для самостоятельного решения ………........................... 21
1.12. Интегрирование дробно-линейных иррациональностей........... 21
1.13. Задачи для самостоятельного решения …….…......…………… 22
1.14. Интегрирование квадратичных иррациональностей................. 22
1.15. Задачи для самостоятельного решения …….…......…………… 24
2. Определенный интеграл ….....….....……………………….............. 25
2.1. Определенный интеграл и его свойства...............……………......25
2.2. Вычисление интеграла с помощью
формулы Ньютона-Лейбница ……………………………………. 26
2.3. Задачи для самостоятельного решения......................................... 27
2.4. Замена переменной в определенном интеграле........................... 28
2.5. Задачи для самостоятельного решения ……….………….…....... 29
2.6. Интегрирование по частям в определенном интеграле............... 30
2.7. Задачи для самостоятельного решения ….………….………....... 31
3. Несобственные интегралы................................................................. 32
|
|
|
3.1. Интегралы с бесконечными пределами
(интегралы 1-го рода)...................................................................... 32
3.2. Задачи для самостоятельного решения ……….……………........ 33
3.3. Интегралы от неограниченных функций
(интегралы 2-го рода)...................................................................... 33
3.4. Задачи для самостоятельного решения ………………................. 35
4. Геометрические приложения определенного интеграла …............ 36
4.1. Площадь плоской фигуры.............................................................. 36
4.2. Задачи для самостоятельного решения ……....……..................... 38
4.3. Длина дуги плоской кривой ……................................................... 39
4.4. Задачи для самостоятельного решения ………............................. 41
4.5. Объем тела вращения...................................................................... 41
4.6. Задачи для самостоятельного решения …………………….…… 42
5. Двойной интеграл............................................................................... 43
5.1. Двойной интеграл и его приложения............................................ 43
5.2. Задачи для самостоятельного решения ………………..………... 48
5.3. Замена переменных в двойном интеграле.................................... 49
5.4. Задачи для самостоятельного решения......................................... 52
6. Криволинейный интеграл первого рода........................................... 53
6.1. Криволинейный интеграл первого рода и его приложения........ 53
6.2. Задачи для самостоятельного решения ….......….......................... 56
7. Дифференциальные уравнения первого порядка............................ 57
7.1. Основные понятия об уравнениях первого порядка.................... 57
7.2. Уравнения с разделяющимися переменными............................... 58
7.3. Задачи для самостоятельного решения ………............................. 59
7.4. Однородные уравнения первого порядка..................................... 59
7.5. Задачи для самостоятельного решения ………………………..... 60
7.6. Линейные уравнения первого порядка.......................................... 60
7.7. Задачи для самостоятельного решения ………………………..... 62
7.8. Уравнения в полных дифференциалах.......................................... 62
7.9. Задачи для самостоятельного решения ……………………......... 64
8. Дифференциальные уравнения высших порядков.......................... 65
8.1. Основные понятия об уравнениях высших порядков.................. 65
8.2. Уравнения, допускающие понижение порядка............................ 66
8.3. Задачи для самостоятельного решения ………......…................... 70
8.4. Линейные однородные уравнения с постоянными
|
|
|
коэффициентами ………………………………………………….. 70
8.5. Задачи для самостоятельного решения ….....…............................ 72
8.6. Линейные неоднородные уравнения с постоянными
коэффициентами и специальной правой частью …...................... 72
8.7. Задачи для самостоятельного решения.….................................... 77
9. Домашнее задание.............................................................................. 78
9.1. Основные правила и требования................................................... 78
9.2. Варианты задания............................................................................ 78
Список литературы.............................................................................. 109
ВВЕДЕНИЕ
В учебном пособии рассматриваются разделы “Интегральное исчисление функции одной переменной, двойные интегралы, криволинейные интегралы первого рода и обыкновенные дифференциальные уравнения” дисциплины “Математика”, изучаемые во втором семестре на технических специальностях заочной формы обучения. Оно предназначено для студентов, выполняющих расчетно-графическую работу по интегральному исчислению и обыкновенным дифференциальным уравнениям. Приведенные краткие теоретические сведения, типовые задачи и примеры по каждому разделу позволяют успешно справиться с аналогичными заданиями самостоятельно и способствуют формированию предметного представления о соотношении теоретических и практических результатов.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Первообразная и ее основные свойства
Определение. Функция  называется первообразной функции
называется первообразной функции 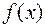 , заданной на (a; b), если
, заданной на (a; b), если 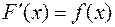 для всех
для всех 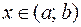 .
.
Например, функции 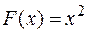 и
и 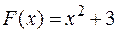 являются первообразными для
являются первообразными для  .
.
Следующая теорема говорит, что первообразные одной функции могут отличаться только на константу.
Теорема. Если  – первообразная функции f (x), то любая другая ее первообразная
– первообразная функции f (x), то любая другая ее первообразная 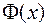 имеет вид
имеет вид  , где
, где  – некоторая постоянная.
– некоторая постоянная.
Сгеометрической точки зрения множество первообразных представляет совокупность (семейство) кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т. е. вдоль оси Оу.
|
|
|
Определение. Если  – одна из первообразных функции
– одна из первообразных функции 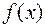 , то
, то 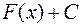 , где
, где  – произвольная постоянная, называется неопределенным интегралом от функции
– произвольная постоянная, называется неопределенным интегралом от функции 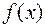 :
:

При этом функцию 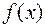 называют подынтегральной функцией
называют подынтегральной функцией 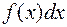 – подынтегральным выражением, знак ∫ – знаком интеграла.
– подынтегральным выражением, знак ∫ – знаком интеграла.
Таким образом, неопределенный интеграл представляет собой семейство функций 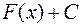 .
.
Для всякой ли функции 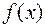 существуют первообразные (а значит, и неопределенный интеграл)? Не для всякой. Но оказывается, что если функция
существуют первообразные (а значит, и неопределенный интеграл)? Не для всякой. Но оказывается, что если функция 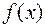 непрерывна на отрезке [ a; b ], то для этой функции существует первообразная (а значит, и неопределенный интеграл).
непрерывна на отрезке [ a; b ], то для этой функции существует первообразная (а значит, и неопределенный интеграл).
Выяснению методов, с помощью которых находятся первообразные (и неопределенные интегралы) от некоторых классов элементарных функций, посвящена настоящая глава.
|
|
|


