 |
Линейные неоднородные уравнения с постоянными коэффициентами и специальной правой частью
|
|
|
|
Рассмотрим линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами
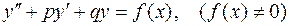, (8.18)
где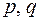 
– действительные числа.
Общее решение этого уравнения записывается в виде 
, где 
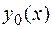– общее решение соответствующего однородного уравнения (8.13), 
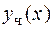– любое частное решение уравнения (8.18). Общее решение ОДУ (8.13) 
. Нахождение 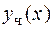рассмотрим в двух частных случаях, когда правая часть уравнения (8.18) имеет вид 
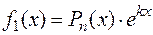, где 
– многочлен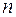 
-й степени, 
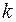– действительное число, или 
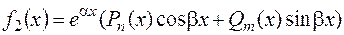, где 
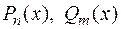– многочлены степен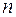и и 
, соответственно, 
– действительные числа. В этих двух случаях частное решение 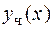можно найти методом неопределенных коэффициентов.
Пусть правая часть имеет вид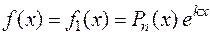 
. Если 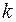не совпадает ни с одним корнем характеристического уравнения, то частное решение 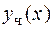ищется в виде
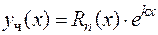, (8.19)
где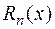 
– многочлен той же степени, что и , но с неопределенными коэффициентами, которые надо найти. Для чего, вычисляя с помощью (8.19)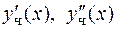 
и подставляя в исходное уравнение (8.18), сокращаем правую и левую части на 
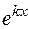. Приравнивая коэффициенты при одинаковых степенях 
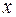, получим систему уравнений для отыскания неопределенных коэффициентов. Подставив их в (8.19), будем иметь искомое частное решение .
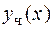Если 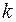совпадает с некоторым корнем характеристического уравнения кратности 
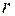, то частное решение ищется в виде
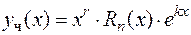. (8.20)
Дальнейшие действия аналогичны предыдущему случаю.
Пусть теперь правая часть уравнения (8.18) имеет вид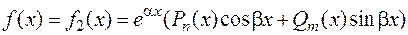 
.
Если число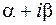 
не совпадает ни с одним из корней характеристического уравнения, то частное решение ищется в виде
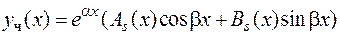, (8.21)
где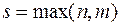 
, 
и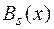 
– многочлены одной и той же степени 
, но с разными неопределенными коэффициентами, которые находятся так же как и в первом случае.
Если 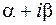совпадает с некоторым корнем характеристического уравнения кратности 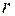, то частное решение ищется в виде
|
|
|
, (8.22)
где , , 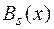те же, что и выше.
Замечание. Если в правой части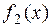 
один из многочленов или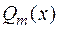 
– нулевой (т.е. 
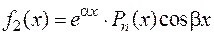или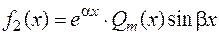 
), то вид частного решения не меняется, т.е. 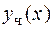ищется в форме (8.21) или (8.22).
Пример 1. Найти общее решение уравнения 
.
Решение. Общее решение уравнения ищется в виде 
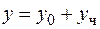. Характеристическое уравнение 
имеет корни 
. Общее решение соответствующего однородного уравнения есть 
.
Правая часть неоднородного уравнения 
, где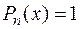 
, откуда 
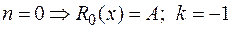совпадает с одним корнем характеристического уравнения 
, следовательно, по формуле (8.20) частное решение имеет вид: 
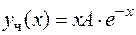, где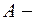 
неопределенный коэффициент. Найдем его методом неопределенных коэффициентов, для чего, подставив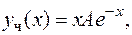 
, 
в исходное уравнение, будем иметь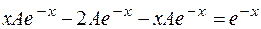 
. Сократим последнее уравнение на 
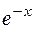, получим 
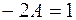. Приравняем коэффициенты при одинаковых степенях
.
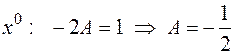Так как неопределенный коэффициент найден, 
, то частное решение имеет вид: 
, следовательно, общее решение исходного уравнения запишется в форме:
.
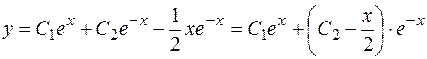Пример 2. Найти общее решение уравнения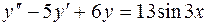 
.
Решение. Уравнение 
это уравнение с правой частью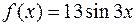 
второго типа, его общее решение ищется в виде .
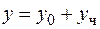Характеристическое уравнение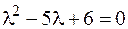 
имеет корни
.
Следовательно, общее решение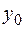 
однородного уравнения имеет вид 
.
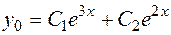Для отыскания частного решения 
анализируем правую часть 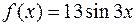, здесь 
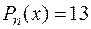, т.е. 
, 
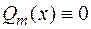, т.е. 
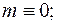тогда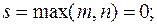 
число 
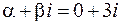не совпадает с корнями характеристического уравнения, следовательно, 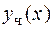выписываем по формуле (8.21): 
.
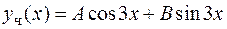Неопределенные коэффициенты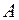 
и 
находятся так:
1) Считаем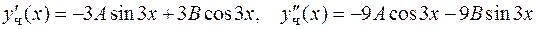 
.
2) Подставляем 
в исходное уравнение:
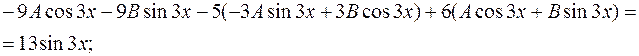или 
.
3) Приравнивая коэффициенты при 
и 
, стоящие в правой и левой частях последнего уравнения, получим систему для определения коэффициентов 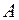и :
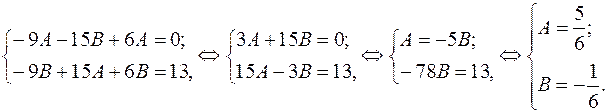
4) Итак, частное решение имеет вид 
, следовательно, общее решение исходного уравнения запишется в форме:
.
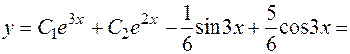
Пример 3. Найти решение задачи Коши
|
|
|
.
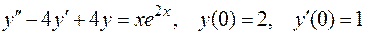Решение. Сначала найдем общее решение этого уравнения. Характеристическое уравнение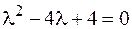 
имеет два равных действительных корня 
. Следовательно, общее решение соответствующего однородного уравнения 
. Частное решение данного уравнения будем искать в виде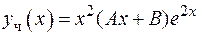 
, так как показатель экспоненты в правой части уравнения 
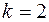совпадает с двукратным корнем характеристического уравнения. Методом неопределенных коэффициентов находим 
, 
. Следовательно,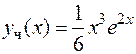 
, а общее решение имеет вид
.
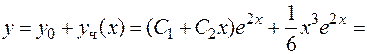
Для определения произвольных постоянных найдем производную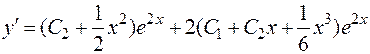 
и используем начальные условия. Получаем: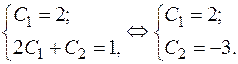 
Следовательно, искомое решение задачи Коши имеет вид 
.
|
|
|
