 |
Интегралы от неограниченных функций
|
|
|
|
(интегралы 2-го рода)
Пусть  непрерывна на
непрерывна на  и имеет бесконечный разрыв в точке b. Если существует конечный предел
и имеет бесконечный разрыв в точке b. Если существует конечный предел  , то он называется несобственным интегралом второго рода и обозначается
, то он называется несобственным интегралом второго рода и обозначается  . Если предел
. Если предел  существует и конечен, то несобственный интеграл
существует и конечен, то несобственный интеграл  сходится. В противном случае несобственный интеграл расходится.
сходится. В противном случае несобственный интеграл расходится.
Пример 1. Вычислить интеграл  .
.
Решение. Так как функция  стремится к бесконечности при
стремится к бесконечности при  , то
, то
 .
.
Таким образом, заданный интеграл расходится.
Пример 2. Вычислить интеграл  .
.
Решение. Подынтегральная функция стремится к бесконечности при  . Следовательно,
. Следовательно,
 .
.
Таким образом, заданный интеграл сходится и равен 2.
Справедливы следующие признаки сходимости.
Теорема. Пусть на  непрерывные функции
непрерывные функции 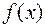 и
и  удовлетворяют условию
удовлетворяют условию  и при
и при  терпят бесконечный разрыв, тогда, если сходится интеграл
терпят бесконечный разрыв, тогда, если сходится интеграл  , то сходится и интеграл
, то сходится и интеграл  и, наоборот, если расходится интеграл
и, наоборот, если расходится интеграл  , то расходится и интеграл
, то расходится и интеграл  .
.
Теорема. Пусть на  непрерывные функции
непрерывные функции 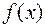 и
и  удовлетворяют условию
удовлетворяют условию  и при
и при  терпят бесконечный разрыв, тогда если
терпят бесконечный разрыв, тогда если  положителен и конечен, то интегралы
положителен и конечен, то интегралы  и
и  сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
Пример 3. Доказать, что  расходится.
расходится.
Решение. Подынтегральная функция 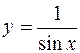 стремится к бесконечности при
стремится к бесконечности при  . Заметим, также, что
. Заметим, также, что  . Рассмотрим интеграл
. Рассмотрим интеграл  . Итак, интеграл
. Итак, интеграл 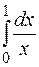 расходится. Следовательно, расходится и интеграл
расходится. Следовательно, расходится и интеграл  .
.
Задачи для самостоятельного решения
1. Вычислить несобственный интеграл  .
.
2. Установить расходимость несобственного интеграла
 .
.
3. Вычислить несобственный интеграл  .
.
4. Установить расходимость несобственного интеграла
 .
.
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Площадь плоской фигуры
 4.1.1. Площадь плоской фигуры, заданной в декартовых координатах
4.1.1. Площадь плоской фигуры, заданной в декартовых координатах
|
|
|
Пусть плоская фигура ограничена линиями  ,
,  ,
,  ,
,  (рис. 1). Тогда ее площадь вычисляется по формуле
(рис. 1). Тогда ее площадь вычисляется по формуле

 Пример 1. Вычислить площадь эллипса:
Пример 1. Вычислить площадь эллипса: 
Решение. Так как эллипс – симметричная фигура, то достаточно найти площадь ее четвертинки (рис. 2). Из уравнения эллипса выразим переменную  :
:  . Тогда площадь эллипса равна
. Тогда площадь эллипса равна



Площадь плоской фигуры, заданной параметрически
Пусть плоская фигура задана параметрически  ,
,  . Тогда ее площадь вычисляется по формуле
. Тогда ее площадь вычисляется по формуле

Пример 2. Вычислить площадь эллипса:  ,
,  ,
,  .
.
Решение. Воспользуемся формулой для вычисления площади фигуры, заданной параметрически. Так как  , то
, то

 .
.
4.1.3. Площадь плоской фигуры, заданной в полярных координатах Пусть фигура задана в полярных координатах  , где угол
, где угол 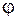 принадлежит отрезку
принадлежит отрезку  . Тогда ее площадь вычисляется по формуле
. Тогда ее площадь вычисляется по формуле  .
.
Пример 3. Вычислить площадь фигуры:  .
.
Решение. Фигура, которая задается формулой  , представляет из себя трилистник (рис. 3).
, представляет из себя трилистник (рис. 3).
 Так как площадь каждого лепестка одинакова,
Так как площадь каждого лепестка одинакова,


 .
.
Задачи для самостоятельного решения
1. Вычислить площадь фигуры, ограниченной линиями:  ,
, 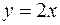 ,
,  .
.
2. Вычислить площадь фигуры, ограниченной линиями:  ,
,  ,
,  ,
,  .
.
3. Вычислить площадь фигуры, заданной параметрически:  ,
,  .
.
4. Вычислить площадь фигуры, заданной параметрически:  ,
,  .
.
5. Вычислить площадьфигуры, заданной в полярных координатах 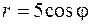 .
.
6. Вычислить площадьфигуры, заданной в полярных координатах  .
.
Длина дуги плоской кривой
4.3.1. Длина дуги плоской кривой, заданной в декартовых координатах  Пусть функция
Пусть функция  и ее производная
и ее производная  заданы и непрерывны на отрезке
заданы и непрерывны на отрезке  . Тогда длина дуги AB (рис. 4) вычисляется по формуле
. Тогда длина дуги AB (рис. 4) вычисляется по формуле

Пример 1. Вычислить длину окружности радиуса R.
Решение. Окружность радиуса  с центром в начале координат задается формулой
с центром в начале координат задается формулой  . Так как окружность симметрична и относительно оси Ox и относительно оси Oy, то достаточно найти длину дуги окружности, расположенной в первой четверти.
. Так как окружность симметрична и относительно оси Ox и относительно оси Oy, то достаточно найти длину дуги окружности, расположенной в первой четверти.
|
|
|
Из равенства  получаем
получаем  ,
,  . Следовательно,
. Следовательно,

 .
.
4.3.2. Длина дуги плоской кривой, заданной параметрически Пусть кривая задана параметрически:  ,
,  ,
,  . Тогда ее длина вычисляется по формуле
. Тогда ее длина вычисляется по формуле
 .
.
Пример 2. Вычислить длину окружности.
Решение. Вычислим длину дуги окружности радиуса  , расположенную в первой четверти и умножим полученный результат на 4. Так как
, расположенную в первой четверти и умножим полученный результат на 4. Так как  ,
,  ,
,  – параметрическое уравнение окружности, а
– параметрическое уравнение окружности, а  ,
,  , то ее длина равна
, то ее длина равна
 .
.
4.3.3. Длина дуги плоской кривой, заданной в полярных координатах Пусть плоская кривая задана в полярных координатах:  ,
,  . Пусть также
. Пусть также  и
и 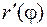 – непрерывные функции на отрезке
– непрерывные функции на отрезке  . Тогда длину кривой можно вычислить по формуле
. Тогда длину кривой можно вычислить по формуле
 .
.
Пример 3. Найти длину кардиоиды  .
.
Решение. Так как  , то
, то

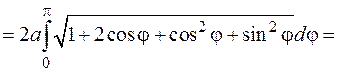

 .
.
|
|
|


