 |
Задачи для самостоятельного решения
|
|
|
|
Задача 1. Найти общее решение уравнений:
а)  б)
б)  в)
в)  .
.
Задача 2. Найти решение задачи Коши:
 .
.
ДОМАШНЕЕ ЗАДАНИЕ
Основные правила и требования
Каждый студент выполняет один вариант задания. Выбор варианта осуществляется по номеру в журнале группы или по указанию преподавателя. Преподаватель также определяет, какие задачи должен решить каждый студент.
Сроки сдачи задания устанавливаются преподавателем.
Варианты задания
Задание 1. Проинтегрировать с помощью замены переменных.
1. 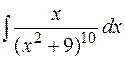 2.
2. 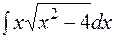 .
3. .
3.  4.
4. 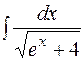 5.
5.  6.
6. 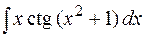 7.
7.  .
8. .
8. 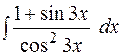 9.
9. 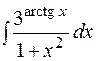 10.
10.  .
11. .
11. 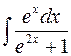 ,
12. ,
12.  23.
23. 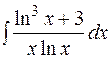 24.
24.  .
25. .
25.  26.
26. 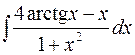
| 13. 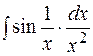 14.
14. 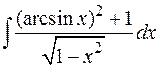 15.
15. 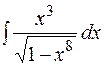 16.
16. 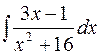 17.
17. 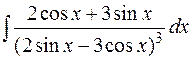 18.
18.  19.
19.  20.
20.  21.
21.  22.
22. 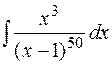 27.
27. 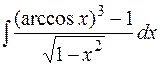 28.
28.  29.
29.  30.
30. 
|
Задание 2. Проинтегрировать по частям.
1. 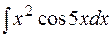 2.
2.  3.
3.  4.
4. 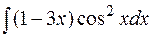 5.
5.  6.
6. 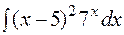 7.
7. 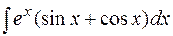 8.
8.  9.
9. 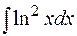 10.
10.  11.
11.  12.
12. 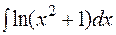 13.
13.  14.
14. 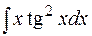 15.
15. 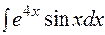
| 16. 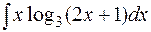 17.
17.  18.
18. 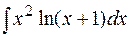 .
19. .
19. 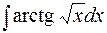 20.
20. 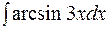 21.
21. 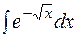 22.
22. 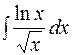 23.
23.  24.
24.  25.
25. 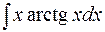 26.
26.  27.
27.  28.
28.  29.
29. 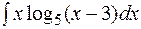 30.
30. 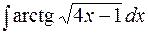
|
Задание 3. Проинтегрировать дробно-рациональные функции.
1. 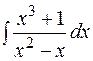 2.
2. 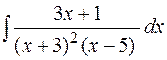 3.
3.  4.
4.  5.
5. 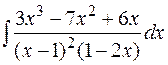 6.
6. 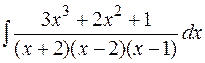 7.
7.  8.
8.  9.
9.  10.
10. 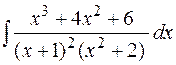 11.
11. 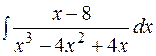 12.
12.  13.
13. 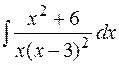 14.
14.  29.
29. 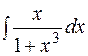
| 15.  16.
16.  17.
17. 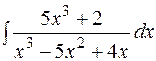 18.
18. 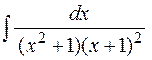 19.
19. 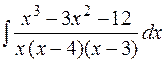 20.
20. 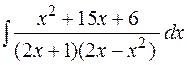 21.
21.  22.
22.  23.
23. 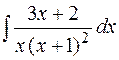 24.
24.  25.
25.  26.
26.  27.
27. 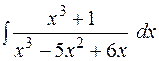 28.
28.  30
30 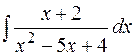 . .
|
Задание 4. Найти интегралы от тригонометрических функций.
1. 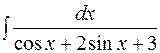 2.
2.  3.
3. 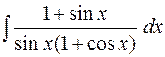 4.
4.  5.
5. 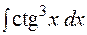 6.
6.  7.
7.  8.
8. 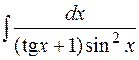 9.
9. 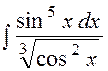 10.
10.  11.
11.  12.
12. 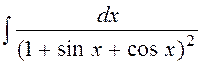 13.
13.  14.
14.  15.
15. 
| 16. 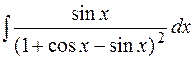 17.
17.  18.
18. 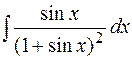 19.
19.  20.
20.  21.
21.  22.
22. 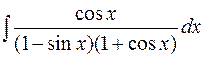 23.
23. 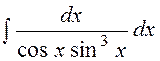 24.
24. 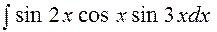 25.
25.  26.
26. 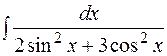 27.
27.  28.
28.  29.
29.  30.
30. 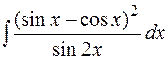
|
Задание 5. Найти интегралы от иррациональных функций.
1. 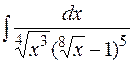 2.
2.  3.
3.  4.
4. 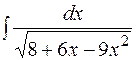 5.
5.  6.
6. 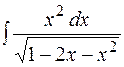 7.
7.  8.
8. 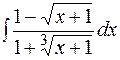 9.
9.  10.
10. 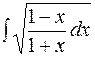 11.
11.  12.
12. 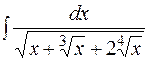 13.
13. 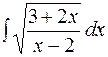 14.
14.  15.
15. 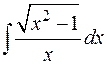
| 16. 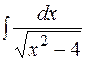 17.
17.  18.
18.  19.
19. 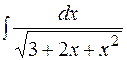 20.
20.  21.
21.  22.
22.  23.
23. 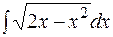 24.
24. 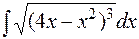 25.
25.  26.
26. 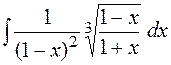 27.
27. 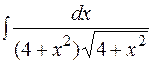 28.
28.  29.
29. 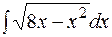 30.
30. 
|
Задание 6. Вычислить определенный интеграл.
| 1. | а) 
| б) 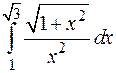
|
| 2. | а) 
| б) 
|
| 3. | а) 
| б) 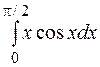
|
| 4. | а) 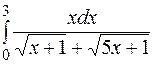
| б) 
|
| 5. | а) 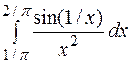
| б) 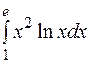
|
| 6. | а) 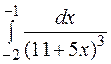
| б) 
|
| 7. | а) 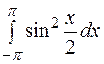
| б) 
|
| 8. | а) 
| б) 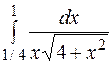
|
| 9. | а) 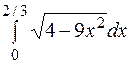
| б) 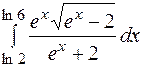
|
| 10. | а) 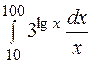
| б) 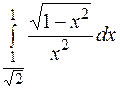
|
| 11. | а) 
| б) 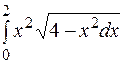
|
| 12. | а) 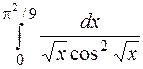
| б) 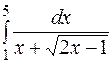
|
| 13. | а) 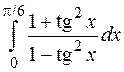
| б) 
|
| 14. | а) 
| б) 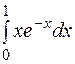
|
| 15. | а) 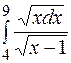
| б) 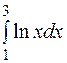
|
| 16. | а) 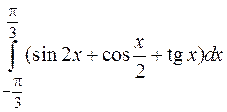
| б) 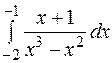
|
| 17. | а) 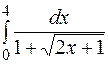
| б) 
|
| 18. | а) 
| б)  ` `
|
| 19. | а) 
| б) 
|
| 20. | а) 
| б) 
|
| 21. | а) 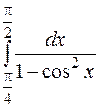
| б) 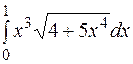
|
| 22. | а) 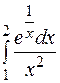
| б) 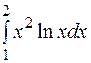
|
| 23. | а) 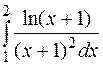
| б) 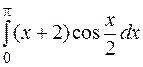
|
| 24. | а) 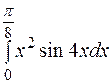
| б) 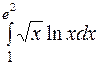
|
| 25. | а) 
| б) 
|
| 26. | а) 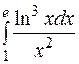
|
б) 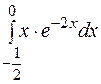
|
| 27. | а) 
| б) 
|
| 28. | а) 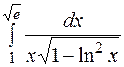
| б) 
|
| 29. | а) 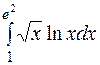
| б) 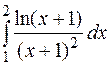
|
| 30. | а) 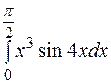
| б) 
|
|
|
|
Задание 7. Вычислить несобственный интеграл или установить
его расходимость.
1. 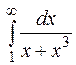
| 10. 
|
2. 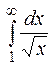
| 11. 
|
3. 
| 12. 
|
4. 
| 13. 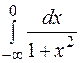
|
5. 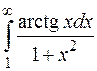
| 14. 
|
6. 
| 15. 
|
7. 
| 16. 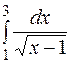
|
8. 
| 17. 
|
9. 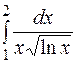
| 18. 
|
19. 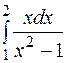
| 25. 
|
20. 
| 26. 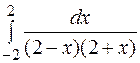
|
21. 
| 27. 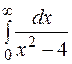
|
22. 
| 28. 
|
23. 
| 29. 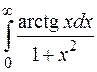
|
24. 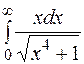
| 30. 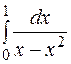
|
Задание 8. Вычислите площадь фигуры, ограниченной заданными линиями.
1.  ,
, 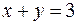
2.  ,
, 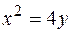
3. 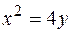 ,
, 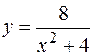
4.  ,
,  ,
, 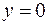
5. 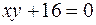 ,
,  ,
, 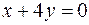
6.  ,
, 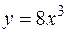 ,
, 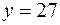
7.  ,
, 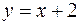
8. 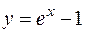 ,
,  ,
, 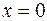
9. 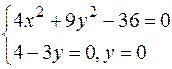
10.  ,
,  ,
, 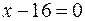
11. 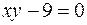 ,
, 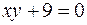 ,
, 
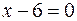
12.  ,
, 
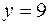
13.  ,
, 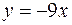
14.  ,
,  ,
, 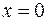 ,
, 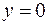
15. 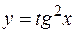 ,
, 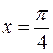 ,
, 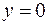
16.  ,
, 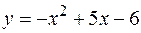
17. 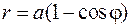
18. 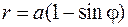
19. 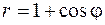
20. 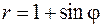
21. 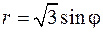
22. 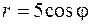
23. 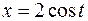 ,
,  ,
, 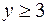
24. 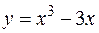 ,
, 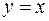
25. 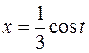 ,
, 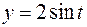
26. 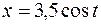 ,
, 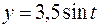
27.  ,
, 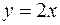 ,
, 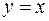
28.  ,
, 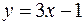
29.  ,
, 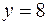 ,
, 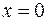
30. 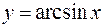 ,
, 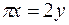
Задание 9. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
1.  ,
,  вокруг оси
вокруг оси 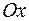
2. 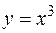 ,
, 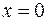 ,
, 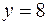 вокруг оси
вокруг оси 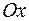
3. 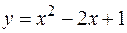 ,
, 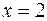 ,
, 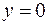 , вокруг оси
, вокруг оси 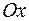
4.  ,
, 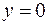 , вокруг оси
, вокруг оси 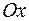
5. 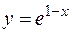 ,
, 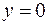 ,
, 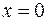 ,
,  вокруг оси
вокруг оси 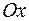
6. 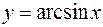 ,
, 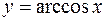 ,
, 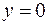 вокруг оси
вокруг оси 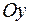 .
.
7. 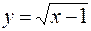 ,
, 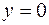 ,
,  ,
, 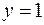 вокруг оси
вокруг оси 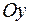 .
.
8.  ,
,  ,
, 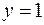 вокруг оси
вокруг оси 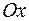 .
.
9.  ,
,  вокруг оси
вокруг оси 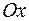 .
.
10. 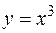 ,
, 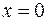 ,
, 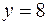 вокруг оси
вокруг оси 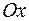 .
.
11. 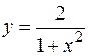 ,
, 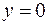 ,
, 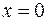 ,
,  вокруг оси
вокруг оси 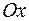 .
.
12. 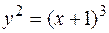 ,
, 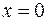 вокруг оси
вокруг оси 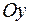 .
.
13. 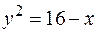 ,
, 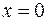 вокруг оси
вокруг оси 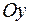 .
.
14.  ,
, 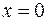 ,
, 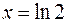 вокруг оси
вокруг оси 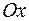 .
.
15.  ,
, 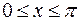 вокруг оси
вокруг оси 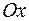 .
.
16.  ,
,  вокруг оси
вокруг оси 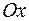 .
.
17.  ,
, 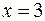 ,
,  вокруг оси
вокруг оси 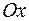 .
.
18. 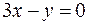 ,
, 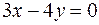 ,
,  вокруг оси
вокруг оси 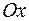 .
.
19.  ,
,  ,
, 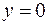 вокруг оси
вокруг оси 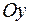 .
.
20.  ,
, 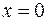 ,
, 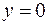 вокруг оси
вокруг оси 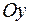 .
.
21. 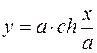 ,
,  ,
,  вокруг оси
вокруг оси 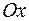 .
.
22. 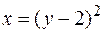 ,
, 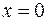 ,
, 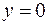 вокруг оси
вокруг оси 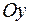 .
.
23. 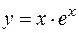 ,
,  ,
, 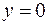 вокруг оси
вокруг оси 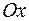 .
.
24. 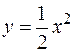 ,
,  вокруг оси
вокруг оси 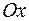 .
.
25.  ,
, 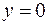 вокруг оси
вокруг оси 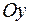 .
.
26.  ,
, 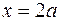 вокруг оси
вокруг оси 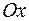 .
.
27.  ,
,  ,
, 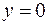 вокруг оси
вокруг оси 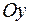 .
.
28.  ,
,  вокруг оси
вокруг оси 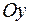 .
.
29.  вокруг оси
вокруг оси 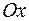 .
.
30.  вокруг оси
вокруг оси 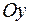 .
.
Задание 10. Найдите длину дуги кривой
1. 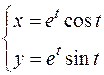 ,
, 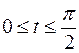
2. 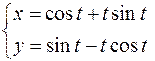 ,
, 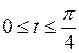
3. 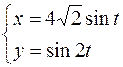 ,
, 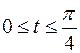
4. 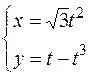 ,
, 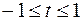
5.  ,
, 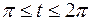
6. 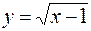 от точки A (1;0) до точки B (2;1).
от точки A (1;0) до точки B (2;1).
7.  от
от 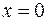 до
до  .
.
8.  от вершины до точки с абсциссой
от вершины до точки с абсциссой 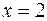 .
.
9.  от
от  до
до 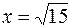 .
.
10. 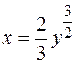 от точки О(0;0) до точки А (
от точки О(0;0) до точки А ( ;3).
;3).
11. 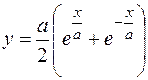 между точками, абсциссы которых равны 0 и a.
между точками, абсциссы которых равны 0 и a.
12.  между точками пересечения с осью
между точками пересечения с осью 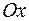 .
.
13. 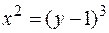 , отсеченной прямой
, отсеченной прямой  .
.
14.  .
.
15.  .
.
16. 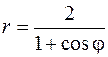 .
.
17.  .
.
18. 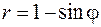 ,
, 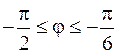 .
.
19. 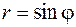 ,
, 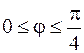 .
.
20. 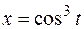 ,
,  ,
, 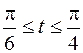 .
.
21.  ,
, 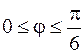 .
.
22. 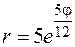 ,
, 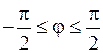 .
.
23. 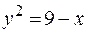 ,
, 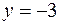 ,
, 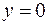 .
.
24.  , отсеченной прямой
, отсеченной прямой 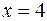 .
.
25. 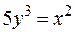 , заключенной внутри окружности
, заключенной внутри окружности 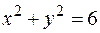 .
.
26.  ,
, 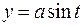 .
.
27.  .
.
28. 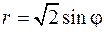 .
.
29.  от
от  до
до  .
.
30.  .
.
Задание 11.
1. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями  ,
, 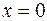 .
.
2. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями 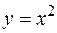 ,
,  .
.
3. Вычислить двойной интеграл 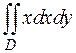 по области D, ограниченной линиями
по области D, ограниченной линиями  ,
,  ,
, 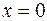 .
.
4. Вычислить двойной интеграл 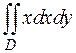 по области D, ограниченной линиями
по области D, ограниченной линиями  ,
,  .
.
|
|
|
5. Вычислить двойной интеграл 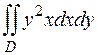 по области D, ограниченной линиями
по области D, ограниченной линиями 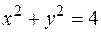 ,
,  .
.
6. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями 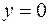 ,
,  (
(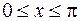 ).
).
7. Вычислить двойной интеграл 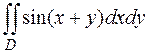 по области D, ограниченной линиями
по области D, ограниченной линиями  ,
,  ,
, 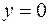 .
.
8. Вычислить двойной интеграл  по области D, ограниченной кривой
по области D, ограниченной кривой 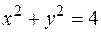 .
.
9. Вычислить двойной интеграл 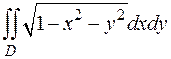 по области D, ограниченной кривой
по области D, ограниченной кривой  .
.
10. Вычислить двойной интеграл 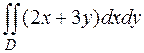 по области D, ограниченной линиями
по области D, ограниченной линиями 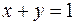 ,
, 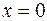 ,
, 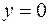 .
.
11. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями 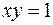 ,
,  .
.
12. Вычислить двойной интеграл 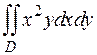 по области D, ограниченной линиями
по области D, ограниченной линиями 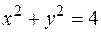 ,
, 
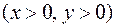 .
.
13. Вычислить двойной интеграл  по области D, ограниченной кривой
по области D, ограниченной кривой  .
.
14. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями 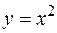 ,
, 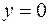 ,
,  .
.
15. Вычислить двойной интеграл 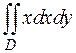 по области D, ограниченной линиями
по области D, ограниченной линиями  ,
, 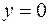 ,
, 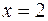 .
.
16. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями 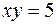 ,
, 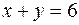 .
.
17. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями 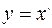 ,
, 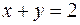 ,
,  .
.
18. Вычислить двойной интеграл  по области D, ограниченной окружностью
по области D, ограниченной окружностью 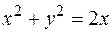 .
.
19. Вычислить двойной интеграл 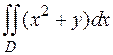 по области D, ограниченной параболами
по области D, ограниченной параболами 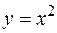 и
и  .
.
20. Вычислить двойной интеграл 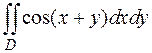 по области D, ограниченной прямыми
по области D, ограниченной прямыми  ,
,  ,
, 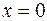 .
.
21. Вычислить двойной интеграл  по области D, ограниченной кривой
по области D, ограниченной кривой 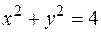 .
.
22. Вычислить двойной интеграл  по области D, ограниченной кривой
по области D, ограниченной кривой  .
.
23. Вычислить двойной интеграл 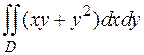 по области D, ограниченной линиями
по области D, ограниченной линиями 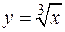 ,
, 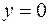 ,
,  .
.
24. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями  ,
, 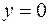 ,
,  .
.
25. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями 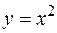 ,
,  .
.
26. Вычислить двойной интеграл  по области D, ограниченной кривой
по области D, ограниченной кривой 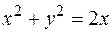 .
.
27. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями  ,
, 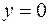 ,
,  .
.
28. Вычислить двойной интеграл 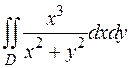 по области D, ограниченной кривой
по области D, ограниченной кривой  .
.
29. Вычислить двойной интеграл 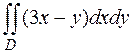 по области D, ограниченной линиями
по области D, ограниченной линиями 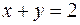 ,
, 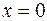 ,
, 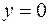 .
.
30. Вычислить двойной интеграл  по области D, ограниченной линиями
по области D, ограниченной линиями  ,
, 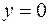 ,
,  .
.
Задание 12.
1. Вычислить объем тела, ограниченного поверхностями
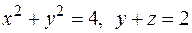 и
и  .
.
2. Вычислить объем тела, ограниченного поверхностями


