 |
Интегрирование рациональных дробей
|
|
|
|
Рациональные дроби вида
1) 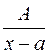 2)
2) 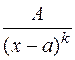 3)
3) 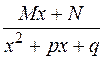 4)
4) 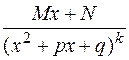 ,
,
где 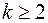 и дискриминант многочлена
и дискриминант многочлена 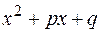 отрицателен, называются простейшими рациональными дробями 1, 2, 3 и 4 типов.
отрицателен, называются простейшими рациональными дробями 1, 2, 3 и 4 типов.
Найдем интегралы от простейших рациональных дробей 1–3 типов.
1) 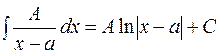 (по таблице интегралов).
(по таблице интегралов).
2) 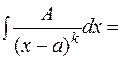 (замена
(замена 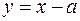 ,
, 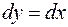 ) =
) =  =
=
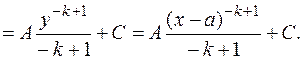
3) 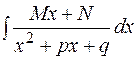 = (выделим в знаменателе полный квадрат)
= (выделим в знаменателе полный квадрат)
= 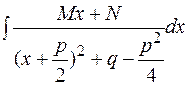 .
.
Заметим, что 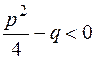 (дискриминант). Положим
(дискриминант). Положим
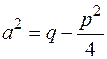 и сделаем подстановку
и сделаем подстановку 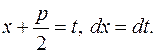 Интеграл примет вид:
Интеграл примет вид:
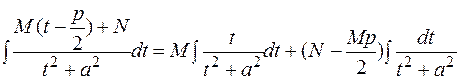 =
=
= 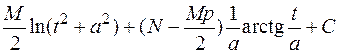 .
.
Возвращаясь к переменной 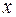 , получаем ответ:
, получаем ответ:
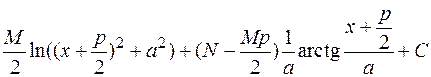 .
.
Известно, что произвольный многочлен 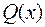 может разлагаться на множители двух видов:
может разлагаться на множители двух видов: 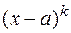 ,
, 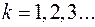 или
или 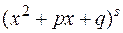 ,
, 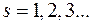 , причем квадратный трехчлен
, причем квадратный трехчлен 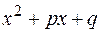 имеет отрицательный дискриминант (не разлагается на множители). Строго эта теорема звучит так:
имеет отрицательный дискриминант (не разлагается на множители). Строго эта теорема звучит так:
Теорема. Всякий многочлен 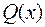 степени
степени 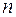 с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами
с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами
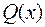 =
= 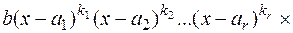
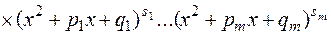 .
.
При этом 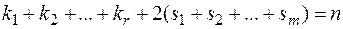 .
.
Выражение 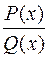 называется правильной дробно-рациональной функцией, если
называется правильной дробно-рациональной функцией, если 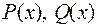 – многочлены, причем степень знаменателя больше степени числителя.
– многочлены, причем степень знаменателя больше степени числителя.
Интегрирование дробно-рациональных функций основано на следующей теореме о разложении:
Теорема. Всякую правильную рациональную дробь 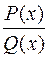 , знаменатель которой разложен на множители
, знаменатель которой разложен на множители
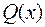 =
= 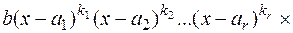
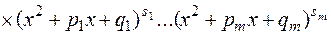
можно представить единственным образом в виде следующей суммы простейших дробей:
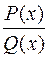 =
= 
+ 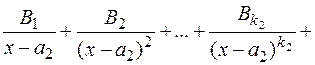 ...
...
...+ 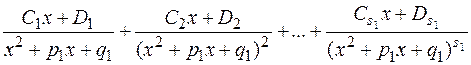 +...
+...
...+ 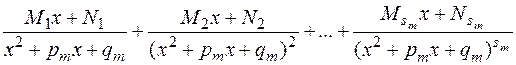 ,
,
где 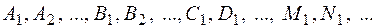 – некоторые действительные коэффициенты.
– некоторые действительные коэффициенты.
Пример 1. Дробь 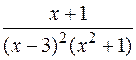 представима в виде
представима в виде
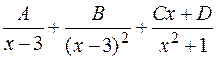 .
.
Пример 2. Представим дробь 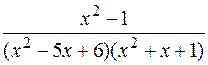 в виде суммы простейших дробей.
в виде суммы простейших дробей.
Решение. Заметим, что выражение (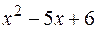 ) разлагается на множители
) разлагается на множители 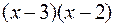 . Потому
. Потому
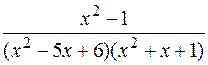 =
= 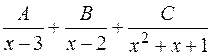 .
.
Отметим также, что числитель не влияет на вид разложения, а будет влиять только на значения коэффициентов 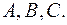
Таким образом, можно свести вычисление дробно-рациональной функции к вычислению простейших дробей. Для этого необходимо вычислить неопределенные коэффициенты, возникающие при разложении. Они вычисляются методом неопределенных коэффициентов. Продемонстрируем его на следущем примере.
|
|
|
Пример. Пусть имеется разложение
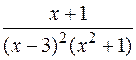 =
= 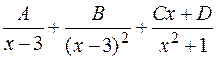 .
.
Найти все коэффициенты этого разложения.
Решение.
Приводим правую часть равенства к общему знаменателю:
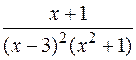 =
= 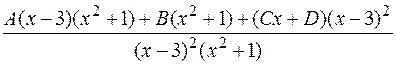 =
=
= 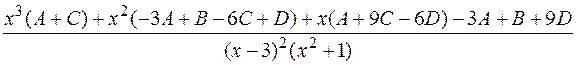
Затем сравниваем коэффициенты при одинаковых степенях 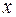 в числителях левой и правой частей. Получаем систему:
в числителях левой и правой частей. Получаем систему:
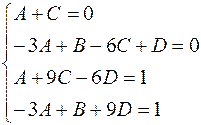
Решая ее, получаем искомые коэффициенты:
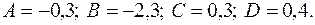
Заметим, что неправильную дробно-рациональную функцию 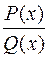 можно превратить в сумму многочлена и правильной дроби с помощью деления углом, т.е.
можно превратить в сумму многочлена и правильной дроби с помощью деления углом, т.е.
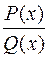 =
= 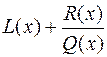 ,
,
где 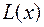 – многочлен,
– многочлен, 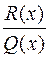 – правильная дробь.
– правильная дробь.
Пример. Дана неправильная рациональная дробь
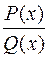 =
= 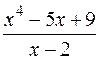 .
.
Разделим числитель на знаменатель:
_  |
| 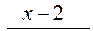
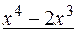
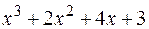
_ 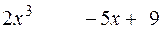
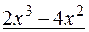
_ 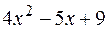
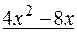
_ 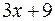
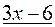
Результат деления:
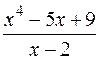 =
= 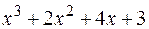 +
+ 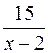 .
.
Сформулируем теперь общее правило интегрирования рациональных дробей.
1. Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби.
2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
3. Проинтегрировать многочлен и полученную сумму простейших дробей.
Пример 1. Вычислить 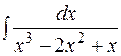 .
.
Решение. Представим подынтегральное выражение в виде
суммы простейших дробей:
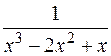 =
= 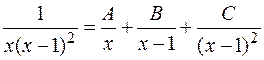 .
.
Методом неопределенных коэффициентов находим неизвестные
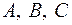 :
:
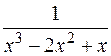 =
= 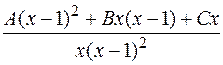 =
=
= 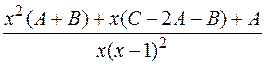
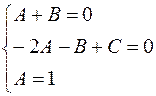
Отсюда 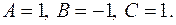 Тогда
Тогда
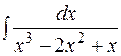 =
= 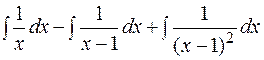 =
=
= 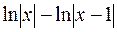
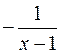 + C.
+ C.
Пример 2. Вычислить 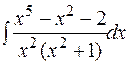 .
.
Решение. Дробь неправильная, поэтому делим многочлены углом и выделяем многочлен и правильную дробь
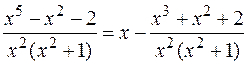
Далее, разложим получившуюся правильную дробь на простейшие дроби
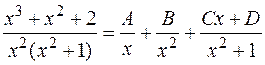 =
= 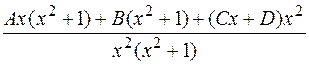
Методом неопределенных коэффициентов находим коэффициенты:
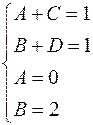
Следовательно, 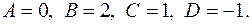
Таким образом,
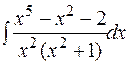 =
= 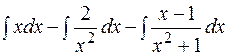 =
= 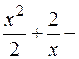
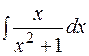 +
+
+ 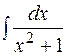 =
= 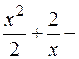
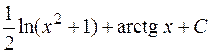 .
.
Задачи для самостоятельного решения
а) 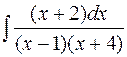 б)
б) 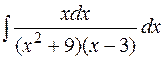 в)
в) 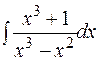
г) 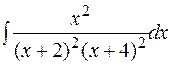 д)
д) 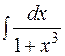 е)
е) 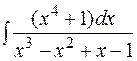
|
|
|


