 |
Интегрирование тригонометрических функций
|
|
|
|
1. Рассмотрим интегралы вида  .
.
Если хотя бы одно из чисел  – нечетное положительное, то делаем замену: функцию в четной степени обозначаем новой переменной. От функции в нечетной степени отделяем один множитель, оставшуюся четную степень выражаем через дополнительную функцию с помощью формул
– нечетное положительное, то делаем замену: функцию в четной степени обозначаем новой переменной. От функции в нечетной степени отделяем один множитель, оставшуюся четную степень выражаем через дополнительную функцию с помощью формул  и
и  .
.
Пример. Найти  .
.
Решение.
 =
= 
 =
=
=  =
=  =
=  =
=  =
=
=  .
.
Если оба числа  – четные неотрицательные, то применяем формулы понижения степени
– четные неотрицательные, то применяем формулы понижения степени
 ,
,  ,
,  .
.
Пример. Найти  .
.
Решение.
 =
=  =
=  =
=  =
=
= 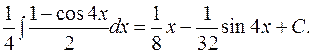
2. Интегралы вида  и
и  вычисляются соответственно с помощью подстановок:
вычисляются соответственно с помощью подстановок:  .
.
Пример. Найти  .
.
Решение.
 =
=  =
=  =
=  =
=  =
=
=  =
= 
 .
.
3. При вычислении интегралов
 ,
,  ,
, 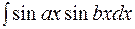
применяют формулы
 ,
,
 ,
,

 .
.
Пример. Найти  .
.
Решение.
 =
=  =
=  =
=
=  .
.
4. Пусть  – рациональная функция своих аргументов
– рациональная функция своих аргументов  , т.е. над
, т.е. над  и
и  совершаются только арифметические операции. Например,
совершаются только арифметические операции. Например,  =
=  – рациональная функция, а
– рациональная функция, а  =
=  – не является рациональной.
– не является рациональной.
Интегралы вида  , где
, где  – рациональная функция аргументов
– рациональная функция аргументов  приводятся к интегралам от рациональной функции нового аргумента
приводятся к интегралам от рациональной функции нового аргумента  с помощью универсальной подстановки
с помощью универсальной подстановки  . При этом
. При этом
 ,
,  ,
,  .
.
Пример. Найти  .
.
Решение. Делая подстановку
 ,
,  ,
,  ,
,  ,
,
получим
 =
=  =
= 
 =
=
=  .
.
Задачи для самостоятельного решения
а)  б)
б)  в)
в) 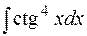
г)  д)
д)  е)
е) 
Интегрирование дробно-линейных иррациональностей
Пусть  – рациональная функция. Функцию вида
– рациональная функция. Функцию вида  называют дробно-линейной иррациональностью.
называют дробно-линейной иррациональностью.
Замена  рационализирует интеграл
рационализирует интеграл  . Это следует из того, что
. Это следует из того, что  (а, значит, и
(а, значит, и  ) – рациональная функция.
) – рациональная функция.
Пример 1. Вычислить  .
.
Решение. Полагая  , получим
, получим  ,
,  ,
,  . Таким образом,
. Таким образом,
 =
=  =
=  =
=  =
=
=  + C.
+ C.
Пример 2. Вычислить  .
.
Решение.  =
=  =
=  =
=  =
=
= 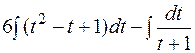 =
=  + C =
+ C =
 .
.
Задачи для самостоятельного решения
а)  б)
б)  в)
в) 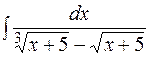
г)  д)
д)  е)
е) 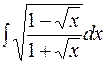
Интегрирование квадратичных иррациональностей
|
|
|
Пусть  – рациональная функция. Функцию
– рациональная функция. Функцию  будем называть квадратичной иррациональностью. Пусть нужно вычислить интеграл
будем называть квадратичной иррациональностью. Пусть нужно вычислить интеграл
 .
.
Выделив под знаком корня полный квадрат  =
=  и сделав подстановку
и сделав подстановку  , получим интеграл одного из следующих типов:
, получим интеграл одного из следующих типов:
1.  .
.
2. 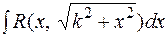
3. 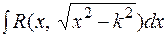
В каждом из них можно избавиться от иррациональности с помощью следующих тригонометрических подстановок:
1. 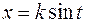
2. 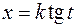
3. 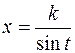
Пример 1.
 =
=  =
= 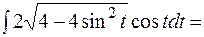
=  =
=  =
=  =
= 
 .
.
Пример 2.
 =
=  =
=
= 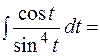
 =
=  =
=  =
=  .
.
Пример 3.
 =
= 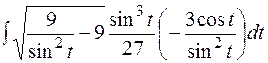 =
=
=  (см. предыдущий пример) =
(см. предыдущий пример) =
= 


 .
.
Задачи для самостоятельного решения
а)  б)
б)  в)
в) 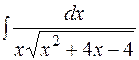
г)  д)
д)  е)
е) 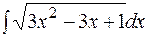
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенный интеграл и его свойства
Пусть на отрезке [ a; b ],  , задана функция
, задана функция  . Разобьем данный отрезок на
. Разобьем данный отрезок на 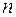 частичных отрезков
частичных отрезков  , где
, где  . В каждом из отрезков
. В каждом из отрезков  возьмем произвольную точку
возьмем произвольную точку  и составим сумму
и составим сумму
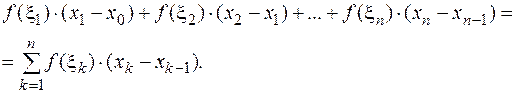
Данную сумму обозначим через  и назовем интегральной суммой функции
и назовем интегральной суммой функции  .
.
Если интегральная сумма имеет предел, который не зависит ни от разбиения отрезка [ a; b ], ни от выбора точек  , то этот предел называется определенным интегралом от функции
, то этот предел называется определенным интегралом от функции  на отрезке [ a; b ], т.е.
на отрезке [ a; b ], т.е.
 ,
,
где 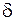 – наибольшая из длин отрезков
– наибольшая из длин отрезков  ,
,  .
.
Функция  , для которой существует определенный интеграл на отрезке [ a; b ], называется интегрируемой на этом отрезке.
, для которой существует определенный интеграл на отрезке [ a; b ], называется интегрируемой на этом отрезке.
Перечислим ряд свойств определенного интеграла.
1. Если 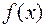 интегрируема на [ a; b ] функция, то
интегрируема на [ a; b ] функция, то  также интегрируемая на [ a; b ] функция и
также интегрируемая на [ a; b ] функция и  .
.
2. Если 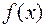 и
и  интегрируемые на [ a; b ] функции, то их сумма, также интегрируемая на [ a; b ] функция и
интегрируемые на [ a; b ] функции, то их сумма, также интегрируемая на [ a; b ] функция и  .
.
3.  =0.
=0.
4.  .
.
5. Пусть функция 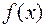 интегрируема в наибольшем из промежутков
интегрируема в наибольшем из промежутков  ,
,  ,
,  . Тогда она интегрируема в двух других промежутках и имеет место равенство
. Тогда она интегрируема в двух других промежутках и имеет место равенство 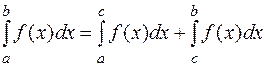 .
.
6. Пусть функция 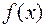 интегрируема на [ a; b ],
интегрируема на [ a; b ],  и
и 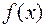 неотрицательна на [ a; b ]. Тогда она интегрируема и имеет место равенство
неотрицательна на [ a; b ]. Тогда она интегрируема и имеет место равенство 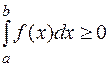 .
.
7. Пусть 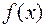 и
и  интегрируемы на [ a; b ] и
интегрируемы на [ a; b ] и  на
на  . Тогда
. Тогда  .
.
8. Пусть функция 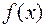 интегрируема на
интегрируема на  ,
,  . Тогда
. Тогда  также интегрируема на
также интегрируема на  и
и  .
.
9. Пусть функция 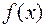 интегрируема на
интегрируема на  и для произвольного
и для произвольного  выполняется соотношение
выполняется соотношение  . Тогда
. Тогда  .
.
|
|
|
10. Пусть функция 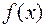 непрерывна на
непрерывна на  , тогда найдется такая точка
, тогда найдется такая точка  , что
, что  .
.
Вычисление интеграла
|
|
|


