 |
Задачи для самостоятельного решения
|
|
|
|
Задача 1.Изменить порядок интегрирования в двойном интеграле 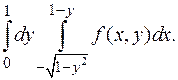
Задача 2. Вычислить двойной интеграл  по области
по области 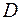 , ограниченной кривыми
, ограниченной кривыми  и
и  .
.
Задача 3. Найти объем тела  ограниченного поверхностями
ограниченного поверхностями 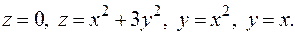
Замена переменных в двойном интеграле
Пусть в двойном интеграле 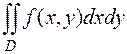 прямоугольные координаты
прямоугольные координаты 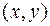 преобразуются к новым координатам
преобразуются к новым координатам  которые связаны с
которые связаны с 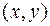 соотношениями:
соотношениями:
 (5.10)
(5.10)
Если между областями 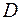 и
и 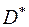 , лежащими в плоскостях
, лежащими в плоскостях  и
и 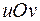 (рис. 11), установлено соотношениями (5.10) взаимно однозначное отображение, причем функции (5.10) имеют непрерывные частные производные первого порядка в области
(рис. 11), установлено соотношениями (5.10) взаимно однозначное отображение, причем функции (5.10) имеют непрерывные частные производные первого порядка в области 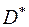 и якобиан отображения в области
и якобиан отображения в области 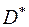 не обращается в нуль, т.е.
не обращается в нуль, т.е.
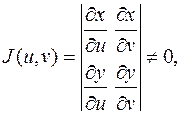
то имеет место следующая формула замены переменных в двойном интеграле
 (5.11)
(5.11)
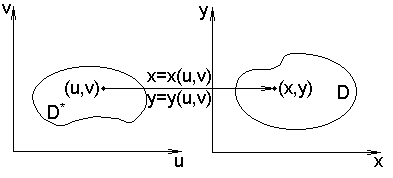
Рис. 11. Отображение областей
В полярных координатах формулы (5.10) имеют вид 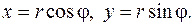 Эти формулы связывают прямоугольные координаты
Эти формулы связывают прямоугольные координаты 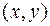 с полярными координатами
с полярными координатами 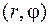 при условии, что полюс помещен в начало координат и полярная ось направлена вдоль оси
при условии, что полюс помещен в начало координат и полярная ось направлена вдоль оси 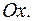 В этом случае
В этом случае 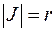 и формула (5.11) принимает вид
и формула (5.11) принимает вид


Для области 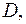 ограниченной лучами, образующими с полярной осью углы
ограниченной лучами, образующими с полярной осью углы 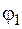 и
и 
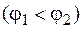 , и кривыми
, и кривыми 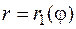 и
и 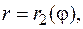 причем
причем 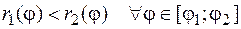 (см. рис. 12), получаем
(см. рис. 12), получаем
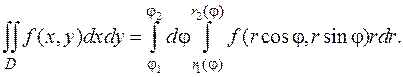 (5.12)
(5.12)
Если область 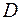 содержит начало координат (см. рис. 13), то
содержит начало координат (см. рис. 13), то
 (5.13)
(5.13)
| 
|
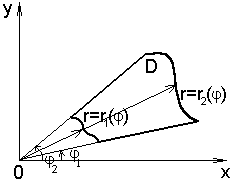
Рис. 12. Область D Рис. 13. Область D содержит
начало координат
Формулы (5.12) и (5.13) удобно использовать при решении задач, когда область 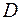 есть круг или часть круга.
есть круг или часть круга.
Обобщенными полярными координатами называют переменные 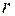 и
и 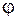 , связанные с прямоугольными координатами
, связанные с прямоугольными координатами 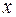 и
и  формулами
формулами  где
где 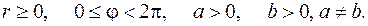
В этом случае 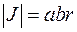 и формула (5.11) принимает вид
и формула (5.11) принимает вид
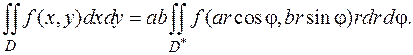
Примеры.
Задача 1. Найти объем тела 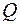 , ограниченного поверхностями
, ограниченного поверхностями 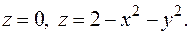
Решение. Данное тело можно представить в виде  где
где 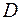 – область на плоскости
– область на плоскости 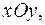 ограниченная окружностью
ограниченная окружностью 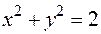 , т.е.
, т.е.  Поэтому
Поэтому  . Перейдем в этом интеграле к полярным координатам:
. Перейдем в этом интеграле к полярным координатам: 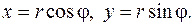
|
|
|
В этих координатах область интегрирования записывается так: 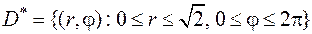 . Следовательно, используя формулу (5.13), получим
. Следовательно, используя формулу (5.13), получим
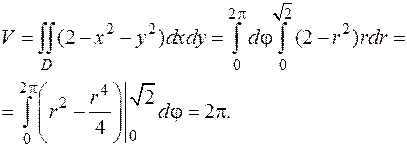
Задача 2. Найти моменты инерции относительно осей координат пластины с плотностью  ограниченной кривыми
ограниченной кривыми 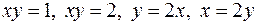 и расположенной в I квадранте.
и расположенной в I квадранте.
Решение. Данная пластина  изображена на рис. 14.
изображена на рис. 14.
 Рис. 14. Область D
Рис. 14. Область D
| По формулам (5.7) имеем 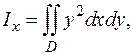 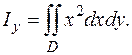 Для вычисления этих интегралов удобнее перейти к полярным координатам:
Для вычисления этих интегралов удобнее перейти к полярным координатам: 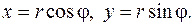
|
Тогда 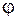 изменяется от
изменяется от 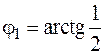 до
до 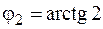 (см. рис. 14), а при каждом значении
(см. рис. 14), а при каждом значении 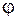 из отрезка
из отрезка 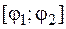 переменная
переменная 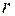 изменяется от
изменяется от 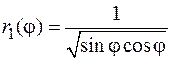 (значение
(значение 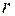 на кривой
на кривой 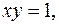 уравнение которой в полярных координатах в I квадранте имеет вид
уравнение которой в полярных координатах в I квадранте имеет вид 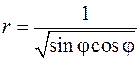 ) до
) до 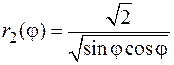 (значение
(значение 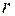 на кривой
на кривой 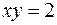 ). Следовательно, используя формулу (5.12), получим
). Следовательно, используя формулу (5.12), получим
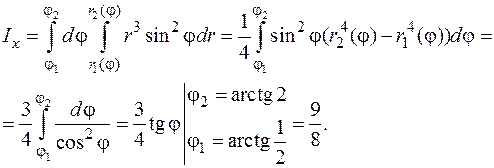
Аналогично получаем 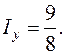
Задачи для самостоятельного решения
Задача 1. Вычислить интеграл 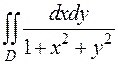 по области
по области 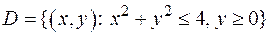 в полярных координатах.
в полярных координатах.
Задача 2. Найти площадь области 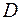 , ограниченной кривыми
, ограниченной кривыми 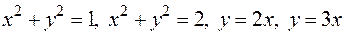 .
.
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПЕРВОГО РОДА
Криволинейные интегралы первого рода
И их приложения
Пусть на плоскости  расположена ограниченная кривая
расположена ограниченная кривая  , гладкая или кусочно-гладкая, функция
, гладкая или кусочно-гладкая, функция 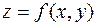 определена и ограничена на кривой
определена и ограничена на кривой  . Разобьем кривую
. Разобьем кривую  на
на 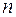 частей
частей 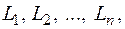 не имеющих общих внутренних точек и на каждой из этих частичных дуг кривой возьмем произвольную точку
не имеющих общих внутренних точек и на каждой из этих частичных дуг кривой возьмем произвольную точку  и составим интегральную сумму
и составим интегральную сумму
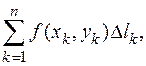 (6.1)
(6.1)
где 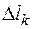 – длина
– длина 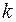 -той частичной дуги
-той частичной дуги 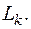
Пусть 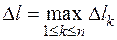 . Если существует предел интегральной суммы (6.1) при
. Если существует предел интегральной суммы (6.1) при  не зависящей от способа дробления кривой
не зависящей от способа дробления кривой  на части
на части  и от выбора промежуточных точек
и от выбора промежуточных точек  то этот предел называется криволинейным интегралом 1-го рода от функции
то этот предел называется криволинейным интегралом 1-го рода от функции  по кривой
по кривой  и обозначается
и обозначается
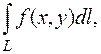
т.е. 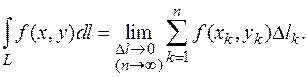 (6.2)
(6.2)
Из определения криволинейного интеграла следует, что его величина не зависит от того, в каком направлении обходят кривую 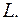
Кривая  может быть замкнутой, в этом случае для обозначения криволинейного интеграла употребляют символ
может быть замкнутой, в этом случае для обозначения криволинейного интеграла употребляют символ 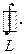
|
|
|
Если 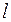 – длина кривой
– длина кривой  , то из формулы (6.2) при
, то из формулы (6.2) при  следует, что
следует, что 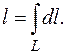
Если кривая  – материальная, т.е. вдоль кривой распределена с плотностью
– материальная, т.е. вдоль кривой распределена с плотностью  некоторая масса
некоторая масса 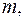 то
то 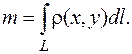
Если кривая  задана параметрически:
задана параметрически: 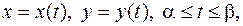 то
то
 (6.3)
(6.3)
если кривая  задана уравнением
задана уравнением 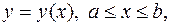 то
то
 (6.4)
(6.4)
если кривая  задана уравнением в полярных координатах
задана уравнением в полярных координатах 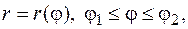 то
то
 (6.5)
(6.5)
Понятие криволинейного интеграла 1-го рода распространяется и на случай функции трех переменных 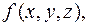 заданной в точках пространственной кривой. Вычисление такого интеграла по кривой
заданной в точках пространственной кривой. Вычисление такого интеграла по кривой  , заданной параметрически
, заданной параметрически 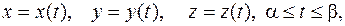 производится по формуле
производится по формуле
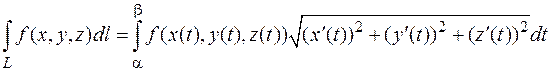 (6.6)
(6.6)
Примеры.
Задача 1. Вычислить 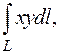 где
где  часть эллипса
часть эллипса 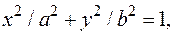 лежащая в I квадранте.
лежащая в I квадранте.
Решение. Параметрическое задание эллипса имеет вид 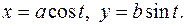 Поскольку рассматривается часть эллипса, лежащая в I квадранте, то
Поскольку рассматривается часть эллипса, лежащая в I квадранте, то  Поэтому, так как
Поэтому, так как  то применяя формулу (6.3) получим
то применяя формулу (6.3) получим
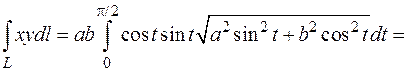
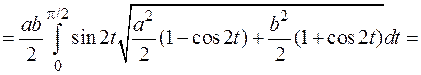
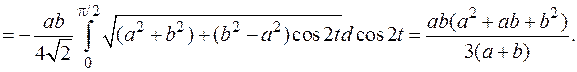
Задача 2. Вычислить 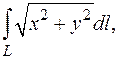 где
где  кривая, заданная уравнением
кривая, заданная уравнением 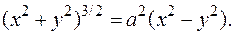
Решение. Перейдем к полярным координатам: 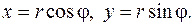 Уравнение кривой
Уравнение кривой  примет вид
примет вид 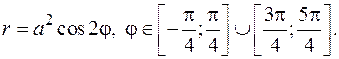 Для вычисления интеграла применим формулу (6.5). Так как
Для вычисления интеграла применим формулу (6.5). Так как 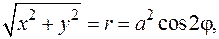
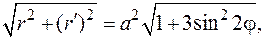 то
то

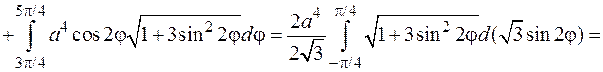
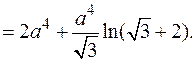
Задача 3. Найти массу  материальной кривой
материальной кривой  , заданной уравнением
, заданной уравнением  где
где 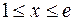 , если ее плотность
, если ее плотность 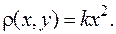
Решение. По формуле для массы  Для вычисления интеграла воспользуемся формулой (6.4). Так как
Для вычисления интеграла воспользуемся формулой (6.4). Так как
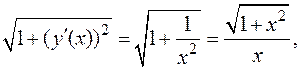
то 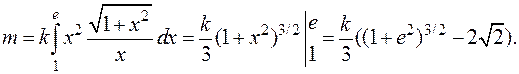
|
|
|


