 |
Уравнения, допускающие понижение порядка
|
|
|
|
Рассмотрим три наиболее распространенных вида дифференциальных уравнений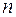 
-го порядка, допускающих понижение порядка.
a) Уравнение вида
. (8.6)
Общее решение получается с помощью 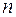-кратного интегрирования
,
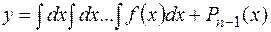где 
т.е. общий интеграл уравнения (8.6) есть сумма какого-либо частного решения этого уравнения и многочлена 
-й степени с произвольными постоянными коэффициентами.
Пример. Найти общее решение уравнения 
и его частное решение, удовлетворяющее условиям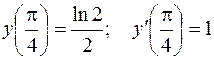 
.
Решение. Интегрируя первый раз, получим 
. Повторное интегрирование дает
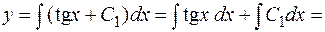
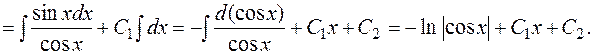
Следовательно, 
– общее решение. Подставив теперь в полученное общее решение и в выражение для первой производной значения 
и соответственно 
и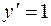 
, получим систему двух уравнений с неизвестными 
и 
:
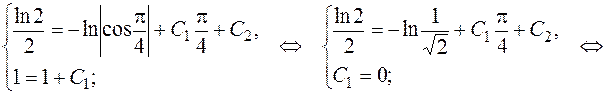
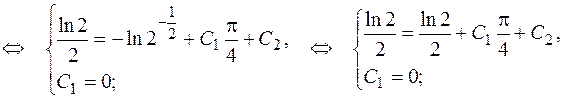
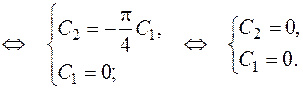
Подставив найденные и в общее решение, получим искомое частное решение 
, удовлетворяющее заданным начальным условиям.
б) Уравнение вида
. (8.7)
Уравнение (8.7) не содержит функции 
и ее нескольких последовательных производных 
. С помощью замены 
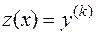понизим порядок уравнения на 
единиц: 
. Предположим, что для полученного уравнения общее решение имеет вид 
. Тогда искомая функция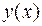 
получается с помощью 
кратного интегрирования функции 
.
Пример. Найти общее решение уравнения 
.
Решение. Данное уравнение не содержит и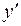 
. Положим 
, тогда 
и уравнение будет иметь вид: 
. Это линейное уравнение первого порядка (см. п. 7.6.). Его общее решение имеет вид 
. Так как 
, то для отыскания искомого общего решения надо проинтегрировать уравнение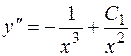 
. Таким образом,
,
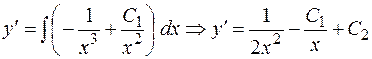тогда
.
Следовательно, 
, где 
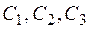– произвольные постоянные, является общим решением заданного уравнения.
в) Уравнения вида
. (8.8)
Уравнение (8.8) не содержит явно независимую переменную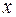 
. В этом случае примем за независимую переменную и введем новую функцию 
. Считая, что 
есть функция от и через посредство зависит от 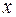и, применяя правило дифференцирования сложных функций, получим для производных функции по 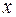выражения
|
|
|
,
,
аналогично вычисляются 
.
Подставляя в уравнение (8.8) вместо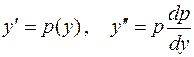 
и т.д., увидим, что в новых переменных порядок уравнения будет , т.е. на единицу ниже.
Если это преобразованное уравнение проинтегрировано и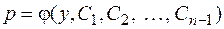 
– его решение, то нахождение общего интеграла данного уравнения сводится к интегрированию
.
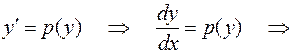
Откуда получаем общее решение ОДУ (8.8)
.
Пример. Найти общий интеграл уравнения 
.
Решение. Положим
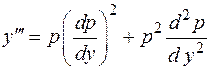и подставим в исходное уравнение, тогда получим
.
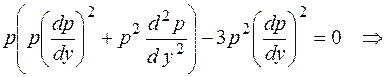
Сократим на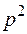 
, при этом учтем теряемое решение 
или 
и получим
.
Это уравнение рассматриваемого вида, делая ту же замену 
придем к уравнению 
.
Сократив на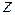 
(при этом учитываем еще одно решение 
, т.е. 
и 
), получим
.
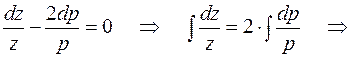
Проинтегрировав уравнение 
, находим 
, или 
.
Окончательно получим
, где 
.
Заметим, что в общее решение входят и потерянные ранее частные решения (кроме 
).
Задачи для самостоятельного решения
Задача. Решить дифференциальные уравнения, используя методы понижения порядка:
а) 
б) 
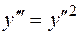в)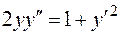 
Линейные однородные уравнения с постоянными
Коэффициентами
Общий вид линейного дифференциального уравнения порядка 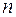с постоянными коэффициентами
, (8.9)
где 
– действительные постоянные.
Уравнение
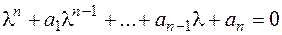, (8.10)
полученное заменой производных 
искомой функции степенями 
, называется характеристическим уравнением для уравнения (8.9).
Каждому действительному корню 
уравнения (8.10) кратности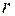 
соответствуют 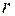линейно независимых решений уравнения (8.9)
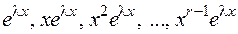, (8.11)
а каждой паре комплексных корней 
кратности 
соответствуют пар линейно независимых решений:
(8.12)
Линейная комбинация всех таких решений дает общее решение уравнения (8.9).
|
|
|
Запишем общее решение для случая 
. Рассмотрим уравнение
, (8.13)
где 
– действительные числа.
Характеристическое уравнение для (8.13) имеет вид
. (8.14)
Если квадратное уравнение (8.14) имеет два различных действительных корня 
и 
, то согласно (8.11) имеем два линейно независимых решения уравнения (8.13) 
и общее решение имеет вид
, (8.15)
где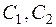 
– произвольные постоянные.
Если квадратное уравнение (8.14) имеет комплексные корни 
, тогда согласно (8.12) имеем два линейно независимых решения уравнения (8.13) 
и общее решение имеет вид
. (8.16)
Если квадратное уравнение (8.14) имеет два равных действительных корня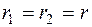 
, то согласно (8.11) имеем два линейно независимых решения уравнения (8.13) 
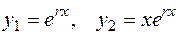и общее решение уравнения имеет вид
. (8.17)
Пример 1. Найти общее решение уравнения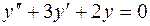 
.
Решение. Характеристическое уравнение 
имеет корни 
. Им соответствуют линейно независимые решения 
. Следовательно, общее решение имеет вид 
.
Пример 2. Найти общее решение уравнения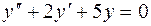 
.
Решение. Характеристическое уравнение имеет вид 
, его корни 
. Им соответствуют линейно независимые решения 
. Следовательно, общее решение имеет вид 
.
Пример 3. Найти общее решение уравнения 
.
Решение. Характеристическое уравнение 
имеет два равных действительных корня 
. Им соответствуют линейно независимые решения 
. Следовательно, общее решение имеет вид 
.
|
|
|
