 |
Команды преобразования выражений
|
|
|
|
Для некоторых команд Maple существуют две формы: активная и пассивная. Имя активной команды начинается со строчной буквы. После ввода такой команды и нажатия клавиши Enter, она сразу выполняется.

| Пассивная форма команды не выполняется немедленно ядром Maple, а просто в области вывода отображает математическую запись того, что она может сделать. Имя пассивной команды начинается с прописной буквы. В дальнейшем, используя команду value() пассивная команда может быть исполнена. Однако, основное предназначение пассивных команд - использование их как средства документирования производимых действий в обычной математической форме. |
В данном разделе лекции рассмотрен ряд наиболее часто используемых при выполнении аналитических вычислеий команд.
| < a)> | упрощение выражений |
| раскрытие скобок в выражении | |
| нахождение максимального числа независимых сомножителей выражения, линейных по заданным переменным с коэффициентами наиболее простой формы | |
| < a)> | сокращение алгебраической дроби |
| < a)> | приведение нескольких членов разложения к одному |
| приведение подобных членов | |
| рационализация дробей | |
| ограничения на неизвестные | |
| < B> | добавочные ограничения на неизвестные |
Рассмотрим более подробно эти команды.
Команда simplify() предназначена для упрощения разнообразных выражений, включающих рациональные дроби (алгебраические выражениия), содержащих тригонометрические, обратные тригонометрические функции, логарифмы, экспоненты и т.д..Эта команда имеет несколько форм вызова, отличающихся наличием параметров, управляющих процедурой упрощения. Её самый простой синтаксис имеет вид:
simplify(выражение);
|
|
|
В скобках в качестве параметра передается выражение, подлежащее упрощению.
Команда simplify() ищет в выражении вызовы функций, квадратные корни, радикалы и степени и инициирует подходящие процедуры упрощения, которые хранятся в основной библиотеке Maple.
В вызове команды можно задать конкретные процедуры упрощения, и могда только они будут использоваться для упрощения заданного выражения, а не весь возможный, установленный по умолчанию набор. Такой вызов обеспечивается следующей формой команды:
simplify(выражение, n1, n2...);
Здесь n1, n2... являются именами процедур упрощения: Ei, GAMMA, RootOf, @, hypergeom, ln, polar, power, radical, sqrt, trig и др.
В справке по команде simplify() можно найти перечень возможных процедур упрощения, а также полную информацию о формулах упрощения при использовании того или иного парметра (используя гиперссылки в системе помощи или набрав команду ?simplify[имя], где имя - одно из значений параметров функции).

| При упрощении выражения можно предположить, что на переменные в нем наложены некоторые ограничения. Это осуществляется заданием ключевого параметра assume=свойство. Форма вызова команды в этом случае имеет вид: |
simplify(выражение,assume=свойство);
где параметр свойство может принимать одно из следующих значений:
complex -комплексная область,
real - действительная область,
pozitiv - положительные действительные числа,
integer - целые числа,
RealRange(a,b) - интервал (a,b) действительных чисел.
При вызове команды упрощения сожно последним (или единственным, не считая самого упрощаемого выражения) параметром указать параметр с именем symbolic.

| В этом случае, если выражение содержит многозначные функции, то относительно них будет осуществлено формальное символическое упрощение. Отметим, что этот параметр надо использовать с осторожностью, так как в большинстве случаев результат упрощения не верен на всей комплексной плоскости, а также не всегда известно, какая ветвь многозначной функции использовалась при упрощении. |
Команда simplify() позволяет задать правила упрощения в виде равенств. Эти правила задаются вторым параметром функции в виде множества. Синтаксис команды в этом случае:
|
|
|
simplify(выражение,{равенство1. равенство2,...});
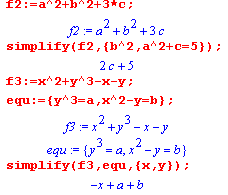
| Если какое-то выражение при упрощении должно равняться нулю, то такое правило можно задать, просто внеся выражение без знака равенства в список правил. Подробнее ознакомиться с использованием собственных правил упрощения можно на странице Справки, отображаемой командой?simplify[siderels] |
Основное назначение команды expand() - представить произведение в виде суммы, т.е. данная команда раскрывает скобки в алгебраическом выражении. Для частного двух полиномов (рациональная алгебраическая дробь) эта команда раскрывает скобки в числителе и делит каждый член полученного выражения на знаменатель, с которым она не производит никаких преобразований. Команда имеет следующий синтаксис:

| expand(ВЫРАЖЕНИЕ) expand(ВЫРАЖЕНИЕ, выр1, выр2,..., вырN) где ВЫРАЖЕНИЕ является выражением, в котром надо раскрыть скобки, выр1, выр2,..., вырN - необязательные параметры, указывают системе на подвыражения, в которых скобки раскрывать не надо. |
Данная функция знает правила преобразования тригонометрических выражений, выражений с экспоненциальными функциями, полиномами и др..
Основное предназначение команды factor() - разложение на множители полинома от нескольких переменных. Под полиномом в Maple понимается выражение, содержащее неизвестные величины, в которых каждый член представлен в виде произведения целых неотрицательных степеней неизвестных величин с числовым или алгебраическим коэффициентом, т.е. коэффициент может быть целым, дробным, с плавающей точкой, комплексным числом и даже представлять собой алгебраическое выражение с другими переменными.

| Синтаксис команды: factor(Выражение) factor(Выражение, пар) где необязательный второй параметр пар служит для указания, над каким числовым полем следует осуществлять разложение полинома. Он может иметь значения: real, complex, а также один радикал или список|множество радикалов. |
Если второй параметр не указан, команда factor() раскладывает полином на множители над числовым полем, которому принадлежат коэффициенты полинома.
|
|
|
При применинии команды factor() к алгебраической рациональной дроби (отношение двух полиномов) сначала осуществляется приведение дроби к нормальной форме (сокращение общих множителей числителя и знаменателя), а после этого и числитель, и знаменатель раскладываются на множители (с учетом поля коэффициентов).
Команда normal() приводит выражение, содержащее алгебраическую дробь, к общему знаменателю и упрощает полученную алгебраическую дробь, сокращая и числитель, и знаменатель на наибольший общий делитель. Команда имеет две формы вызова:

| normal(f); normal(Выражение, expanded); где параметр expanded служит для указания того, что после сокращения дроби в числителе и знаменателе раскрываются скобки. Если параметр Выражение задан в виде списка, множества, последовательности, ряда, уравнения, отношения, или функции, то команда normal(f) последовательно применяется к компонентам f. |
Команда combine() приводит несколько членов в выражении, представленном суммой, произведением или степенями неизвестных, к одному члену, используя разнообразные правила, которые по существу противоположны правилам, применяемым командой expand(). Команда имеет несколько форм вызова:
| combine(s) combine(s, пар) combine(s, пар, symbolic) где s - выражение, которое надо "свернуть" пар - необязательный параметр, который указывает на функции, правила преобразования которых (и только они!) должны применяться при выполнении команды. В качестве этого параметра могут быть использованы: | 
|
| abs | arctan | conjugate | exp |
| icombine | ln | piecewise | poligon |
| power | Psi | radical | range |
| Signum | trig |
symbolic - параметр, предписывающий команде combine() не обращать внимания на интервалы изменения аргументов (на ограничения значений аргументов) функций, указанных в качестве второго параметра. В этом случае осуществляется формальное символическое преобразование в соответствии с правилами преобразования этих функций.
Более подробную информацию об опциях команды combine() можно получить, выполнив команду ?combine[опция].
|
|
|
Команда collect() приводит подобные члены в обобщенных полиномах нескольких переменных, в которых в кчестве неизвестных могут выступать функции с аргументами, являющимися неизвестными величинами.

| Синтаксис этой команды имеет несколько форм: collect(выражение, x) collect(выражение, x, func) collect(выражение, x, alg, func) |
где x - параметр, указывающий на величину, относительно степени которой осуществляется приведение коэффициентов. Этот параметр может быть: именем неизвестной величины (x или y, или др.), списком или множеством в случае полинома нескольких переменных ([x,y,z] или {x,y,z}), именем функции с АРГУМЕНТОМ-неизвестной (exp(x) или cos(z)).
func - имя команды, которая применяется к полученным в результате коэффициентам при соответствующих степенях неизвестных. Обычно используются команды simplify или factor.

| alg - параметр, определяющий алгоритм приведения подобных членов для полиномов от НЕСКОЛЬКИХ переменных. Неизвестные, при степенях которых приводятся подобные члены, должны быть заданы в виде списка или множества.Этот параметр может принимать два значения: recursive (значение по умолчанию) или distributed. |
Параметр recursive инициирует следующий алгоритм: приводятся подобные члены при степенях первой неизвестной в СПИСКЕ, далее в полученных коэффициентах приводятся подобные члены относительно степеней второй неизвестной в списке и т.д. Если при использовании этого алгоритма параметр x представляет из себя МНОЖЕСТВО, то порядок приведения подобных членов определяется системой Maple и может меняться от сеанса к сеансу.
Параметр distributed указывает на приведение коэффициентов при членах, содержащих всевозможные произведения степеней неизвестных в списке или множестве, причем суммарная степень всех переменных возрастает от наименьшей к наибольшей.
Под рационализацией дробей понимается избавление от иррациональности в знаменателе. Команда rationalize() и производит именно такое преобразование над числовыми и алгебраическими дробями.
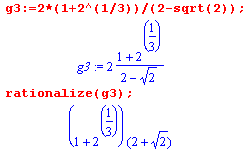
| Синтаксис команды: rationalize(F) где F - выражение или список выражений. |
| Эта команда может рационализировать алгебраическую дробь, знаменателькоторой содержит трансцендентные функции типа sin(), ln(), exp() и т.п.. Однако, если агрумент этих функций является дробью с иррациональностями в знаменателе, то эти конструкции не участвуют в прцессе рационализаци. | 
|
Зачастую без введения определенных ограничесний на некоторые выражения ничего нельзя сказать о свойствах математических объектов, в которых они фигурируют. Одни ограничения вытекают из области определения независимых переменных, другие мы накладываем сами в процессе решения задачи. Команда assume() накладывает ограничесния на неизвестные величины Maple. Синтаксис команды:
|
|
|
Assume(x, свойство)
Здесь x -любая неопределенная переменная Maple или выражение с такими переменными.
свойство - параметр, принимающий значения, равные названиям свойств (зарезервированные символьные имена Maple), имени типа данных или числовому диапазону.
Некоторые свойства числовых переменных и выражений:
| Название свойства | Описание |
| negative | Отрицательные вещественные числа (нуль не включается) |
| nonnegative | Неотрицательные вещественные числа (нуль включается) |
| positive | Положительные вещественные числа (нуль не включается) |
| natural | Натуральные числа (целые, большие или равные нулю) |
| posint | Целые строго больше нуля |
| odd | Нечетные числа |
| even | Четные числа |
| complex | Комплексные числа |
| NumeralNonZero | Комплексные числа, исключая 0 |
| real | Вещественные числа |
| rational | Рациональные числа (дроби и целые) |
| irrational | Иррациональные числа |
| integer | Целые числа |
| fraction | Только дробные числа |
| prime | Простые числа |
Пару параметров (x, свойство) можно заменить математическим отношением, если, конечно, это возможно. Например, (x, negative) соответсвует отношению (x<0). Команда assume() может получать несколько пар (х, свойство) или математических отношений в качестве своих параметров. В этом случае все заданные ограничения действуют одновременно.

| НОВОЕ ограничение, накладываемое новой командой assume() на переменную, ОТМЕНЯЕТ все предыдущие ограничения. Если по ходу решения задачи необходимо постепенно добавлять ограничения на переменную, то используют команду additionaly(), параметры которой полностью соответствуют параметрам команды assume(). |
Если на переменную наложены ограничения, то в области вывода в выражении с этой переменной сразу же за её именем по умолчанию отображается символ тильда (~). Эту функциональность можно изменить, используя команды основного меню Options -> Assumed Variables. При выборе подкоманды No Annotation пользователь вообще не будет информирован об ограничениях, переменная с ограничениями будет продолжать отображаться как и все переменные без ограничений. Подкоманда Phrase отображает в области вывода словесное сообщение о том, что на переменную наложены ограничения. А подкоманда Trailing Tildes позволяет включить режим отображения переменных с наложенными ограничениями, если он был отключен.
Отобразить информацию о наложенных на неизвестную величину ограничениях можно с помощью команды about(x).
Дополнительные функции, позволяющие получить информацию о переменных:

|
|
- coulditbe(переменная, свойство) - функция проверяет, может ли заданная переменная соответствовать заданному свойству. Она возвращает true, если хотя бы одно из возможных значений переменной может иметь заданное свойство, и false в противном случае. Смысл значения FAIL тот же, что и для предыдущей функции
Пакеты Maple
Обзор пакетов Maple
Встроенные в Maple пакеты позволяют выполнятьматематические построения и преобразования, начиная от элементарной математикии заканчивая общей теорией относительности.
Для того, чтобы использовать команды какого-нибудб пакета, необходимо подключить его или целиком, или только требуеме команды этого пакета (см. Лекцию 1).
В таблице, приведенной ниже, содержится список всех пакетов Maple с их кратким описанием:
| Пакет | Содержит |
| algcurves | Средства для изучения однормерных алгебраических кривых, определяемых полиномами нескольких переменных. |
| codegen | Средства для создания, обработки и перевода процедур Maple в код языков программирования С и Fortran. |
| combinat | Комбинаторные функции, включая вычисление перестановок и сочетаний. В настоящее время считается устаревшим. Ждя этих же целей рекомендуется использовать пакет combstruct. |
| combstruct | Команды для работы с комбинаторными структурами. |
| context | Средства для построения и изменения контекстных меню в графическом интерфейсе пользователя. |
| DEtools | Средства для выполнения преобразований обыкновенных дифференциальных уравнений, их решения и графического отображения решений с возможностью построения фазовых портретов и полей направлений систем дифференциальных уравнений. |
| diffalg | Команды для работы с системами полиномиальных дифференциальных уравнений, как обыкновенных, так и в частных производных. |
| difforms | Команды для работы с дифференциальными формами при решении задач дифференциальной геометрии. |
| Domians | Команды для создания областей вычисления. Поддерживают работу с полиномами, матрицами и рядами над числовыми кольцами, конечными полями, кольцами полиномов и матриц. |
| finance | Команды для выполнения финансовых вычислений (финансовая математика). |
| GaussInt | Команды для работы с гауссовыми целыми числами - комплексными числами вида a + b I, где a и b целые. |
| genfanc | Команды для работы с рациональными производящими функциями. |
| geom3d | Команды для выполнения построений и вычислений в трехмерном евклидовом пространстве. Позволяют строить и работать в трехмерном пространстве с точками, линиями, плоскостями, треугольниками, сферами и т.д. |
| geometry | Команды для выполнения построений и вычислений нам евклидовой плоскости. Позволяют строить и работать с точками, линиями, плоскостями, треугольниками, окружностями и т.д. |
| GF | Команды для работы с полями Галуа. |
| Groebner | Команды для организации вычислений в базисе Гренбера. |
| group | Команды для работы с группами перестановок и конечными группами. |
| inttrans | Команды для работы с интегральными преобразованиями и их обратными преобразованиями. |
| linesumm | Команды определения симметричности ссистем дифференциальных уравнений в частных производных. |
| linalg | Команды для работы с символьными матрицами и векторами: сложени, умножение матриц, собственные числа и векторы в символьном виде и др. |
| LinearAlgebra | Усовершенствованные команды линейной алгебры для работы со специальным видом числовых матриц Matrix. |
| LREtools | Команды для преобразования, графического отображения и решения рекуррентных уравнений. |
| Matlab | Команды для подключения и использования некоторых матричных функций системы численных вычислений Matlab. Работают при установленном пакете Matlab. |
| networks | Команды для создания работы с различными типами графов. |
| numapprox | Команды для построения полиномиальной аппроксимации функций на заданном интервале. |
| numtheory | Команды для вычислений в области классической теории чисел. |
| Ore_algebra | Команды для основных вычислений в алгебрах линейных операторов. |
| orthopoly | Команды построения различных типов ортогональных полиномов. |
| padic | Команды p- адического приближения вещественных чисел. |
| PDEtools | Средства для выполнения преобразований дифференциальных уравнений в частных производных, их решения и графического отображений решений. |
| plots | Команды построения специальных видов графиков функций, включая построение линий уровня, отображение неявно заданных функций, включение текстовых надписей в график, построение графиков в различных системах координат. |
| plottools | Команды для создания и работы с графическими объектами. |
| polytools | Команды для работы с полиномами. |
| powseries | Команды построения и работы с формальными степенными рядами. |
| process | Команды, позволяющие писать многопроцессорные Maple-программы в системе UNIX. |
| simplex | Команды решения задач линейной оптимизации на основе симплекс-метода. |
| Slode | Команды построения формального решения линейных обыкновенных уравнений в виде степенных рядов. |
| Spread | Команды, позволяющие программировать электронные таблици Maple. |
| stats | Команды статистической обработки данных |
| student | Команды,наиболее часто используемые студентами (?) |
| sumtools | Команды вычисления конечных и бесконечных сумм. |
| tensor | Команды работы с тензорами и их пременение в общей теории относительности. |
В предлагаемом курсе рассматриваются несколько пакетов, наиболее полезных, с нашей точки зрения, для выполнения студентами курсовых и дипломных работ. В этой лекии рассматриваются пакеты linalg, LinearAlgabra и student. Пакеты DEtools и PDEtools рассмотрены в Лекции 6, графическим пакетам plots и plottools - посвящена часть Лекции 7.
В Maple 6 выполнение преобразований линейной алгебры можно осуществлять с помощью команд двух пакетов: linalg и LinearAlgabra, функциональность которых практически одинакова. Первый пакет входил в состав всех предыдущих версий Maple, тогда как второй пакет - это новое средство, позволяющее работать с числовыми матрицами, в том числе и с матрицами больших размеров, используя всю мощь известного пакета численных расчетов NAG (Numerical Algorithms Group).
Основными объектами, с которыми работают команды этих пакетов, являются матрицы, однако матрицы одного пакета не эквивалентны матрицам другого. В пакете linalg используются матрицы, построенные на основе массива, создаваемого командой array(), тогда как в пакете LinearAlgabra применяются векторы и матрицы, построенные на основе новой структуры r-таблицы (r-table) и создаваемые специальными конструкторами Vector() и Matrix() или с использованием краткой нотации < a, b, c >. Матрицы в пакете linalg вычисляются только до уровня своих имен, поэтому в нем невозможно вычислить операции поэлементного суммирования или вычитания, используя постые операции над идентификаторами матриц, и приходится пользоваться специальной командой evalm() для вывода результирующих матриц. В пакете LinearAlgebra матрицы вычисяются до уровня своих элементов, поэтому простое задание имени матрицы в области ввода рабочего листа приводит к отображению ее элементов, а не имени матрицы, как в случае с пакетом linalg. Кроме этого, в пакете LinearAlgebra матрицы могут задаваться в качестве операндов сложения и вычитания, что приводит к поэлементному выполнению указанных операций без использования дополнительных команд.
При выборе пакета линейной алгебры для работы рекомендуется принять во внимание следующее:
- Пакет linalg полезен при выполнении абстрактных вычислений над матрицами и векторами.
- Пакет LinearAlgebra обладает более дружественным интерфейсом и особенно эффективен при работе с ЧИСЛОВЫМИ матицами больших размеров из-за возможности обращения к откомпилированным программам пакета численных расчетов NAG.
Пакет linalg
Пакет линейной алгебры linalg содержит команды создания матриц и векторов, предлагает большой набор функций для работы со структурой этих объектов, для выполнения основных матричных и векторных операций и для решения основных задач линей ной алгебры: решение систем линейеых уравнений, нахождение собственных значений и собственных векторов матрицы, приведение матриц к спкциальным формам и т.д. И все эти действия можно выполнять с матрицами и векторами, элементами которых являются общие алгебраические выражения, получая результаты такде в виде алгебраических выражений.
Определить матрицу или вектор в Maple можно двумя способами: либо с помощью команды array () стандартной библиотеки, либо командами matrix() и vector() (см Лекцию 2).
Команды для работы со структурой векторов и матриц:
| rowdim(M) | Количество строк матрицы M |
| coldim(M) | Количество столбцов матрицы M |
| vectdim(V) | Количество элементов вектора V |
| delrows(M, i..j) | Удаление из матрицы M строк с номерами от i до j |
| delcols(M, i..j) | Удаление из матрицы M столбцов с номерами от i до j |
| extend (M, Nr, Nc, expr) | Добавление строк и столбцов в матрицу M. Здесь Nr и Nc -целые числа (включая 0),представляют количество добавляемых строк и столбцов; expr - выражение, котороеиспользуется в качестве значений добавляемых элементов строк и столбцов |
| row(M,i) | Выделение строки с номером i из матрицы М. |
| col(M,j) | Выделение столбца с номером j из матрицы М. |
| submatrix (M, i1..i2, j1..j2) | Выделение подматрицы, состоящей из элементов столбцов с номерами от i1 до i2 и строк с номерами от j1 до j2 |
| subvector(V, i1..i2) | Выделение вектора, состоящего из из элементов с номерами от i1 до i2 |
| minor(M, i, j) | Матрица минора элемента с индексами (i, j) |
|
|
|


