 |
I. Надежность машин и критерии работоспособности.
|
|
|
|
Надежность – свойство оборудования выполнять безотказно работу в течение положенного срока эксплуатации.
Надежность является величиной вероятностной, т.е. оценивается вероятностью безотказной работы. Например, вероятность безотказной работы P некоторой партии машин рассчитывается по формуле:
,
где N – общее число машин партии;
N0 – количество машин, вышедших из строя.
Пусть N 0 равно 100, N – 10, тогда P равно:
Чаще надежность оценивается частотой отказов λ, т.е. числом машин, вышедших из строя в течение работы:
где τ – срок эксплуатации изделия.
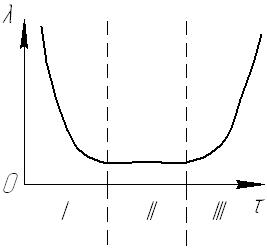
Рис. I. 1
Значение λ меняется во времени (Рис. I.1), в связи с чем срок эксплуатации изделия можно разделить на 3 периода, каждому из которых соответствует свой режим работы. Резкое уменьшение λ в I режиме обусловлено наладкой и запуском оборудования, II режим определяется значительным периодом работы оборудования с малым числом отказов, резкое увеличение λ в III режиме связано с большим числом отказов в связи с износом оборудования.
Надежность работы определяется рядом критериев работоспособности, из которых основными являются прочность, жесткость, коррозийная стойкость, эрозия, виброустойчивость, ремонтноспособность и критерий соответствия оборудования требованиям GMP (Международный Стандарт Культурного Проектирования). Прочность – свойство детали работать без разрушения в течение всего срока эксплуатации. Расчет детали на прочность обычно сводится к выполнению условия статической прочности – действительные напряжения σ и τ не должны превышать допустимой величины [ σ ] и [ τ ] соответственно:
и условия динамической прочности:
|
|
|
,
где n – общий коэффициент запаса прочности.
Жесткость – свойство детали сопротивляться деформациям. Расчет детали на жесткость сводится к выполнению условия жесткости. Для вала таким условием является соотношение:
,
где φ – угол поворота вала при кручении.
Критерий жесткости связан с показателем устойчивости. Устойчивость – способность детали сохранять свою исходную геометрическую форму. К изменению исходной формы, т.е. к смятию оболочки, приводит внешнее давление, действующее на оборудование (Рис. I. 2).
Рис. I. 2
В химической промышленности необходимым условием длительной работы оборудования является способность материала противостоять химически-агрессивным средам, которое оценивается коррозийной стойкостью.
Коррозийная стойкость – свойство материала детали работать длительное время без разрушения в химически-агрессивной среде.
Расчетов на долговечность по коррозии нет. При конструировании детали обычно используют добавку С к толщине стенки, что учитывается скоростью образования коррозии П и временем эксплуатации τ:
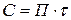
В связи с этим рассматривают несколько групп материалов:
- стойкие материалы, которые ржавеют, т.е. утончаются со скоростью около 0,001 миллиметра в год;
- средние группы, где П не превышает 0,1 мм/год.
Однако у некоторых материалов П достигает нескольких миллиметров в год.
Эрозия – некоторое уменьшение толщины стенки вследствие гидромеханического истирания (например, в результате вращения мешалки перемешивающего устройства).
Как правило, машины работают в условиях вибронагружения, поэтому немаловажным условием прочности является виброустойчивость.
Виброустойчивость – способность детали работать в условиях динамического (меняющегося во времени) напряжения без значительных амплитуд вибраций.
Виброустойчивость продолжается до тех пор, пока не возникает амплитуда, при которой происходит совпадение собственной частоты ω с критической частотой ωкр, возникающей в процессе работы. Их совпадение приводит к появлению резонанса, что влечет за собой возрастание амплитуды. Для вращающихся валов существует критическая угловая скорость, при которой возникают опасные резонансные колебания, т. е. амплитуда вибрации зависит от частоты колебаний, являющейся функцией:
|
|
|
,
где Сp – жесткость конструкции вала;
m – масса вала, кг.
Рис. I. 3
Во избежание нежелательных уровней амплитуд колебаний выбирают рабочую угловую скорость из условия виброустойчивости вала (Рис. I. 3):
II. Нагрузки
Разнообразие тел с различными габаритными параметрами можно свести к трем основным типам. Для определения каждого из таких типов рассмотрим тело (Рис. II. 1).
Рис. II. 1
В зависимости от соотношений величин размеров х1, х2 и х3 тела делятся на:
- балка, у которой х1 >> х2, х3 ;
- плита (или пластина), у которой х3, х1 >> х2;
- массив, где х1 ~ х2 ~ х3 .
Все нагружения (нагрузки) – силы, действующие на тело, - рассматриваются как внешние и внутренние. Последние, в свою очередь, делятся на активные и реактивные силы, которые обусловлены требованиями условия эксплуатации. Возникновение внутренних силовых факторов связано со стремлением материала сохранять свое первоначальное состояние. Внутренние силовые факторы могут быть статическими, когда влияние силы или момента сил не изменяется в течение времени, и динамическими, когда силовые факторы изменяются во времени. В зависимости от площади поверхности действия, силы делят на концентрированные (приложенные к точке или малой поверхности детали) и распределенные по объему поверхности или длине детали.
А) б)
Риc. II. 2
Внешние силы F i задаются из условий эксплуатаций, либо определяются уравнениями равновесия для данной детали. В то же время внутренние усилия Q i определяются с использованием метода сечений, который сводится к тому, что деталь мысленно рассекается на части, и рассматривается выделенная часть в равновесии под действием внешних и внутренних сил (Рис. II. 2, а). Поскольку вся деталь находится в равновесии, то и выделенная часть этой детали находится в равновесии, что обеспечивает взаимодействие внешних и внутренних силовых факторов, при этом внутренние силы рассматриваются в приложении относительно выбранных осей координат. К примеру, горизонтальное равновесие обеспечивается комплексом внешних и внутренних сил (Рис. II.2, б), неопрокидывание условливается моментом кручения Т – суммой моментов внутренних сил относительно оси 0z, условием неповорота вокруг осей 0х и 0у является сумма моментов внутренних и внешних сил относительно оси 0х и 0у соответственно. Таким образом, условие равновесия описывается шестью уравнениями:
|
|
|
- продольное равновесие;
- поперечное равновесие относительно оси 0у;
- поперечное равновесие относительно оси 0у;
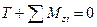- условие неопрокидывания;
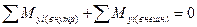- условие неповорачивания вокруг оси 0у;
- условие неповорачивания вокруг оси 0х;
Физический смысл метода сечений сводится к тому, что равновесие выделенного участка рассматривается под действием внешних и внутренних силовых факторов. Однако на практике редко используют систему из шести уравнений (объясняется неудобством решения данной системы), поэтому обычно рассматривают отдельные случаи:
- если N не равно 0, все остальные силовые факторы нулевые, то это случай сжатия или растяжения;
- если Qx, Qy не раны 0, то это случай среза;
- если Mz и Т не равны 0, то это означает, что деталь подвержена чистому кручению;
- если Mуi(внутр.) и Mуi(внешн..) не равны 0, тогда равновесие обеспечивает чистый изгиб. 
На практике чаще наблюдается случай сложного нагружения.
А) б)
Рис. II. 3
Наличие внутренних силовых факторов приводит к тому, что в сечении возникает механическое напряжение Р – удельная сила, мера интенсивности нагружения детали (Рис. II.3, а). Напряжение Р определяется как векторная сумма векторов всех непрерывно распределенных по сечению внутренних сил, т.е. Р – внутреннее усилие сечения. Удельная величина p:
,
где А – площадь поперечного сечения детали.
Для удобства Р раскладывается на проекции на основные оси: σ - нормальное напряжение, τ - касательное напряжение (Рис. II.3, а).
|
|
|
.
Рассмотрим нагружение на наклонной площадке (Рис. II.3, б). Величина напряжения зависит от ориентации сечения, так как величина площади сечения является функцией угла α:
.
Так, для балки с площадью А поперечного сечения при действии некоторой силы F напряжение ρ равно:
,
где N – реактивная сила, тогда:
.
При разложении вектора ρ на проекции σα и τα, получим:
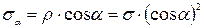(II. 1)
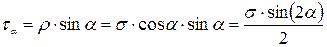. (II. 2)
Используя формулы (II. 1) и (II. 2), определим максимальные значения нормального (σα) и касательного (τα) напряжений. Очевидно, что σα максимально, если косинус угла α равен единице, тогда α равен нулю, т.е.:
.
Аналогично, при 
, т.е. 
,
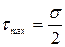т.е. внутри структуры любого материала имеется множество площадок, каждая из которых имеет свое напряжение. Образец такого материала при разрушении «скашивается» под углом 45º (Рис. II. 4).
Рис. II. 4
|
|
|
