«Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им.В.И. Ульянова (Ленина)»

МИНОБРНАУКИ РОССИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)»

(СПбГЭТУ «ЛЭТИ»)

В. М. Пухова

МАТЕМАТИКА, ФИЗИКА, ИНФОРМАТИКА:

основные определения и понятия дисциплин

 

 

Учебное пособие

для слушателей подготовительного отделения ИНДЕК

 

Санкт-Петербург

Оглавление

Математика. 3

Арифметика. 3

Алгебра. 6

Геометрия. 13

Тригонометрия. 17

Высшая математика. 20

Физика. 23

Кинематика. 23

Динамика. 28

Статика. 31

Гидростатика. 33

Законы сохранения в механике. 34

Колебательные движения и волны.. 36

Молекулярная физика. 39

Термодинамика. 45

Информатика. 51

Представление информации и операции над информацией. 51

Алгебра логики. 54

Теория алгоритмов. 58

Основы устройства ЭВМ.. 62

Список литературы.. 68

Математика

Математика – это фундаментальная наука, предметом изучения которой являются величины, количественные отношения, а также пространственные формы. Базовыми разделами математики являются: арифметика, алгебра, геометрия, тригонометрия, высшая математика.

Арифметика

Арифметика – это раздел математики, предметом изучения которого являются числа, их отношения и свойства.

Цифра – это специальный знак, который входит в кодовый набор системы счисления и используется отдельно или в группе для обозначения числа. Например, арабские цифры включают десять однозначных цифр, от 0 до 9.

Число – это основное понятие математики, обозначающее величину, при помощи которой производится счёт. Например, 23 – это число, составленное из цифр 2 и 3.

Сложение чисел – это одно из основных арифметических действий для двух чисел, которые в этом случае называются слагаемыми. Результатом сложения чисел является новое число, которое называется сумма. Сумма получается в результате увеличения первого слагаемого на значение второго слагаемого. Запись сложения чисел: , где  и  – это слагаемые, а  – это сумма.

Вычитание чисел – это одно из основных арифметических действий для двух чисел, которые в этом случае называются уменьшаемое и вычитаемое. Результатом вычитания чисел является новое число, которое называется разность. Разность получается в результате уменьшения уменьшаемого на значение вычитаемого. Запись вычитания чисел: , где  – это уменьшаемое,  – это вычитаемое, а  – это разность. Вычитание – это обратная сложению операция.

Умножение чисел – это одно из основных арифметических действий для двух чисел, которые в этом случае называются сомножителями, причём первый сомножитель иначе называется множимое, а второй сомножитель иначе называется множитель. Результатом умножения чисел является новое число, которое называется произведение. Произведение получается в результате последовательного многократного сложения множимого числа с самим собой в количестве раз равное множителю. Запись умножения чисел: , где  и  – это сомножители, а  – это произведение. Умножение чисел – это многократное сложение.

Деление чисел – это одно из основных арифметических действий для двух чисел, которые в этом случае называются делимое и делитель. Результатом деления чисел является новое число, которое называется частное. Частное получается в результате последовательного многократного вычитания делителя из значения делимого и равно количеству проведённых вычитаний, причём, если делимое становится меньше делителя, то вычитание прекращается, а это число называется остаток (остаток от деления). Запись деления чисел (с остатком): , где  – это делимое,  – это делитель,  – это частное, а  – это остаток. Деление – это обратная умножению операция.

Основные свойства арифметических действий:

· коммутативность сложения: 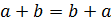, а значит, от перестановки слагаемых сумма не меняется (переместительный закон сложения),

· коммутативность умножения: 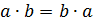, а значит, от перестановки сомножителей произведение не меняется (переместительный закон умножения),

· ассоциативность сложения: , а значит, сумма не зависит от порядка вычисления (сочетательный закон сложения),

· ассоциативность умножения: 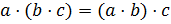, а значит, произведение не зависит от порядка вычисления (сочетательный закон умножения),

· дистрибутивность сложения относительно умножения: , а значит, произведение числа на сумму двух чисел можно заменить суммой двух произведений, и наоборот (распределительный закон).

Противоположное число – это такое число противоположное исходному ненулевому числу, которое при сложении с исходным числом даёт ноль. Например, для числа 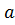 противоположным числом является .

Множество – это набор элементов, которые объединены общим признаком.

Натуральные числа  – это множество чисел, которое используются для счёта предметов.

Чётные числа – это натуральные числа, которые делятся на 2 без остатка, например, число 6.

Нечётные числа – это натуральные числа, которые не являются чётными числами, например, число 5.

Простые числа – это натуральные числа, которые имеют два различных делителя таких, что они делятся на них без остатка. Иными словами, это натуральные числа, которые без остатка делятся на само себя и на единицу, например, число 11. Число 1 простым числом не является.

Составные числа – это натуральные числа, которые не являются простыми числами, например, число 4. Число 1 составным числом не является.

Целые числа  – это множество чисел, которое включает в себя натуральные числа, им противоположные числа и ноль.

Дробь – это число, которое состоит из одной или нескольких равных частей целого. Целые числа являются частным случаем дробей. Дроби бывают обыкновенными (например, ) и десятичными (например, 0, 75).

Обыкновенная дробь – это дробь, которая записывается в виде , где z – это целое число, n – это натуральное число. Число над чертой называется числителем и является делимым, а число под чертой называется знаменателем и является делителем. Всякая обыкновенная дробь может быть представлена определённым образом в виде конечной десятичной дроби (например, 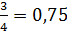) или в виде бесконечной периодической десятичной дроби (например, ).

Основные свойства обыкновенных дробей:

· значение дроби не меняется при умножении (или делении) числителя и знаменателя дроби на одно ненулевое число: ,

·  можно складывать (вычитать) только дроби, которые имеют одинаковый знаменатель. Результатом сложения (вычитания) дробей является дробь, числитель которой равен сумме (разности) числителей исходных дробей, а знаменатель остаётся неизменным: ,

·  результатом умножения дробей является дробь, числитель которой равен произведению числителей исходных дробей, а знаменатель равен произведению знаменателей исходных дробей: ,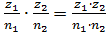

·  результатом деления дробей является дробь, числитель которой равен произведению числителя одной дроби на знаменатель другой, а знаменатель равен произведению знаменателя одной дроби на числитель другой: . Деление дробей можно заменить умножением одной дроби на дробь обратную другой дроби.

Процент  – это одна или несколько сотых частей целого. Процент обозначается знаком «%». Например, 2% означают 0, 02 доли целого.

Обратное число – это такое число обратное исходному ненулевому числу, которое при умножении на исходное число даёт единицу. Например, для числа 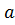 обратным числом является .

Пропорция – это равенство отношений пар чисел. Пропорция имеет вид a: b=c: d, что обозначает: a так относится к b, как c относится к d, и это постоянное отношение называется коэффициентом пропорциональности. В пропорции числа a и d – это крайние члены пропорции, а числа b и c – это средние члены пропорции. Произведение крайних членов пропорции равно произведению средних членов пропорции. Две величины находятся в прямой пропорциональной зависимости, если при увеличении (уменьшении) одной из них в несколько раз, другая увеличивается (уменьшается) в равное количество раз. Две величины находятся в обратной пропорциональной зависимости, если при увеличении (уменьшении) одной из них в несколько раз, другая уменьшается (увеличивается) в равное количество раз.

Рациональные числа 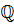 – это множество чисел, каждое из которых можно представить в виде обыкновенной дроби. Рациональные числа включают в себя целые числа.

Иррациональные числа – это множество чисел, каждое из которых не является рациональным, а значит, их невозможно представить в виде обыкновенной дроби, но можно представить в виде бесконечной непериодической десятичной дроби (например, число π =3, 1415926…).

Действительные (вещественные) числа 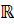 – это множество чисел, которое включает в себя рациональные и иррациональные числа.

Числовая ось – это прямая, на которой изображаются все действительные числа. Числовая ось задаётся выбором положительного направления, точки начала отсчёта, и единицы масштаба (единичного отрезка) на любой прямой. Положительные числа на числовой прямой располагаются в стороне положительного направления числовой прямой, ноль располагается в точке начала отсчёта. Отрицательные числа располагаются симметрично относительно точки начала отсчёта равным им по значению положительным числам.

Модуль числа – это неотрицательное число, которое равно расстоянию на числовой оси между числом и точкой начала отсчёта. Запись модуля числа: .

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: