 |
Тригонометрия
|
|
|
|
Тригонометрия – это раздел математики, предметом изучения которого являются тригонометрические функции, их отношения и свойства, и их использование в геометрии.
Тригонометрическая функция – это функция, которая определяет зависимость длин сторон прямоугольных треугольников от величин острых углов. В прямоугольном треугольнике две стороны, которые образуют прямой угол треугольника, называются катеты, а сторона, которая лежит напротив прямого угла, называется гипотенуза. Аргументом тригонометрической функции является угол, который может быть выражен произвольным числом в градусах (°) или радианах (рад).
Синус – это тригонометрическая функция, которая определяет зависимость длины катета b прямоугольного треугольника от величины острого угла 
, который образован другим катетом и гипотенузой длиной с. Синус угла обозначается 
и определяется отношением длин лежащего напротив угла катета b и гипотенузы: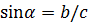 
. В декартовой системе координат синус – это проекция вектора, модуль которого равен единице, на ось координат y.
Косинус – это тригонометрическая функция, которая определяет зависимость длины катета a прямоугольного треугольника от величины острого угла , который образован данным катетом и гипотенузой длиной с. Косинус угла обозначается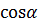 
и определяется отношением длин прилежащего к углу катета 
и гипотенузы: 
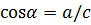. В декартовой системе координат косинус – это проекция вектора, модуль которого равен единице, на ось координат x.
Основное тригонометрическое тождество – это соотношение, которое устанавливает зависимость между синусом и косинусом угла и имеет вид: 
.
Тангенс – это тригонометрическая функция, которая определяет зависимость длин катетов прямоугольного треугольника 
от величины острого угла , который образован катетом длиной a и гипотенузой длиной с. Тангенс угла обозначается 
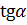и определяется отношением длин лежащего напротив угла катета b и прилежащего к углу катета a: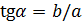 
. Тангенс угла связан с его синусом и косинусом соотношением: 
|
|
|
Котангенс – это тригонометрическая функция, которая определяет зависимость длин катетов прямоугольного треугольника от величины острого угла , который образован катетом длиной a и гипотенузой длиной с. Котангенс угла обозначается 
и определяется отношением длин прилежащего к углу катета a и лежащего напротив угла катета b: 
. Котангенс угла связан с его синусом и косинусом соотношением: 
Теорема синусов – это теорема, которая определяет зависимость длин сторон любых треугольников от величин углов этих треугольников. В треугольнике с углами равными 
и длинами сторон, которые лежат напротив этих углов, равными 
, соответственно, теорема синусов имеет вид: 
.
Теорема косинусов – это теорема, которая определяет зависимость длин сторон любых треугольников от величин углов этих треугольников. В треугольнике с углами равными и длинами сторон, которые лежат напротив этих углов, равными , соответственно, теорема косинусов имеет вид: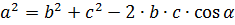 
, 
, 
.
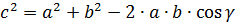Формулы приведения – это соотношения, которые устанавливают зависимости между тригонометрическими функциями различных острых углов при добавлении к ним фиксированного угла. Формулы приведения в общем случае определяются соотношением: 
, где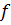 
– это тригонометрическая функция, 
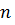– это целое число.
Основные формулы приведения для синуса острого угла α :
· 
· 
· 
· 
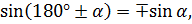
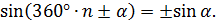
Основные формулы приведения для косинуса острого угла α :
· 
· 
· 
· 
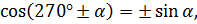
Формулы сложения – это соотношения, которые устанавливают зависимости между тригонометрическими функциями суммы и разности различных углов и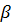 
.
|
|
|
Основные формулы сложения:
· 
,
· 
,
· 
· 
Формулы двойного угла – это соотношения, которые устанавливают зависимости между тригонометрическими функциями суммы различных углов и 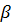, когда 
Основные формулы двойного угла:
· 
,
· 
,
· 
,
· 
.
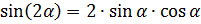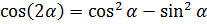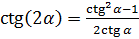Обратная тригонометрическая функция – это функция, являющаяся обратной к данной тригонометрической функции (аркфункция). Обратная тригонометрическая функция данного числа – это значение угла в радианах такое, что тригонометрическая функция угла равна данному числу.
Арксинус – это обратная тригонометрическая функция данного числа, численно равная такому значению угла в радианах, что синус угла равен данному числу. Арксинус числа x обозначается 
.
Арккосинус – это обратная тригонометрическая функция данного числа, численно равная такому значению угла в радианах, что косинус угла равен данному числу. Арккосинус числа x обозначается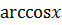 
.
Арктангенс – это обратная тригонометрическая функция данного числа, численно равная такому значению угла в радианах, что тангенс угла равен данному числу. Арктангенс числа x обозначается 
.
Арккотангенс – это обратная тригонометрическая функция данного числа, численно равная такому значению угла в радианах, что котангенс угла равен данному числу. Арккотангенс числа x обозначается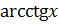 
.
|
|
|
