Высшая математика

Высшая математика – это раздел математики, в котором изучаются векторная алгебра, аналитическая геометрия, математический анализ.

Аналитическая геометрия – это раздел высшей математики, в котором изучаются геометрические свойства векторов.

Вектор – это абстрактный математический объект, который характеризуется числовым значением (длина, модуль или величина вектора), направлением в пространстве и точкой приложения вектора (начало вектора). С точки зрения геометрии, вектор – это отрезок прямой, для которого указана какая из его крайних точек является началом, а какая является концом, то есть он определяется как направленный отрезок. В заданной системе координат вектор однозначно определяется набором координат. Если начало вектора – это точка A, а конец вектора – это точка B, то вектор обозначается . Знать вектор – это значит, знать его числовое значение и направление в пространстве. Последнее требование отличает векторную величину от обычной скалярной величины, для которой достаточно знать только её числовое значение.

Координаты вектора – это упорядоченный набор величин, которые определяют вектор в заданной системе координат. Координаты вектора в прямоугольной системе координат равны разности соответствующих координат точек конца и начала вектора. Например, если начало вектора – это точка 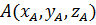, а конец вектора – это точка 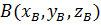, то вектор

Модуль вектора – это числовое значение вектора, которое определяет его длину, то есть длину отрезка прямой между началом и концом вектора. Модуль вектора  обозначается 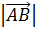 и является скалярной величиной, причём если начало вектора – это точка 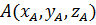, а конец вектора – это точка 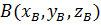, то .

Угол между векторами – это наименьший угол, который образуют два вектора при условии, что начала обоих векторов совпадают. Угол между векторами  обозначается  и находится в пределах от 0° до 180°.

Проекция вектора на ось координат – это число, которое равно произведению модуля вектора на косинус наименьшего угла между вектором и осью координат.

Ортогональные векторы – это векторы, угол между которыми равен 90°. Такие векторы иначе называются перпендикулярные векторы.

Коллинеарные векторы – это векторы, которые принадлежат одной прямой или лежат на параллельных прямых. Имеющие одинаковое направление коллинеарные векторы называются параллельными или сонаправленными векторами, а имеющие противоположное направление коллинеарные векторы называются антипараллельными или противоположно направленными векторами. Если два коллинеарных вектора  параллельны, то они обозначаются 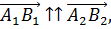а если антипараллельны, то они обозначаются  Все соответствующие координаты коллинеарных векторов пропорциональны.

Равные векторы – это параллельные (сонаправленные) векторы, которые имеют равные модули. Все соответствующие координаты равных векторов в заданной системе координат равны. Два равных вектора  обозначаются .

Противоположные векторы – это антипараллельные (противоположно направленные) векторы, которые имеют равные модули. Все соответствующие координаты равных векторов в заданной системе координат равны и имеют противоположные знаки. Два противоположных вектора  обозначаются .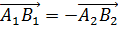

Сложение векторов – это линейная операция над векторами, результатом которой является вектор, проведённый из начала одного вектора в конец второго вектора при условии, что конец первого вектора совпадает с началом второго. Такой метод называется правилом треугольника сложения векторов. Координаты полученного вектора равны сумме соответствующих координат исходных векторов.

Вычитание векторов – это линейная операция над векторами, результатом которой является вектор, проведённый из конца вычитаемого вектора в конец уменьшаемого вектора при условии, что начала обоих векторов совпадают. Такой метод называется правилом треугольника вычитания векторов. Координаты полученного вектора равны разности соответствующих координат исходных векторов.

Умножение вектора на число – это линейная операция над вектором, результатом которой является вектор коллинеарный исходному вектору. Полученный вектор будет параллелен исходному вектору при умножении исходного вектора на положительное число, и полученный вектор будет антипараллелен исходному вектору при умножении исходного вектора на отрицательное число. Модуль полученного вектора при умножении исходного вектора на число k будет отличаться от исходного вектора в k раз. Координаты полученного вектора равны соответствующим координатам исходного вектора, умноженным на k.

Скалярное произведение векторов – это операция над векторами, результатом которой является число (скаляр), которое равно произведению модулей исходных векторов на косинус угла между этими векторами: 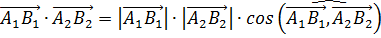. Скалярное произведение векторов численно равно сумме произведений соответствующих координат исходных векторов. Например, если вектор  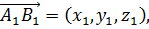а вектор  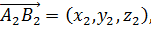то

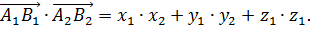
Векторное произведение векторов – это операция над векторами, результатом которой является вектор, модуль которого численно равен площади параллелограмма, построенного отложенными из общего начала исходными векторами. Длины сторон построенного параллелограмма равны модулям исходных векторов, а угол между сторонами параллелограмма равен углу между исходными векторами. Модуль полученного вектора численно равен произведению модулей исходных векторов на синус угла между этими векторами:  Полученный вектор будет перпендикулярен плоскости построенного параллелограмма и направлен так, что если смотреть с конца полученного вектора, то наименьшее вращение от вектора, являющегося первым сомножителем, к вектору, являющемуся вторым сомножителем, происходит против часовой стрелки. Векторное произведение векторов  и  обозначается  а координаты полученного вектора 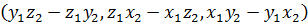.