 |
Алгебра. Геометрия
|
|
|
|
Алгебра
Алгебра – это раздел математики, предметом изучения которого являются величины, обозначенные цифрами и буквами, их отношения и свойства, независимо от их числового значения.
Возведение числа в степень – это одно из основных арифметических действий для числа. Возведение числа  в степень
в степень  обозначается
обозначается 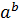 , где
, где  – это основание, а
– это основание, а  – это показатель степени.
– это показатель степени.
Возведение числа в степень с натуральным показателем – это одно из основных арифметических действий для числа. Возведение числа в степень с натуральным показателем осуществляется в результате последовательного многократного умножения основания степени на само себя в количестве раз равное показателю степени. Запись числа  в степени с натуральным показателем
в степени с натуральным показателем  :
:  , где
, где  – это основание степени, а
– это основание степени, а  – это показатель степени. Возведение числа в степень с натуральным показателем – это многократное умножение.
– это показатель степени. Возведение числа в степень с натуральным показателем – это многократное умножение.
Основные свойства возведения числа в степень с натуральным показателем:
· возведение в степень с натуральным показателем  произведения чисел равно произведению этих чисел, каждое из которых возведено в степень с натуральным показателем
произведения чисел равно произведению этих чисел, каждое из которых возведено в степень с натуральным показателем  :
:  ,
,
· возведение в степень с натуральным показателем  отношения чисел равно отношению этих чисел, каждое из которых возведено в степень с натуральным показателем
отношения чисел равно отношению этих чисел, каждое из которых возведено в степень с натуральным показателем  :
:  ,
,
· возведение числа в степень суммы натуральных показателей равно произведению этого числа на само себя, причём каждое из сомножителей возведено в степень с показателем равным каждому из слагаемых исходной суммы показателей степени:  ,
,
· возведение числа в степень разности натуральных показателей равно дроби, причём числитель дроби – это число, возведённое в степень равную уменьшаемому, а знаменатель дроби – это число, возведённое в степень равную вычитаемому исходной разности показателей степени: 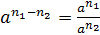 ,
,
|
|
|
· возведение числа в степень произведения натуральных показателей равно этому числу, последовательно возведённому в степень с показателем равным каждому из сомножителей исходного произведения показателей степени: 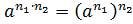 .
.
Возведение числа в степень с целым показателем – это одно из основных арифметических действий для числа. Запись числа в степени с целым показателем:  , где
, где  – это основание степени, а
– это основание степени, а  – это показатель степени. Возведённое в степень с целым положительным показателем число – это возведённое в степень с натуральным показателем число:
– это показатель степени. Возведённое в степень с целым положительным показателем число – это возведённое в степень с натуральным показателем число:  . Возведённое в нулевую степень ненулевое число равно единице:
. Возведённое в нулевую степень ненулевое число равно единице:  . Возведённое в степень с целым отрицательным показателем ненулевое число равно обратному числу, которое получено при возведении основания в модуль показателя степени:
. Возведённое в степень с целым отрицательным показателем ненулевое число равно обратному числу, которое получено при возведении основания в модуль показателя степени:  .
.
Корень из числа – это одно из основных арифметических действий для числа. Корень натуральной степени  из числа
из числа  обозначается
обозначается 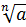 , где
, где  – это число (подкоренное выражение), а
– это число (подкоренное выражение), а  – это степень корня (показатель корня). Результатом извлечения корня натуральной степени
– это степень корня (показатель корня). Результатом извлечения корня натуральной степени  из числа
из числа  является такое число
является такое число  , которое при возведении его в степень равную показателю корня даёт исходное число (подкоренное выражение):
, которое при возведении его в степень равную показателю корня даёт исходное число (подкоренное выражение): 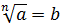 , где
, где  . Корень второй степени из числа обозначается только знаком радикала:
. Корень второй степени из числа обозначается только знаком радикала:  .
.
Основные свойства корня из числа:
· корень натуральной степени  из произведения чисел равен произведению корней натуральной степени
из произведения чисел равен произведению корней натуральной степени  из этих чисел:
из этих чисел: 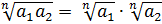 ,
,
· корень натуральной степени  из частного чисел равен отношению корней натуральной степени
из частного чисел равен отношению корней натуральной степени  из этих чисел:
из этих чисел:  , где
, где  - это ненулевое число.
- это ненулевое число.
Возведение числа в степень с рациональным показателем – это одно из основных арифметических действий для числа. Запись числа в степени с рациональным показателем:  , где
, где  – это основание степени, а
– это основание степени, а  – это показатель степени, причём
– это показатель степени, причём  – это целое число,
– это целое число,  – это натуральное число. Возведение числа
– это натуральное число. Возведение числа  в степень с рациональным показателем
в степень с рациональным показателем  можно заменить следующим образом:
можно заменить следующим образом:  .
.
|
|
|
Логарифм числа – это одно из основных арифметических действий для числа. Логарифм числа  по основанию
по основанию  обозначается
обозначается  , где
, где  – это положительное число,
– это положительное число,  – это основание логарифма, которое является положительным числом и не равно единице. Результатом логарифмирования числа
– это основание логарифма, которое является положительным числом и не равно единице. Результатом логарифмирования числа  является такое число
является такое число  , что при возведении основания логарифма
, что при возведении основания логарифма  в степень равную
в степень равную  получается исходное число
получается исходное число  :
:  , где
, где 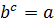 .
.
Основные свойства логарифма числа:
· результатом возведения числа 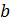 в степень с показателем равным логарифму числа
в степень с показателем равным логарифму числа  по основанию
по основанию 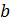 является число
является число  (основное логарифмическое тождество):
(основное логарифмическое тождество):  ,
,
· логарифм произведения двух чисел по основанию 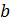 равен сумме логарифмов этих чисел по основанию
равен сумме логарифмов этих чисел по основанию 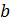 :
:  ,
,
· логарифм отношения двух чисел по основанию 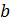 равен разности логарифмов этих чисел по основанию
равен разности логарифмов этих чисел по основанию 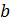 :
:  ,
,
· логарифм по основанию 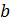 возведённого в степень числа равен произведению показателя степени и логарифма по основанию
возведённого в степень числа равен произведению показателя степени и логарифма по основанию 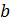 этого числа:
этого числа:  ,
,
· отношение двух логарифмов с равными основаниями равно логарифму числа равному числу логарифма числителя по основанию равному числу логарифма знаменателя:  .
.
Алгебраическое выражение – это выражение, в котором числа могут быть обозначены не только цифрами, но и буквами. Алгебраические величины, записанные цифрами и буквами, соединяются между собой знаками алгебраических действий и знаками последовательности этих действий.
Алгебраическая дробь – это дробь, числитель и знаменатель которой являются алгебраическими выражениями.
Переменная – это величина алгебраического выражения, записанная буквами.
Одночлен – это алгебраическое выражение, которое является произведением числа и одной или нескольких переменных, каждая из которых может быть возведена в степень. Степень одночлена равна сумме показателей степеней всех его переменных.
Многочлен – это сумма одночленов. Степень многочлена равна максимальной из степеней входящих в него одночленов.
|
|
|
Упрощение алгебраического выражения – это тождественное преобразование алгебраического выражения через последовательные алгебраические действия над многочленами алгебраического выражения, которые не нарушают смысла и истинности алгебраического выражения, а только позволяют представить исходное алгебраическое выражение в ином виде.
Разложение многочлена на множители – это тождественное преобразование многочлена через последовательные алгебраические действия над его одночленами, которые позволяют представить исходный многочлен в виде произведения нескольких сомножителей, каждый из которых является многочленом.
Формулы сокращённого умножения:
· разность квадратов двух чисел равна произведению разности этих чисел и их суммы:  ,
,
· квадрат суммы двух чисел равен сумме квадратов этих чисел и их удвоенному произведению: 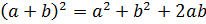 ,
,
· квадрат разности двух чисел равен разности суммы квадратов этих чисел и их удвоенного произведения: 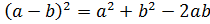 ,
,
· сумма кубов двух чисел равна произведению суммы этих чисел и неполного квадрата их разности:  ,
,
· разность кубов двух чисел равна произведению разности этих чисел и неполного квадрата их суммы:  .
.
Уравнение – это равенство двух многочленов, которые содержат одинаковые переменные. Переменные уравнения иначе называются неизвестные.
Решения уравнения – это все значения неизвестных, при которых уравнение является истинным. Решения уравнения иначе называются корни уравнения или аргументы функции. Решить уравнение – это значит найти все его корни или установить, что их нет.
Алгебраическое уравнение – это равенство многочлена нулю. Степень алгебраического уравнения равна степени многочлена.
Линейное уравнение – это алгебраическое уравнение, степень которого равна единице. Линейное уравнение с одной неизвестной имеет вид: 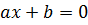 , линейное уравнение с двумя неизвестными имеет вид:
, линейное уравнение с двумя неизвестными имеет вид: 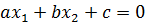 , где
, где  – это постоянные числа (коэффициенты), а
– это постоянные числа (коэффициенты), а 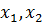 – это переменные.
– это переменные.
Квадратное уравнение – это алгебраическое уравнение, степень которого равна двум. Квадратное уравнение с одной неизвестной имеет вид:  , где
, где  – это постоянные числа (коэффициенты), а
– это постоянные числа (коэффициенты), а  – это переменная. Многочлен
– это переменная. Многочлен 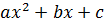 принято называть квадратный трёхчлен. Квадратное уравнение с одной неизвестной в общем случае имеет два корня:
принято называть квадратный трёхчлен. Квадратное уравнение с одной неизвестной в общем случае имеет два корня: 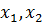 . Формула корней квадратного уравнения имеет вид:
. Формула корней квадратного уравнения имеет вид: 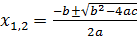 . Многочлен
. Многочлен  называется дискриминант и обозначается
называется дискриминант и обозначается 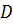 . Квадратное уравнение имеет корни при неотрицательном значении дискриминанта, а разложение квадратного трёхчлена на линейные множители имеет вид:
. Квадратное уравнение имеет корни при неотрицательном значении дискриминанта, а разложение квадратного трёхчлена на линейные множители имеет вид: 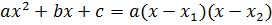 .
.
|
|
|
Теорема Виета (прямая): для квадратного уравнения  сумма корней
сумма корней  равна взятому с обратным знаком отношению коэффициентов
равна взятому с обратным знаком отношению коэффициентов  и
и  , а произведение корней квадратного уравнения равно отношению коэффициентов
, а произведение корней квадратного уравнения равно отношению коэффициентов  и
и 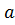 :
:  и
и 
Теорема Виета (обратная): два числа 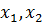 , которые удовлетворяют равенствам
, которые удовлетворяют равенствам  и
и  , являются корнями квадратного уравнения
, являются корнями квадратного уравнения 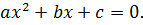
Система уравнений – это несколько уравнений, которые объединены общим решением.
Решение системы уравнений – это набор чисел, соответствующих значениям всех переменных уравнений системы и являющихся корнями для каждого уравнения системы.
Система двух линейных уравнений с двумя неизвестными – это система из двух алгебраических уравнений, каждое из которых является линейным уравнением вида 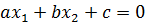 , где
, где  – это постоянные числа (коэффициенты), а
– это постоянные числа (коэффициенты), а 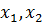 – это переменные. Система двух линейных уравнений с двумя неизвестными имеет вид:
– это переменные. Система двух линейных уравнений с двумя неизвестными имеет вид: 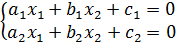
Неравенство – это соотношение между алгебраическими выражениями, которое показывает, что одно выражение больше или меньше другого или не равно другому. Неравенства записываются с помощью знаков: ≠ (не равно), < (меньше), > (больше), ≤ (меньше либо равно), ≥ (больше либо равно), < < (намного меньше), > > (намного больше).
Основные свойства уравнений и неравенств:
· к обеим частям уравнения или неравенства можно прибавить (вычесть) одно и то же алгебраическое выражение,
· любой одночлен уравнения или неравенства можно перенести из одной части в другую, при этом изменив знак этого одночлена на противоположный,
· обе части уравнения или неравенства можно умножить (разделить) на одно и то же положительное число,
· обе части уравнения или неравенства можно умножить (разделить) на одно и то же отрицательное число, при этом изменив знак неравенства на противоположный.
Прогрессия – это числовая последовательность, в которой каждая величина находится в определённой зависимости от предыдущей величины. Величины прогрессии называются члены прогрессии.
Арифметическая прогрессия – это числовая последовательность, в которой каждый член прогрессии, начиная со второго при условии ненулевого первого члена, больше предыдущего на величину  , причём
, причём  является постоянным числом и называется шаг или разность арифметической прогрессии. Если
является постоянным числом и называется шаг или разность арифметической прогрессии. Если  является положительным числом
является положительным числом 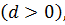 то арифметическая прогрессия называется возрастающей, если
то арифметическая прогрессия называется возрастающей, если  является отрицательным числом
является отрицательным числом 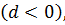 то арифметическая прогрессия называется убывающей, а если
то арифметическая прогрессия называется убывающей, а если  равно нулю
равно нулю 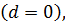 то арифметическая прогрессия называется стационарной. Формула n-го члена арифметической прогрессии
то арифметическая прогрессия называется стационарной. Формула n-го члена арифметической прогрессии  имеет вид:
имеет вид: 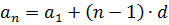 , где
, где 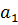 – это первый член арифметической прогрессии. Сумма арифметической прогрессии – это сумма всех n членов прогрессии
– это первый член арифметической прогрессии. Сумма арифметической прогрессии – это сумма всех n членов прогрессии  , которая в общем случае определяется соотношением:
, которая в общем случае определяется соотношением:  .
.
|
|
|
Геометрическая прогрессия – это числовая последовательность, в которой каждый член прогрессии, начиная со второго при условии ненулевого первого члена, больше предыдущего в  раз, причём
раз, причём  является ненулевым постоянным числом и называется знаменатель геометрической прогрессии. При условии положительного первого члена геометрической прогрессии, если
является ненулевым постоянным числом и называется знаменатель геометрической прогрессии. При условии положительного первого члена геометрической прогрессии, если  больше единицы
больше единицы 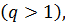 то геометрическая прогрессия называется возрастающей, если
то геометрическая прогрессия называется возрастающей, если  является числом большим нуля, но меньшим единицы
является числом большим нуля, но меньшим единицы  то геометрическая прогрессия называется убывающей, если
то геометрическая прогрессия называется убывающей, если  является отрицательным числом
является отрицательным числом  то геометрическая прогрессия называется знакочередующейся, а если
то геометрическая прогрессия называется знакочередующейся, а если  равно единице
равно единице 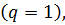 то геометрическая прогрессия называется стационарной. Формула n-го члена геометрической прогрессии
то геометрическая прогрессия называется стационарной. Формула n-го члена геометрической прогрессии  имеет вид:
имеет вид:  , где
, где  – это первый член геометрической прогрессии. Сумма геометрической прогрессии – это сумма всех n членов прогрессии
– это первый член геометрической прогрессии. Сумма геометрической прогрессии – это сумма всех n членов прогрессии  , которая в общем случае определяется соотношением:
, которая в общем случае определяется соотношением:  .
.
Функция – это установленное по определённому правилу однозначное соответствие между элементами двух числовых множеств, а значит, каждому элементу первого множества соответствует определённый элемент второго множества. Функцию можно задать несколькими способами, например, с помощью алгебраического уравнения (аналитический способ), графика (графический способ), таблицы значений (табличный способ).
Аналитический способ задания функции – это способ задания функции с помощью алгебраического уравнения в неявном виде  , где
, где  – это аргумент функции (переменная),
– это аргумент функции (переменная),  – это значение функции,
– это значение функции,  – это функция, то есть закон (правило), согласно которому каждому значению аргумента поставлено в соответствие определённое значение функции. Аналитический способ задания функции в явном виде имеет вид:
– это функция, то есть закон (правило), согласно которому каждому значению аргумента поставлено в соответствие определённое значение функции. Аналитический способ задания функции в явном виде имеет вид:  ), где
), где 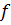 – это знак функции.
– это знак функции.
Область определения функции – это все допустимые значения аргумента функции, для которых функция определена.
Область значений функции – это все значения функции, которые она может принимать в области определения функции.
График функции – это геометрический образ функции в выбранной системе координат. Наиболее часто используется прямоугольная система координат, которая на плоскости называется декартовой системой координат.
Прямоугольная система координат – это система координат с взаимно перпендикулярными числовыми осями на плоскости или в пространстве, которые имеют общую точку начала отсчёта. Точка начала отсчёта определяет положительное и отрицательное направления числовых осей системы координат. Обычно оси системы координат носят названия  . Координаты любой точки A в прямоугольной системе координат однозначно определяются её тремя координатами:
. Координаты любой точки A в прямоугольной системе координат однозначно определяются её тремя координатами: 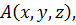 где x, y, z – это величины, которые с учётом знака численно равны наименьшим расстояниям от точки A до плоскостей, в которой лежат числовые оси
где x, y, z – это величины, которые с учётом знака численно равны наименьшим расстояниям от точки A до плоскостей, в которой лежат числовые оси  , соответственно.
, соответственно.
Декартова система координат – это прямоугольная система координат с равными единичными отрезками осей. На плоскости такая система координат задаётся двумя взаимно перпендикулярными числовыми осями, которые имеют общую точку начала отсчёта. Горизонтальная числовая ось называется абсцисса, и ей принадлежат значения аргумента функции x, а вертикальная числовая ось называется ордината, и ей принадлежат значения функции y.
График линейной функции – это график функции, которая в общем виде задаётся уравнением  , где x – это аргумент функции (переменная), y – это значение функции, a и b – это постоянные числа. График линейной функции называется прямая. Две прямые
, где x – это аргумент функции (переменная), y – это значение функции, a и b – это постоянные числа. График линейной функции называется прямая. Две прямые 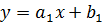 и
и  будут параллельными, то есть непересекающимися, при
будут параллельными, то есть непересекающимися, при  , и перпендикулярными, то есть образующими четыре угла по 90° при пересечении, при
, и перпендикулярными, то есть образующими четыре угла по 90° при пересечении, при  .
.
График квадратичной функции – это график функции, которая в общем виде задаётся уравнением 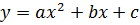 , где x – это аргумент функции (переменная), y – это значение функции, a – это постоянное ненулевое число, b и c – это постоянные числа. График квадратичной функции называется парабола.
, где x – это аргумент функции (переменная), y – это значение функции, a – это постоянное ненулевое число, b и c – это постоянные числа. График квадратичной функции называется парабола.
График степенной функции – это график функции, которая в общем виде задаётся уравнением  , где x – это аргумент функции (переменная), y – это значение функции, a – это постоянное число.
, где x – это аргумент функции (переменная), y – это значение функции, a – это постоянное число.
График показательной функции – это график функции, которая в общем виде задаётся уравнением 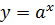 , где x – это аргумент функции (переменная), y – это значение функции, a – это постоянное неотрицательное число.
, где x – это аргумент функции (переменная), y – это значение функции, a – это постоянное неотрицательное число.
График логарифмической функции – это график функции, которая в общем виде задаётся уравнением 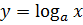 , где x – это аргумент функции (переменная), y – это значение функции, a – это постоянное неотрицательное число отличное от единицы.
, где x – это аргумент функции (переменная), y – это значение функции, a – это постоянное неотрицательное число отличное от единицы.
Геометрия
Геометрия – это раздел математики, предметом изучения которого являются различные пространственные формы (геометрические фигуры) и законы их измерения.
Плоская геометрическая фигура – это геометрическая фигура, все точки которой принадлежат одной плоскости.
Объёмная геометрическая фигура – это геометрическая фигура, не все точки которой принадлежат одной плоскости.
Луч – это часть прямой, которая состоит из точки прямой (начало луча) и всех точек прямой, лежащих по одну сторону от начала луча.
Отрезок – это часть прямой, которая состоит из двух различных точек прямой (концы отрезка) и всех точек прямой, лежащих между концами отрезка.
Угол – это плоская геометрическая фигура, которая образована двумя лучами, которые выходят из одной общей точки. Лучи в этом случае называются стороны угла, а их общая точка называется вершиной угла. Угол обозначается символом  и измеряется в радианах (рад) или градусах (°), причём острый угол меньше 90°, прямой угол равен 90°, а тупой угол больше 90°.
и измеряется в радианах (рад) или градусах (°), причём острый угол меньше 90°, прямой угол равен 90°, а тупой угол больше 90°.
Биссектриса угла – это луч, который выходит из вершины угла и делит этот угол на два равных угла.
Периметр плоской геометрической фигуры – это сумма длин всех сторон этой фигуры. Половина периметра плоской фигуры называется полупериметр. Периметр обозначается P и измеряется в единицах длины, то есть в метрах (м).
Площадь плоской геометрической фигуры – это численная характеристика плоской геометрической фигуры, которая описывает размер этой фигуры на плоскости. Площадь обозначается S и измеряется в квадратных метрах (м2).
Площадь объёмной геометрической фигуры – это численная характеристика объёмной геометрической фигуры, которая описывает размер поверхности этой фигуры. Площадь обозначается S и измеряется в квадратных метрах (м2).
Объём геометрической фигуры – это численная характеристика объёмной геометрической фигуры, которая описывает размер этой фигуры в пространстве. Объём обозначается V и измеряется в кубических метрах (м3).
Многоугольник – это плоская геометрическая фигура, которая образована n отрезками (стороны многоугольника), соединяющими n точек (вершины многоугольника), каждые три их которых не принадлежат одной прямой. Многоугольник лежит в одной плоскости. Выпуклый многоугольник – это многоугольник у которого любой угол меньше 180°. Сумма углов выпуклого n-угольника равна 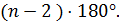
Окружность – это замкнутая кривая, которая состоит из всех точек, которые принадлежат одной плоскости и удалены от заданной точки (центр окружности) на равное расстояние. Отрезок, который соединяет центр окружности с любой точкой окружности, называется радиус окружности. Радиус окружности обозначается R. Периметр окружности L – это длина замкнутой кривой, которая определяется соотношением:  . Часть плоскости, которая находится внутри окружности, называется круг. Площадь круга S определяется соотношением:
. Часть плоскости, которая находится внутри окружности, называется круг. Площадь круга S определяется соотношением: 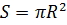 . Уравнение окружности в декартовой системе координат имеет вид:
. Уравнение окружности в декартовой системе координат имеет вид:  где
где  – это абсцисса и ордината центра окружности, соответственно.
– это абсцисса и ордината центра окружности, соответственно.
Вписанная окружность многоугольника – это окружность, которая лежит внутри многоугольника и касается каждой его стороны. Центр вписанной окружности находится в точке пересечения биссектрис углов многоугольника.
Описанная окружность многоугольника – это окружность, которая лежит вне многоугольника и содержит каждую его вершину. Центр описанной окружности находится в точке пересечения проведённых через середины сторон перпендикуляров к сторонам многоугольника.
Эллипс – это замкнутая кривая, которая состоит из всех точек, которые принадлежат одной плоскости, и для которых сумма расстояний до двух заданных точек (фокусы эллипса) одинакова и больше расстояния между этими двумя точками. Отрезок, который проходит через фокусы эллипса и концы которого принадлежат эллипсу, называется большой осью эллипса. Отрезок, который проходит через середину большой оси эллипса, перпендикулярен большой оси эллипса и концы которого принадлежат эллипсу, называется малой осью эллипса. Точка пересечения большой и малой осей эллипса называется центр эллипса. Отрезки, соединяющие центр эллипса с концами большой или малой осей эллипса, называются большой полуосью или малой полуосью эллипса, соответственно. Уравнение эллипса в декартовой системе координат имеет вид:  где
где  – это абсцисса и ордината центра эллипса, а
– это абсцисса и ордината центра эллипса, а  – это длины большой и малой полуосей эллипса, соответственно.
– это длины большой и малой полуосей эллипса, соответственно.
Треугольник – это плоская геометрическая фигура, которая образована тремя отрезками, соединяющими три точки, не принадлежащие одной прямой. Треугольник обозначается символом  Отрезки называются стороны треугольника, а точки называются вершины треугольника. Углы между отрезками называются углы треугольника. Прямоугольный треугольник имеет один прямой угол, тупоугольный треугольник имеет один тупой угол, остроугольный треугольник имеет все острые углы. Равносторонний треугольник имеет три стороны равной длины, равнобедренный треугольник имеет две стороны равной длины, разносторонний треугольник имеет все стороны разной длины.
Отрезки называются стороны треугольника, а точки называются вершины треугольника. Углы между отрезками называются углы треугольника. Прямоугольный треугольник имеет один прямой угол, тупоугольный треугольник имеет один тупой угол, остроугольный треугольник имеет все острые углы. Равносторонний треугольник имеет три стороны равной длины, равнобедренный треугольник имеет две стороны равной длины, разносторонний треугольник имеет все стороны разной длины.
Свойства треугольников:
· сумма всех углов треугольника равна 180°,
· сумма длин двух сторон треугольника больше длины третьей стороны.
Признаки равенства треугольников:
· две стороны и угол между этими сторонами одного треугольника равны двум сторонам и углу между ними другого треугольника,
· сторона и два прилежащих к этой стороне угла одного треугольника равны стороне и двум прилежащим к этой стороне углам другого треугольника,
· три стороны одного треугольника равны трём сторонам другого треугольника.
Подобные треугольники – это треугольники, у которых соответственно равны все углы, и все стороны одного треугольника пропорциональны лежащим напротив равных углов сторонам другого треугольника.
Признаки подобия треугольников:
· два угла одного треугольника соответственно равны двум углам другого треугольника,
· три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника,
· две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, и угол между этими сторонами одного треугольника равен углу между соответственно пропорциональными сторонами другого треугольника.
Медиана треугольника – это отрезок, который соединяет вершину треугольника с серединой лежащей напротив этой вершины стороны. Все медианы треугольника пересекаются в одной точке, которая называется центроид.
Биссектриса треугольника – это отрезок биссектрисы угла, который соединяет вершину треугольника с точкой лежащей напротив этой вершины стороны. Все биссектрисы треугольника пересекаются в одной точке, которая называется инцентр.
Высота треугольника – это отрезок, который проведён (опущен) из вершины треугольника к лежащей напротив этой вершины стороне так, что он перпендикулярен этой стороне или её продолжению. Все высоты треугольника пересекаются в одной точке, которая называется ортоцентр.
Площадь треугольника – это численная характеристика треугольника, которая определяется соотношением: 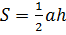 , где a – это длина любой стороны треугольника, а h – это длина высоты треугольника, которая опущена на сторону a.
, где a – это длина любой стороны треугольника, а h – это длина высоты треугольника, которая опущена на сторону a.
Вписанная окружность треугольника – это окружность, лежащая внутри треугольника и касающаяся трёх сторон треугольника. Треугольник в этом случае называется описанный треугольник.
Описанная окружность треугольника – это окружность, лежащая внутри треугольника и проходящая через три вершины треугольника. Треугольник в этом случае называется вписанный треугольник.
Четырёхугольник – это плоская геометрическая фигура, которая образована четырьмя отрезками, соединяющими четыре точки, никакие три из которых не принадлежат одной прямой. Отрезки называются стороны четырёхугольника, а точки называются вершины четырёхугольника. Углы между отрезками называются углы четырёхугольника.
Свойства треугольников:
· сумма всех углов выпуклого четырёхугольника равна 360°,
· сумма длин трёх сторон четырёхугольника больше длины четвёртой стороны.
Вписанная окружность четырёхугольника – это окружность, лежащая внутри четырёхугольника и касающаяся четырёх сторон треугольника. Четырёхугольник в этом случае называется описанный четырёхугольник.
Описанная окружность четырёхугольника – это окружность, лежащая внутри четырёхугольника и проходящая через четыре вершины четырёхугольника. Четырёхугольник в этом случае называется вписанный четырёхугольник.
Параллелограмм – это выпуклый четырёхугольник, у которого лежащие напротив друг друга (противоположные) стороны принадлежат параллельным прямым (параллельны). Площадь параллелограмма S определяется соотношением: 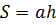 , где a – это длина любой стороны параллелограмма, а h – это длина высоты параллелограмма, которая опущена на сторону a.
, где a – это длина любой стороны параллелограмма, а h – это длина высоты параллелограмма, которая опущена на сторону a.
Прямоугольник – это параллелограмм, у которого все углы равны.
Ромб – это параллелограмм, у которого все стороны равны.
Квадрат – это ромб, у которого все углы равны.
Трапеция – это выпуклый четырёхугольник, у которого две противоположные стороны параллельны, и две другие противоположные стороны не параллельны. Параллельные противоположные стороны называются основания трапеции, а непараллельные противоположные стороны называются боковые стороны. Площадь трапеции S определяется соотношением: 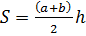 , где a, b – это длины оснований трапеции, а h – это длина высоты трапеции, которая опущена к любому основанию трапеции.
, где a, b – это длины оснований трапеции, а h – это длина высоты трапеции, которая опущена к любому основанию трапеции.
|
|
|


