График выполнения и сдачи заданий по дисциплине

 

№	Виды работ	Продолжительность выполне-ния	Форма контроля	Сроки сдачи	Баллы
Максимум	Штраф-ные
	Выполнение СРСП	1 неделя	Письменная ответ	По расписанию		за несвое-времен-ную сдачу
	Выполнение СРС	1неделя	Письменная ответ	По расписанию		за несвое-времен-ную сдачу
	Курсовая работа	13 недель	Письменная работа	14-15 неделя		за несвое-времен-ную сдачу

 

4. Карта учебно-методической обеспеченности дисциплины

Кафедра Математики тьютор Орлова Л.Г.

Дисциплина Теория и методика обучения математике в средней школе Количество кредитов _2__

№ п/ п	Наименование литературы	Наличие	Примечания
		В библиотеке	На кафедре	Обеспеченности студентов (%)	Электр онная версия
	Государственныеобщеобязательные стандарты среднего общего образования РК.			50%		В читал зале
	Начальное общее образование. -Алматы: РОНД, 2002 - с. 62-75			50%		В читал зале
	Государственные общеобязательные стандарты среднего общего образования РК.			30%		В читал зале
	Среднее общее образование. -Алматы:Программа. Математика (5-11классы) - Алматы: РОНД, 2003.			50%		В читал зале
	Абылкасымоыа А.Е. идр. Научно-методические основы совершенствования общего образования в Республике Казахстан. - Алматы, 2001.			50%		В читальном зале
	Абылкасымова А.Е., Уйгуров Е.А., омаров PC. Развитие системы общего среднего образования в современном мире:Учебное пособие. Алматы: НИЦ«Гылым», 2003			50%		В читальном зале
	Омаров Р.С., Кудайбердиев Т.К., Сариев А.А.. Особенности процесса обучения в условиях 12-летней школы: Методическое пособие - Алматы: НИЦ «Гылым», 2003.			50%		В читальном зале
	Онищук В.А. Урок в современной школе. -М.: 2005.			50%		В читальном зале
	Преемственность в обучении математике: Сборник статей // Сост. Пышкало A.M. - М.: Просвещение. 1978.			50%		В читальном зале
	Саранцев Г.И. Сборник упражнений по методике преподавания математике в средней школе.-М.: 1989.			50%		В читальном зале
	Самостоятельная деятельность учащихся при обучении математике. // Сост. СИ. Демидова, Л.О.Демидова. -М.: Просвещение, 1985			50%		В читальном зале
	Крутецкий В.А. Психология математических способностей школьников. - М. 1968.			50%		В читальном зале
	Лабораторные и практические работы по методике преподавания математики. // Под ред. Лещенко Е.И. - М.: 2004.			50%		В абонементе
	Метельский Н.В. Дидактика математики. Общая методика и её проблемы. Минск, БГУ, 1982.			50%		В читальном зале
	Методика преподавания математики в средней школе. // Сост. В.И. Мишин. - М. 1987.			50%		В читальном зале
	Методика преподавания математики в средней школе // Колягин М.Ю. в 2-х книгах.			50%		В читальном зале
	Проблемы методов обучения в современной общеобразовательной школе. -М. 2004.			50%		В читальном зале
	Рогановский Н.М. Методика преподавания математики в средней школе. - Минск, Высшая школа. 1990.			40%		В чит. зале

 

6. Лекционный комплекс:

Лекция № 1-2

Тема: Методика изучения числовых систем.

Содержание лекции:

1. Расширение понятия числа.

2. Изучение обыкновенных и десятичных дробей. Введение понятия доли и дроби.

3. Методика изучения действий над дробями.

4. Задачи на проценты.

Литература: [1-4],[7], [11-16], [18]

Понятие числа относится к основным понятиям математики. На вопрос «что такое число?»нельзя дать ответ, опираясь на ранее введение понятия.

Современная математика имеет дело с различными по природе числами: натуральные N, с целыми Z, рациональные 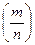Q, действительные числа R, иррациональные J, комплексные С, гиперкомплексные К.

Понятие числа возникло на заре человеческой цивилизации в результате деятельности человека. Постепенно происходило расширение понятия числа.

Nc Z c Q C R c C c r, каждое из этих множеств является расширением предыдущего, при этом имеется в виду, что множество У является расширением множества Х, если выполняются следующее условие:

Множество Х есть собственное подмножество множества У.

Все отношения и операции для элементов множества Х определены и в множестве У, при этом их смысл совпадает с тем, который они имели в Х до расширения.

В множестве У выполнена операция, которая в Х была не выполнима, или не всегда выполнима.

Расширение У является минимальным из всех возможных удовлетворяющим первым трем требованиям.

Первое расширение понятия числа происходит в 5-6 классах, к концу 6-го класса формулируется понятие рационального числа, дальнейшее расширение в 7-9 и далее в 10-11 классах, причем основные положения и представление о числе у учащихся сложились в 5-6 классах.

 

 

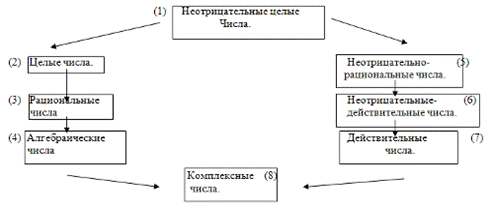
С точки зрения чистой алгебры естественный ряд обобщений идет по пути:

(1) (2) (3) (4) и на алгебраических числах заканчивается.

В школе рассмотрение понятия числа идет по пути (1) (5) (3) (7) (8)

При разработке программы для школы были предложения идти по пути (1) (2) (3), после того как ученики изучили целые числа должны перейти к понятию неотрицательного числа.

В начале 5-го класса ученики еще не готовы к введению понятия отрицательного числа, они не поймут почему из меньшего числа вычесть больше, а понятие дроби более естественно, оно связано с повседневной жизнью, поэтому выбором путь рассмотрения числа (1) (5) (3) (7) (8) от (7) (8) оставили на факультативные занятия.

А.А. Столяр предлагает показать учащимся, что расширение понятия числа происходит из потребности практики и в связи с этим предлагает следующую схему:

 

 

Введение дробных чисел возможно начиная с обыкновенных и десятичных дробей, необходимо исходит из начального освоения. Для первоначального усвоения обыкновенной дроби легче исходя из возраста их жизни, а затем десятичные.

Введение нового числа обычно опирается на жизненный опыт учащихся, необходима мотивировка, так введение дробных чисел связывает с измерением, делением на части, мотивировка может быть алгебраической, практической (вводятся индуктивным методом).

Методика введения новых чисел в школе.

Какие дроби изучали раньше обыкновенные или десятичные?

В большинстве случаев в школе принято изучать обыкновенные дроби, однако есть случаи когда первыми изучают десятичные дроби:

1) десятичные дроби имеют большую практическую ценность.

2) производить действия над десятичными дробями легче

3) теорию о десятичных дробях можно построить, используя понятие обыкновенной дроби, расширяя десятичную нумерацию меньшую единицы.

Доводы против-й стороны:

не следует отступать от исторического развития числа.

Не следует нарушать логику, обыкновенная дробь родовое понятие, а десятичная дробь- видовое, трудно обосновать действия над десятичными дробями без обыкновенной дроби.

Учащиеся не оценят легкость действий над десятичными дробями не познавая трудности при действии над обыкновенными.

Теоретическое значение обыкновенных дробей, выше вся алгебра построена на обыкновенных дробях.

Нумерация дробных чисел.

В нумерации натуральных и дробных чисел есть различия:

1. Натуральное число имеет единственное название и единственное обозначение.

Дробное число имеет бесконечное множество названий и обозначений.

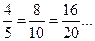
Обыкновенные дроби в отличии от десятичных читается неоднозначно.

При первоначальном введении новых понятий, надо начинать с небольшого 2-3х минутного исторического экскурса.

Источники получения дробных чисел.

1. Дробные числа появляются как результат измерения величин.

2. Разделение предметов на доли.

Дробные числа появляются в результате деления одного числа на другое.

Первоначальное ознакомление учащихся с дробью начинается в начальных классах, в 3 классе они знакомятся с долями, методикой ознакомления с простейшими дробями опора на конкретные образы долей величины, на практическое получение той или иной доли, а затем и дроби путем деления предметов, геометрических фигур на нужное число равных частей.

Нельзя допускать формального введения этих понятий.

В начальных классах для введения дроби учащиеся должны:

1) уметь называть и показывать доли со знаменателями не превышающие числа 10. Знать обиходное название этих дробей (половина, три, четверть).

2) уметь читать и записывать обыкновенные дроби со знаменателями не превышающие числа 10, показывать соответствующую дроби отрезка.

3) уметь сравнивать с опорой на рисунке указанные выше дроби, без опоры на рисунок уметь сравнивать дроби у которых числитель дроби =1.

4) уметь решать задачи на нахождение доли числа и числа по его долям, а также на нахождение дроби числа.

Каждый раз при решении таких задач используются рисунки, схемы, простые чертежи.

Изучение обыкновенных дробей начинается в 5 классе. В первом издании учебника математики 5- го класса уделялось мало времени на повторение материала 4- го класса.

Во втором издании этого учебника время на повторение увеличено, более обосновано излагается введение дробного числа.

Понятие дроби вводится в объеме достаточным для введения десятичных дробей. Здесь изучаются сведения о дробных числах, необходимых для систематического изучения дробей. Основное внимание уделяется сравнению дробей с одинаковыми знаменателями, а затем к выделению целой части числа. Необходимо чтоб учащиеся поняли, что дроби разные записи равных дробных чисел.

Желательно широко использовать различного рода наглядные пособия (бумажные ленты, метод демонстраций, линейки и др.), а также варьировать условие задачи.

Н-р: 1) как записать в виде дроби 3:4=3/4

2) на сколько нужно разделить 3, чтобы получить дробь ¾ (на 4).

При изучении дробных чисел учащиеся должны понять общий вид дробных чисел. Особое место занимает так называемое смешанные числа. Учащиеся должны понимать, что 2+ =2

Смешанное число термин школьный А.А. Колмогоров считает его неудачным и предлагает заменять термином смешанная дробь.

Рассмотрения действия над дробями при малейшем затруднении учащихся необходимо использовать наглядность. Это изображение дроби как части отрезка, прямоугольника, круга. Практика опытных учителей показывает, что следует четче различать отдельные случаи сложения и вычитания обыкновенных дробей с разными знаменателями.

Изучение этого материала лучше проходить в такой последовательности:

1) Сложение дробей, если знаменатель одной из дробей равен остальным.

2) Сложение дробей, если знаменатель одной прост, взаимно простые числа.

3) Приведение дробей к наименьшему общему знаменателю и сложение дробей

4) Примечание законов арифметических действий сложению дробей, содержащих целые и дробные части.

5) Вычитание положительных дробей.

6) Замена единицы дробью при вычитании.

7) Вычитание чисел содержащих целую и дробную часть.

8) Сложение и вычитание рациональных чисел.

Лекция №3-4

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: