 |
Тема: Виды вычислений и тождественных преобразований, методика их изучения
|
|
|
|
Содержание лекции:
1. Способы вычислений и тождественных преобразований и общие требования к ним.
2. Устные вычисления и тождественные преобразования. Письменные вычисления.
3. Тождественные преобразования в 7-8 классах
4. Особенности организации системы заданий при изучении тождественных преобразований
5. Доказательство тождеств
Литература: [1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4], II.
1. Определение: совокупность чисел и букв соединенных между собой по средствам знаком, которые указывают какие действия или в каком порядке надо произвести над данными числами и значениями букв называются английскими выражением.
Здесь к знакам отнесены (в 9 – летней школе) в основном изучается преобразование рациональных выражений, тождественных преобразований одночленов и многочленов, разложение на множители, преобразование алгебраических дробей.
 В погрому старших классов входит тождественное преобразование в тригонометрических и алгебраических выражений потенцированных (9 кл.)
В погрому старших классов входит тождественное преобразование в тригонометрических и алгебраических выражений потенцированных (9 кл.)
Таким образом, тождественные преобразования, как и другие основные вопросы школьного курса, не входят в одну какую нибудь тему, и рассматриваются во всем курсе алгебры.
2. Определение: Два алгебраических выражения называются тождественными, если они принимают равные численные значения при соответственно равных числовых значениях букв и С общей области допустимых значений.
Тождеством называется равенство двух тождественных выражений.
Для алгебраических дробей тождественность расширяется.
П. С. Александров, Калмагоров дают следующие определения. – Равенство между двумя рациональными выражениями будем называть тождественным, если оно справедливо при всех значениях входящих в него букв, кроме тех исключительных случаев, когда одна из сторон равенства (или он сразу) становятся бессмысленными.
|
|
|
Таким образом, в тождественных преобладаниях эта замена одного выражения другим тождественно равных. Смысл его сохраняется и для нового. Тождественные преобразования состоят в применение к данному выражению основных свойств к действию, необходимо обратить внимание на правильное оформление упражнений, на доказательство тождеств, запись может быть двоякой.
Если следует доказать,  , то
, то
1) 
2) 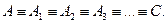

т.е. преобразовываем одну часть пока не получим другую или преобразовываем обе части пока не получим одно и тоже выражение в обеих частях.
Основную нагрузку по формированию умений и навыков выполнение преобразований несет курс алгебры.
На начальном этапе используется не расчлененная система преобразований.
П-р: Решить уравнение
а) 7х-5х=2
б) 7х=2+5х
в) 6+ (2-4у) +5у=3(1-3у)
при а) упрощение при помощи применения тождества (распределительным законом) т.е. (7-5)х=2
б) сводится к пункту а) по сред-вам равносильных преобразований путем переноса.
в) используется преобразование в первых двух случаев.
Принципиальное значение темы тождественное преобразование состоит в следующем:
Данное алгебраическое выражение преобразуется в более простое тождественное выражение.
Выполняя тождество ученики должны осознать, что эти преобразования не являются самоцелью, а служат для нахождения числовых значений выражений для решения уравнения, для изучения функции.
В начальном или 5 классе вводится понятие буквенного выражения. Выражения содержащие буквы называют буквенным выражением.
Для упрощения выражений используется распределительный закон умножения.
Тождественные выражения и их преобразования основываются на законах арифметических действий.
Н-р: 7*а*с*6=42ас
В 7 классе рассматриваются понятия одночлена, его стандартного вида, коэффициента одночлена, умножение одночленов, а также многочлен и его стандартный вид, сложения и вычитание многочленов, умножение многочлена на одночлен и приведение подобных членов.
|
|
|
При изучении этих тем особое внимание следует уделять оформлению записи в тетрадях.
Учащихся надо приучать записывать в порядке алфавита, это позволяет избежать ошибок, при приведении подобных слагаемых.
Н-р: Записи видо12у2х+3х2у+6ух2-3ху2=9ху2+9х2у=9(ху2+х2у)
При умножении многочлена на многочлен надо приучать учащихся строго соблюдать порядок умножения их членов. Н-р: каждый член первого многочлена последовательно умножать на каждый член другого многочлена, это на позволит пропустить некоторые члены многочлена или не повторить их дважды.
Тождества изучаемые в школе можно разделить на 2 класса; первый состоит из тождества сокращенного умножения, а второй обеими тождествами связывающие арифметические операции и основные элементарные функции.
Формулы сокращенного умножения рассматриваются в 7 классе, как частный случай умножения многочленов.
Рассматриваются формулы разность квадратов, квадрат суммы, квадрат разности, сумму и разность кубов.
Формулы куба разности и куба суммы двух выражений даются для учащихся в упражнениях.
К выводу формул умножения нужно привлекать самих учащихся.
Усвоению формул помогают такие предлагаемые упражнения, прочитать следующие выражения: а+с, а-с, (а+с)2, (а-с)2, ас, 2ас, и т.д.
Еще в процессе изучения темы умножения многочленов можно вывести формулу сокращенного умножения.
Так выполняя многократно умножения двух одинаковых многочленов, учащиеся замечают, какие члены получаются при умножении.
Постепенно можно отвлечься от подробной записи и сразу записать результат умножения, так можно поступать и с другими формулами.
Не следует торопить учащегося запоминать формулы, пусть они ещё раз умножат многочлены, при получении навыков тождественных преобразований учащийся можно выделить три основных этапа:
запоминание алгоритма и его применение.
Применение нового алгоритма к совокупности с ранее известными алгоритмами.
Решение широкого круга задач с использованием нового алгоритма.
|
|
|
Н-р: при изучении формулы разности квадратов рекомендуется выделять следующие этапы:
Применять его к упрощению выражение (с-3)(с+3), (5х+1)(5х-1) и т.д. Чтобы учащиеся поняли, что результат не зависит от порядка множителей и от порядка слагаемых в сумме.
Умение применять формулу (а-с)(а+с) в сочетании с другими тождественными преобразованиями, применением с использованием свойств степени с натуральными показателями.
П-р: (12с2-7а3)(7а3+12с2); (-11р4+9)(9+11р4)
Умение применять форму при решении уравнений, неравенств, и их систем при исследовании функции, задача на делимость и другие.
В этих этапах самым важным является первый этап, где учащимся раскрывается сущность нового алгоритма, создаются основы для его усвоения и правильного применения. Излишне поспешное беглое прохождение первого этапа является основной причиной грубых ошибок в преобразованиях допускаемые учащимися. К ним относятся, например, ошибки вида: 25*73=148
(а+2)2=а2+4
(х+1)2=х2+1
с целью предупреждения подобных ошибок необходимо время от времени предлагать учащимся называть определения свойств, на которые основано выполнение преобразования.
Н-р: если ученик записал (а4)2=а16, то надо не только вспомнить определение, но и сделать подробную запись.
(а4)2=а4а4=(а*а*а*а)(а*а*а*а)=а8
Иногда, чтобы убедить учащихся в ошибочной записи, необходимо использовать числовые подстановки.
Лекция №5-6
Тема: Изучение показательной и логарифмической функций
Содержание лекции:
1. Основные понятия
2. Изучение показательной функции
3. Изучение логарифмической функции
Литература: [1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4]. Учебники алгебры 10-11 класс
Анализ программы и методика. Функциональная пропедевтика в курсе математики. Изучение начинается в 7 классе, но подготовка намного раньше в начальных классах. Материал для этого дают по разделам связанным с зависимостью с различными арифметическим действиями и их комментариями. В 5 классе понятие единичного отрезка, координатной точки, координатного луча. Учащиеся встречаются с формулами при нахождении одной величины через любую другую. В 6 классе – координатная прямая и координатная плоскость. Умение отметить точку по заданным координатам, определить координаты точки. Умение читать (исследовать) графики и строить столбчатые диаграммы. В 7 классе тема функций является начальным этапом в подготовке учащихся. Рассматриваются примеры зависимости между двумя величинами (площадь квадрата и длина его стороны) такие зависимости одной от другой называют функциональными или функциями. Вводится понятие неизвестной переменной (аргумента), область определения значения функции зависящей переменной. Понятие графика функции. Способы задания функции (графический и табличный). Функциональные понятия получают конкретизацию при изучении линейных функций и прямой пропорциональности. Исследуется расположение графиков координатной плоскости от значений углового коэффициента, взаимное расположение графиков двух элементарных функций. Умения у учащихся находить значение функций по формуле, по известному значению аргумента, по графику и обратно. Все это делается на примерах. Тема «Степень с натуральным показателем», здесь рассматривается y=x2, у=х3. Формируются умения строить и читать график. 8 класс. Функция у=к/х и у=SQR (х) – зависимость с функцией у=х2, при х>=0. Решаются упражнения, где рассматриваются изменения функций у=|х| и ее графики. 9 класс. Изучается квадратичная функция ее свойства, график. У= ах2, у=ах2+вх+с которая получается из у=ах2 путем параллельного переноса все это объясняется на конкретных примерах. Внимание уделяется нахождению вершины параболы, оси симметрии, на направление ветвей. Умения находить промежутки возрастания убывания, промежутки, где функция сохраняет знак, схематическое построение графики, используя характерные точки, которые имеют существующее значение. Понятие функции – сложное математическое понятие, поэтому рассмотрение должно происходить на конкретных примерах. Функциональными понятиями овладевают при изучении элементарных функций (обратная и прямая пропорциональность, линейная функция, квадратичная функция, степенная). Рассмотрение этих функций происходит при изучении различных разделов алгебры, что позволяет изучать их в единстве с уравнениями. Характер изложения связан с возрастными особенностями учащихся и носит наглядно – индуктивный характер. Переход учащихся от геометрических представлений к аналитическому выражению свойств функции достаточно труден, следовательно. Прежде чем сформулировать возрастание и убывание рассматривают графики произвольных функций, вырабатывают индуктивное представление характера поведения функции на различных отрезках. Необходимо, чтобы была установлена связь между записями свойств функции в аналитической форме их геометрическим представлением. Изучение свойств подчиняется следующей схеме: 1. Рассмотрение конкретных ситуаций, которые приводят к выделению данной функции. 2. Сформулировать определение функции. Исследование входящих параметров. 3. Построение графика функций с помощью учащихся. 4. По графику прочитать основные свойства. 5. Использование изученных свойств при решении различных задач, в частности уравнений и неравенств.
|
|
|
|
|
|
Лекция №7-8
Тема: Уравнения и неравенства в школьном курсе математики
Содержание лекции:
1. Изучение уравнений и неравенств в 5-6 классах
2. Изучение линейных уравнений и неравенств в 6 классе
3. Решение текстовых задач с помощью линейных уравнений
Литература: [1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4], V,VI.
Лекция №9-10
Тема: Иррациональные уравнения и нерав-ва в курсе математики СШ
Содержание лекции
1. Изучение функции Öх
2. Преобразование иррациональных выражений
3. Решение иррациональных уравнений и неравенств и их систем
Литература:[1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4],
Решение уравнений составляет алгебраическую часть школьного курса. Задачи и методы алгебры возникли в результате поисков общих приемов для решения однотипных арифметических задач, эти приемы заключались в составлении и решении уравнений поэтому алгебра долгое время воспринималась как наука об уравнениях, сюда же привлекали и тождественные преобразования, которые подчинялись цели решения уравнений. В учебно-методической литературе уравнение рассматривается как аналитическая запись задачи об отыскании совокупности тех значений переменных при которых выражения в левой и правой части принимают равные значения. Согласно этому уравнение – это не само равенство, а лишь вопрос о $-и значений неизвестных, при которых имеет место равенство, при этом отождествляются понятия: уравнение, решить уравнение. Тем не менее термин уравнение часто употребляется вне связи с задачей отыскания его решения так например говорят о уравнении касательной, уравнении движения точки и т.п. Учащиеся начинают решать уравнения рано. В 1 кл. решают уравнения на основе правил нахождения неизвестного слагаемого, вычитаемого, уменьшаемого. Во 2 кл. – на основе правил нахождения неизвестного множителя, делимого, делителя. В 3 – 4 кл. умения закрепляются. В 5 кл. – уравнение определяется как равенство, содержащее неизвестные числа. Число при котором уравнение превращается в верное называется корнем уравнения. Решить уравнение – найти все его корни. В 6 кл. – возможность прибавить к обеим частям уравнения одно и то же число. Вводится перенос членов уравнения. В 7 кл. уравнение определяется как равенство содержащее переменную. Формулируется свойство равносильности. Решение линейного уравнения с параметрами. Понятие системы и рассматривается система линейных уравнений. Построение графика уравнения ax+by=c. В 8 кл. – квадратные уравнения. Решаются уравнения ax2+bx +c=0. решение дробно – рац. уравнений. В 9 кл. продолжается изучение уравнений и систем уравнений. Знакомятся с понятием степень целого рац. уравнения, что позволяет решать уравнения 3,4 степени. Система с двумя параметрами, графическое решение уравнений. Разработанный аппарат решения уравнений позволяет решать содержательные текстовые задачи методом уравнений. Программой предусматривается, чтобы в процессе обучения учащихся усвоили математические ЗиУ, усвоили важнейшие понятия курса, терминологию и язык, основ-е термины, формулы, правила, приемы и методы решения задач. Виды уравнений: линейные – ax+by=c, квадратные ax2+bx+c=0, дробно - рациональные, уравнение степени, логарифмические, показательные, тригонометрические. Методы решения: алгебраический (подстановка, замена, умножение на число), графический. Метод. замечания. 1. Понятие уравнений тесно связано с понятием корень уравнения, решить уравнение, система уравнений. Если уч-ся усваивают эти понятия, то => понимание теории и решения задач. Необходимо систематически разъяснять их смысл, приводя примеры. 2. При изучении уравнений уч-ся должны усвоить идею равносильности, использовать свойства равносильности уравнений и тождественных преобразований => рациональное решение уравнений. Целесообразно от уравнений с дробными коэффициентами перейти к уравнениям с целыми коэффициентами. 3. Необходимо обучить уч-ся алгоритмическим приемам. 4. Хорошим применением уравнений является текстовые задачи по алгебре. 5. для линии уравнений характерна направленность на установление связей с остальным содержанием курса математики тесно связано с числовой теорией, с функциональной линией, что служит наглядностью при решении уравнений. Без линии тождественных преобразований невозможно решение любого уравнения и их систем.
Неравенства
Можно выделить два основных пути развертывания содержания линии неравенств:
1) Сначала изучается материал относящийся к уравнениям и их системам, затем к неравенствам. Раздельное изложение проводится до теории квадратного трехчлена включительно. Дальнейшее изучение, происходящее в старших классах лишено этого противопоставления: логарифмические, показательные, тригонометрические уравнения и соответствующие неравенства изучаются в более тесной связи с друг другом.
2) Основные классы неравенств изучаются сразу вслед за изучением соответствующих классов уравнений. Имеются и промежуточные пути, когда некоторые классы уравнений и неравенств сближены друг другом по времени изучения, а другие наоборот не связаны.
С 1985-1990 года неравенства изучались с 4 класса. С 1990 года в соответствии с новой программой по математике теоретический материал о неравенствах дается в 8 классе. Особенности изучения неравенств: 1) как правило, навыки решения неравенств, за исключением квадратных формируются на более низком уровне, чем навыки решения уравнений соответствующих классов. Эта особенность имеет объективную природу: теория неравенств сложнее теории уравнений; 2) большинство приемов решения состоит в переходе от данного неравенства а>b, к уравнению a=b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства (исключение составляют линейные неравенства); 3) в изучении неравенств большую роль играют наглядно-графические средства.
8 класс. Учащие знакомятся с числовыми неравенствами, определением большего числа, свойствами числовых неравенств. Затем рассматриваются неравенства с одной переменной, понятие числового промежутка, система неравенств. Знакомство учащихся с неравенствами дает возможность использовать аппарат неравенств при решении самых разнообразных задач.
В неполной средней школе из неравенств содержащих переменную под знаком модуля рассматриваются неравенства вида |x-a|<b, |x-a|>b. Решение таких неравенств связывается в понятием расстояния между точками координатной прямой. Например: пусть требуется решить неравенство |x-1|<5, т.к. под модулем |х-1| выражает расстояние между точками координатной прямой, координаты которых равны х и 1, то надо найти множество координат точек удаленных от точки с координатой 1 меньше, чем на 5 единиц. Т.е |x-1|<5 равносильно -5<x-1<5 => -4<x<6.
Метод интервалов.
1. Исходное неравенство приводится к виду р(х)/q(x)>0, где p(x) и g (x) многочлены
2. Разложить многочлен p(x) и g(x) на множители 
3. Находим нули числителя и знаменателя
4. Если в разложении есть степень, то  нечетная степень заменяется первой степенью, четная степень опускается, но учитывается частное решение.
нечетная степень заменяется первой степенью, четная степень опускается, но учитывается частное решение.
5. Нули числителя и знаменателя отмечают на числовой прямой
6. Проводят кривую знаков.
Лекция №11-12
Тема: Изучение тригонометрических уравнений и неравенств
Содержание лекции:
1. Простейшие тригонометрические уравнения и неравенства
2. Различные типы тригонометрических уравнений
Литература: [1-4],[7], [11-16], [18]. Дополнительная литература I.[1-4], II, учебники и учебные пособия для учителя по алгебре 9-11 классов
|
|
|


