 |
Группы.Простейшие св-ва групп(с док-ми)
|
|
|
|
ОТНОШЕНИЕ ДЕЛИМОСТИ НА МН-ВЕ ЦЕЛЫХ ЧИСЕЛ, СВ-ВА ОТНОШЕНИЯ ДЕЛИМОСТИ.
Опр. Пусть a,b ∈ Z, а⋮b (а делится на b) или b/a, если (∃с ∈ Z): a=b*c, где a-кратное b, b-делитель a.
Св-ва отношения делимости:
(1)a⋮±a; a⋮±1;(2)a⋮b, b⋮c => a⋮c;
(3) a⋮b, b⋮c => (при любых m,n ∈ Z): am+bn⋮c;
(4) a⋮b, с⋮d => ac⋮bd;(5)ac⋮bc, c≠0 => a⋮b
(6)0⋮a
a⋮0 => a=0
a⋮b, a≠0 => b≠0;
(7)a⋮b, a∈N => a>=b;(8) a⋮b, b⋮a ó a=b или a=-b
Док-во:
(1)a=a*1=(-a)*(-1)
(2)a=bu, u∈ Z, b=cv, v∈ Z => a=cvu, т.к. uv ∈ Z, то a⋮c.
(6)0=а*0
a⋮0 => a=0*u, u∈ Z => a=0
a⋮b => a=bu, u∈ Z => если b=0, то а=0 –W => b≠0;
(7) a⋮b, а ∈N => b≠0 =>
b<0 => b<0<a => a>b
или b>0 => a=bu, u∈ Z => u>0 => u≥1 => bu≥b => a≥b;
(8) (<=) следует из п.1
(=>) a=bu, u∈ Z, b=av, v∈ Z => a=avu
a=0 =>b=0 или
a≠0 => ua=1 => u=v=1 или v=u=-1 => a=b или a=-b.
Деление с остатком. Теорема о делении с остатком.
Теорема:(a,b∈Z, b≠0)(! q,r∈Z): a=bq+r, 0≤r<|b|. (q-неполное частное, r-остаток)
Док-во:( ∃ )
(1)b>0=> (из аксиом)(q∈Z) bq≤a<b(q+1) => 0≤a-bq<b(q+1)-bq=b=|b|. (a-bq) обозначим r => a=bq+r.
(2)b<0=> -b>0=> (по пункту (1)) (q, r∈Z): a=(-b)q+r, 0≤r<|-b|=> a=b(-q)+r=bq′+r, 0≤r<|b|.(-q= q′)
(!) Пусть a=bq1+r1= bq2+r2, 0≤r1,r2<|b|=> b(q1-q2)=(r2-r1) => |b(q1-q2)=r2-r1| => |b||q1-q2|=|r2-r1|, 0≤|r2-r1|<|b| => 0≤|b||q1-q2|<|b| => 0≤|q1-q2|<1. Т.к. |q1-q2|∈Z => |q1-q2|=0 => q1-q2=0 => q1=q2 => r1=r2.
9*Простые числа.Основная теорема арифметики.Каноническое разложение на простые.Формула наибольшего общего делителя двух целых чисел.
Опр. Натуральное число,больше 1 н-ся простым,если оно не имеет других натуральных делителей,кроме 1 и себя самого.
1 не являестя ни простым,ни составным
Для (∀а∈Z)(∀ простое число р)
а делится на p => НОД (а,р)=р
а не делится на р=>НОД (а,р)=1
|
|
|
Теорема: (основная теорема арифметики)
Всякое целое число больше 1,разлагается в произведении простых чисел,при этом единственным с точностью до перестановки множителей образом.
Пример: 6=2*3=3*2 12=2*2*3=2*3*2=3*2*2
Опр n∈Z, а<1
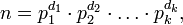где 
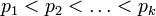— простые числа, и 
— некоторые натуральные числа.
Такое представление числа 
называется его каноническим разложением на простые сомножители.
Формула
Н.О.Д.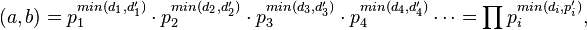 
Сравнение по модулю n. Свойства отношения сравнимости.
Опр. a,bϵz, nϵN. Говорят,что а≡b (mod n) (a сравнимо с n по mod n) или ф*b⁞n
Предлож. J nϵN
1)Отнош. срав-ти по модулю n есть отнош. эквивал-ти.
2) (∀a,b,c,dϵZ) a≡b (mod n), c≡d(mod n) ⇒a+c≡b+d(mod n), ac≡bd(mod n)
Док-во. ( 1) рефлексивность a≡a(mod n), т.к. а*а=0⁞n
симметричность а≡b(mod n)⇒a*b⁞n⇒ -(a-b)⁞n ⇒ b-a⁞n⇒ b≡a (mod n)
транзитивность a≡b (mod n), b≡с (mod n) ⇒ a-b⁞n; b-c⁞n⇒a-b+b-c⁞n↔a≡с (mod n)
(2) a≡b (mod n); c≡в (mod n)⇒a-b⁞n; c-d⁞n ⇒(a) a-b+c-d⁞n ⇒(a+c)-(b+d)⁞n⇒a+c≡b+в (mod n)
(б) (a-b)*c⁞n; (c-d)*b⁞n ⇒ac-bc⁞n; bc-bd⁞n ⇒ ac-bc+bc-bd⁞n⇒ac-bd⁞n⇒ac≡bd (mod n)
Предлож. J a,bϵZ, nϵN
a≡b (mod n) ↔ a и b имеют один. остаток при деление на n.
Док-во. ← ⇒ a*b=n(a1-a2)⁞n
→ r1-r2⁞n ⇒ǀr1-r2ǀ⁞n
Но 0≤ǀr1-r2ǀ<n ⇒ǀr1-r2ǀ=0 (т.к. если ǀr1-r2ǀ≠0, то ǀr1-r2ǀ≥n, т.к. ǀr1-r2ǀ⁞n) ⇒ r1-r2=0 ⇒ r1=r2
Сравнение по модулю n.Эквивалентные условия.Классы вычетов(кл.выч.), их кол-во. Операц-и на них, корректн-ть операц-й.
Опр. a,bϵz, nϵN. Говорят,что а≡b (mod n) (a сравнимо с n по mod n) или ф*b⁞n
ОПР: Классы эквивал.-ти по отношен. Сравн-ти по модулю n.наз-ся кл.выч.
ОБОЗН: a∈ℤ, n∈ ℕ
[a]=mod n={b∈ℤ, b≡a (mod n)}= ā
ℤ/≡mod n= ℤn–мн-во всех кл.выч. по mod n
ЗАМ: a,b∈ℤ, n∈ ℕ, ā= ó ab (mod n)
Следст.: имеется ровно n кл.выч по mod n, столько сколько ∃ остатков при делении на n.
ОПР: Опр-ые на ℤn операц. (∀a,b∈ℤ), положим ā +b(с чертой)=a+b(под одной чертой), a*b=a*b(аналогично)
|
|
|
Предл.: операц. на ℤn опр-ны корректно.
(b`=b c чертой)
Док-во: ā= ā1, b`=b`1 => a≡a1(modn); b≡b1(modn) => a+b≡a1+b1(modn)
ab=a1b1(modn) => a+b(общая черта)=а1+b1(о.ч); ab(о.ч)=a1b1(о.ч)
12!
Группы,абелевы гр.мульти-ая и аддит-ая
Форма записи.Примеры групп.
Опр. (группы)-непустое мн-во G с опред.на нем
Бинарной алгебраической операцией(умнож.)
Н-ся группой,если: (1 ) она ассоциативна:
(∀a,b,c∈G) (ab)c=a(bc)
(2) Имеет единицу: (∃е∈G)(∀a∈G) ae=ea=a
(3) Имеет обратную: (∀a∈G)(∃a¯¹∈G) aa¯¹=a¯¹a=e
Опр. (абелева гр)группа G н-ся коммутативной
или абелевой,если(∀a,b∈G) ab=ba
Зам. форма записи,при которой операция в гр.
Обозначается точкой,н-ся мультип-ой.Иногда
И только для абелевых гр.используется
Аддит-ая форма зап.
| Мулип-ая ф.з | Аддит-ая ф.з |
| Умножение (∙) | Сложение (+) |
| Единица (1,е) | Ноль (0) |
| Обратный (а¯¹) | Противополож.(-а) |
Примеры групп: ℕ∙ не явл.гр(нет обрат.у 2,3)
ℚ∙ не явл.гр.(нет обрат.у 0)
ℚ/{0}∙ абелева гр. ℤ+ абелева гр. ℤn+ абелева гр.
Группы.Простейшие св-ва групп(с док-ми)
Опр. (группы)-непустое мн-во G с опред.на нем
Бинарной алгебраической операцией(умнож.)
Н-ся группой,если: (1 ) она ассоциативна:
(∀a,b,c∈G) (ab)c=a(bc)
(2) Имеет единицу: (∃е∈G)(∀a∈G) ae=ea=a
(3) Имеет обратную: (∀a∈G)(∃a¯¹∈G) aa¯¹=a¯¹a=e
Простейшие свойства групп:
Пусть <G,∙>-группа
(1) е-единственна Д-во: Пусть е1,е2-единицы в G
е1=е1е2=е2(т.к е1 и е2 единицы) ч.т.д
(2) (∀а∈G)a¯¹ единственна Д-во: пусть а¯¹,а׳- обр.к а
а׳=ea׳=(a¯¹a)a׳=a¯¹(aa׳)=a¯¹e=a¯¹ ч.т.д.
(3) (∀a,b∈G)каждое ур-ее ax=b и ya=b имеет единств.
решение. Д-во: ax=b,возьмем х=а¯¹b⇒ax=a(a¯¹b)=
=(aa¯¹)b=eb=b⇒т.е х-решение
С др.стороны: Пусть ∃d∈G: ad=b⇒умнож.на а¯¹
а¯¹(ad)=a¯¹b=(a¯¹a)d=a¯¹b⇒ed=a¯¹b⇒d=a¯¹b
(ур-ее ya=b аналогич.(y=ba¯¹)
(4) св-во сокращения(∀a,b,c∈G) ab=ac⇒b=c
ba=ca⇒b=c Д-во: Пусть ab=ac⇒(умнож.на а¯¹сл.)
a¯¹(ab)=a¯¹(ac)⇒(a¯¹a)b=(a¯¹a)c⇒eb=ec⇒b=c
аналогич.ba=ca(умнож.на а¯¹сп)
(5) (∀a,b∈G) (ab)¯¹=b¯¹a¯¹ Д-во: ab(b¯¹a¯¹)=
((ab)b¯¹)a¯¹=(a(bb¯¹))a¯¹=(ae)a¯¹=aa¯¹=e ч.т.д.
|
|
|
Аналогично (b¯¹a¯¹)(ab)=e
15!
|
|
|
