 |
Определители матриц порядка 2 и 3.
|
|
|
|
Для квадратной матрицы вводится новое понятие - определитель матрицы. 
Определитель квадратной матрицы будем обозначать символом det A, и определим его индуктивным путем.
Определителем матрицы 2-го порядка
называется число, вычисленное по такому правилу: det A=a11a22-a12a21
Диагональ квадратной матрицы, которая идет от левого верхнего элемента таблицы до правого нижнего, называется главной диагональю матрицы. Диагональ, которая идет от правого верхнего элемента до левого нижнего, называется побочной диагональю матрицы.
Таким образом, для вычисления определителя матрицы 2-го порядка нужно из 
произведения элементов, которые находятся на главной диагонали матрицы,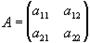 
вычесть произведение элементов, которые находятся на побочной диагонали.
Для определителя матрицы вводится символ
Таким образом,
(1)
Как видно из (1), определитель матрицы 2-го порядка представляет собой алгебраическую сумму двух слагаемых. Каждый из слагаемых является достижением двух элементов, при чем в него входит один элемент первой строки и один элемент 2-й строки, один элемент 1-го столбца и один элемент 2-го столбца заданной матрицы. Со знаком “+” берется произведение элементов главной диагонали и со знаком “-” - произведение элементов побочной диагонали.
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое 
входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.
|
|
|
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.
64.* Миноры и алгебраические дополнения. Теорема о разложении определителя по строке или столбцу. Определитель произведения.
Минором 
элемента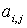 
матрицы n -го порядка называется определитель матрицы (n-1) -го порядка, полученный из матрицы А вычеркиванием i -й строки и j -го столбца.
При выписывании определителя (n-1) -го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.
Алгебраическим дополнением Аij элемента аij матрицы n -го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
.
Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
.
Теоремы о разложении определителя имеют важное значение в теоретических исследованиях. Они устанавливают, что проблема вычисления определителя n-го порядка сводится к проблеме вычисления n определителей (n –1)-го порядка.
Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть 
.
Если равны нулю все элементы какой-либо строки (столбца) матрицы 
за исключением быть может одного элемента, то определитель матрицы равен произведению этого элемента на его алгебраическое дополнение
|
|
|
65.* Миноры и алгебраические дополнения. Формула обратной матрицы. Правило Крамера решения систем линейных уравнений.
Миноры и алгебраические дополнения. Пусть F – поле скаляров и A = ||αik||∈Fmxn;
α11 · · · α1 n
A = · · · · · · ·
α m 1 · · · α mn
Определение. Определитель подматрицы k-го порядка матрицы A называется минором k-го порядка матрицы A. Минорами первого порядка матрицы A являются её элементы.
Определение. Определитель матрицы, полученной из квадратной матрицы A вычеркиванием i-й строки и k-го столбца, называется минором элемента α ik и обозначается через M ik. Произведение (-1) i+k M ik называется алгебраическим дополнением элементаα ik и обозначается через A ik.
Обратная матрица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E.
Правило Крамера решения систем линейных уравнений. Рассмотрим систему n линейных уравнений с n переменными:
α11x1+…+α1nxn= β1,
· · · · · · · · · · · · · · (1)
αn1x1+…+ αnnxn= βn
над полем F. Обозначим через A основную матрицу этой системы: A=||αik||.
Если |A| 
0, то система линейных уравнений (1) имеет единственное решение, выражаемое формулами:
X1=|A|-1(β1A11+…+ βnAn1), …
…, Xn= |A|-1(β1A1n+…+βnAnn).
66.* Свойства определителей.
Основные свойства определителей:
Свойство 1. Определители квадратной матрицы A и транспонированной матрицы tA равны.
Свойство 2. При перестановке двух столбцов (строк) матрицы её определитель меняет знак.
Свойство 3. Определитель матрицы, имеющий два одинаковых столбца (строки), равен нулю.
Свойство 4. Если все элементы какой-либо строки (столбца) матрицы А умножить на скаляр λ, то на скаляр λ умножится определитель матрицы A.
Свойство 5. Если каждый элемент i-й строки (столбца) квадратной матрицы A есть сумма m слагаемых, то определитель матрицы A равен сумме m определителей, причём в матрице первого определителя в i-й строке (i-м столбце) стоят первые слагаемые, в матрице второго – вторые и т.д., а остальные строки те же, что и в матрице A.
Свойство 6. Если к какому-нибудь столбцу (строке) матрицы определителя прибавить другой столбец (строку) матрицы, умноженный на произвольный скаляр, то определитель матрицы не изменится.
|
|
|
Свойство 7. Если какой-нибудь столбец (строка) квадратной матрицы есть линейная комбинация других столбцов (строк) матрицы, то определитель матрицы равен нулю.
|
|
|
