 |
Линейно зависимые и линейно независимые системы векторов. Примеры. Простейшие св-ва и признаки л.нез и л.зав систем векторов.
|
|
|
|
Пусть V – вектороное пространство над полем F. Система в-ов a1,…,аm пространства наз-ся линейно зависимой, если существуют скаляры λ1,…, λ∈F, не все равные нулю, такие, что λ1а1+…+ λm*am=0.
Система в-ов a1,…,аm пространства V наз-ся линейно независимой, если для любых скаляров λ1,…, λ∈F из равенства λ1а1+…+ λmam=0 следуют равенства λ1=0,…, λm=0.
Пример: R² ((0,0),(1,1)) л.з. α1(альфа)=1, α2=0. 1*V1+0*V2=(0,0)+(0,0)=(0,0)=0R²(в нижнем индексе)
Свойства и признаки:
1.(V) – л.з <=> V=0.
2.c-а, содержащая 0-й вектор л.з
3.с-а, -//- л.з подсистему л.з
4.(V1,…,Vm)-л.з <=> ∃i∈{1,…,m} Vi=л.комбин остальных векторов
5.Подсистема л.н с-мы л.н.
Док-ва: 1. (<=) V=0v. 1F(F-нижний индекс)*V=1F*0v
(=>) Пусть (V)-л.з. => (∃α∈F, α=0) α*V=0v => (∃α-¹∈F) α-¹(αV)= α-¹*0v => (α-¹ α)V=0v => V=0v
50. Основная лемма о линейной зависимости. Следствия основной леммы о линейной зависимости. Определение. Линейным пространством или векторным пространством 
над полем 
называется множествос двумя операциями: -- сложение 
, где 
;
-- умножение на скаляр 
, где 
,
для которых выполнены условия:
1) коммутативность сложения: x+y= y+x для любых 
,
2) ассоциативность сложения: для любых (x+y)+z=x+(y+z) 
,
3) существования нейтрального элемента 0: x+0=x для любого 
,
4) существования противоположного элемента - x: x+(-x)=0 для любого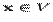 
,
5) 
для любых 
и 
,
6) 
для любого 
,
7) 
для любых 
и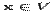 
,
8) 
для любых 
и 
.
Следствие. 1) Нейтральный элемент единственен.
2) Противоположный элемент единственен.
3) 0х= 0.
4) 
.. 5). 
6) 
тогда и только тогда, когда 
или x=0.
Определение. Пусть дана система векторов 
, где 
. Линейная комбинация векторов системы -- это выражение вида 
, где 
. Линейная комбинация 
называется тривиальной, если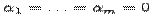 
. Система векторов 
называется линейно зависимой, если существует такая нетривиальная линейная комбинация 
, что 
. Система векторов 
называется линейно независимой, если из равенства 
следует, что 
.
|
|
|
Утверждение. [Свойства линейной зависимости] 1) Система (a), состоящая из одного вектора, линейно зависима тогда и только тогда, когда a=0.
2) Если m>1, то система линейно зависима тогда и только тогда, когда один из векторов системы линейно выражается через остальные.
3) Если подсистема 
системы 
линейно зависима, то и вся система линейно зависима.
4) Система, содержащая нулевой вектор, линейно зависима.
5) Если система линейно независима, а система 
линейно зависима, то вектор 
линейно выражается через вектора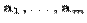 
.
Лемма. [Основная лемма о линейной зависимости и независимости системы] Пусть система векторов 
линейно независима, а каждый ее вектор линейно выражается через векторы системы 
. Тогда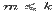 
.
Определение. Система 
называется максимальной линейно независимойсистемой в линейном пространстве , если любое расширение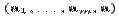 
этой системы линейно зависимо.
Следствие. Если и две максимальные линейно независимые системы в , то m=k.
Определение. Пространство называется 
-мерным (
), если в есть максимальная линейно независимая система, состоящая из векторов. Если такой подсистемы нет ни для какого 
, то 
. Если 
, то по определению 
Определение. Система векторов 
называется базисом линейного пространства , если каждый вектор 
единственным образом записывается в виде линейной комбинации 
, 
.
Предложение. Система векторов 
является базисом в пространстве тогда и только тогда, когда 
является максимальной линейно независимой системой в .
Предложение. Пусть -- -мерное векторное пространство, 
. Тогда в существует хотя бы один базис. Более того, каждая линейно независимая система 
может быть дополнена до некоторого базиса 
.
Предложение. Система 
является базисом в -мерном векторном пространстве тогда и только тогда, когда эта система линейно независима и 
.
|
|
|
Предложение. Система 
является базисом в -мерном векторном пространстве тогда и только тогда, когда и каждый вектор 
линейно выражается через эти векторы.
Рассмотрим арифметическое пространство 
, состоящее из множества строк 
, 
. Вектор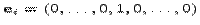а 
(на 
месте стоит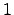 
) -- образуют базис.
Следствие. В пространстве система 
, 
, является базисом тогда и только тогда, когда
|
|
|
