 |
Неприводимые многочлены над полем действительных чисел
|
|
|
|
Неприводимый многочлен — многочлен, неразложимый на нетривиальные многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.
Неприводимый многочлен над полем 
― многочлен 
от 
переменных над полем является простым элементом кольца 
, то есть, непредставим в виде произведения 
, где 
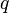и 
― многочлены с коэффициентами из , отличные от констант.
Многочлен f над полем F называется неприводимым (простым), если он имеет положительную степень и не имеет нетривиальных делителей (т.е., любой делитель либо ассоциирован с ним, либо с единицей)
Предложение 1
Пусть р – неприводимый и а – любой многочлен кольца F[x]. Тогда либо р делит а, либо р и а – взаимно простые.
Предложение 2
Пусть f ∈ F[x], и степень f = 1, значит, f – неприводимый многочлен.
Например: 1. Возьмем над полем Q многочлен х+1. Его степень равна 1, значит, он неприводим.
2. х2 +1 – неприводим, т.к. не имеет корней
СЛУ. Решение системы. Совместные, несовместные, определенные и неопределенные системы. Эквивалентные системы
Системой линейных уравнений над полем F с переменными х1,…хn называется система вида
а 11 х 1 + … + a 1n x n = b 1
………………………..
a m1 x 1 + … + a mn x n = b m
где a ik, b i ∈ F, m— количество уравнений, а n — количество неизвестных. Кратко эту систему можно записать так: ai1x1 + … + a in x n = b i (i = 1,…m.)
Эта СЛУ является условием с n свободными переменными х 1,….хn.
СЛУ делятся на несовместные (не имеют решений) и совместные (определенные и неопределенные). Совместная система вида называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой.
Например: над полем Q
|
|
|
х + у =1
х + у =2 - несовместная система
х + у = 1
х – у = 0 - совместная определенная (х, у = ½)
х + у = 1
2х + 2у = 2 - совместная неопределенная
Две системы л.у. являются эквивалентными, если множества решений этих систем совпадают, то есть, любое решение одной системы одновременно является решением другой. Систему, эквивалентную данной, можно получить:
1. заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число.
2. заменив одно из уравнений суммой этого уравнения с другим уравнением системы.
Решение СЛУ осуществляется методом Гаусса.
45* Элементарные преобразования систем линейных уравнений (слу). Метод Гаусса.
Опр. Элементарными преобразованиями С.Л.У н-ся следущие преобразования:
1. Умножения одного из системы уравнений системы на ненулевой элемент поля.
2. Прибавления к одному из уравнений системы другого уравнения, умноженного на элемент поля.
3. Добавления к системе или исключение из системы ненулевого уравнения 0*х1+0*х2+…+0*хn=0
4. Перемена местами уравнений
Предл. Пусть система (**)получена ил системы (*) с помощью конечного числа. Элемен-ых преобраз-ий. Тогда система (**)~ система(*). (Без док-ва)
Зам. При записи системы линейных уравнений будем использовать матричную запись.
а11 а12 … а1n в1
а21 а22 … а2n в2
………………….... …
Am1 am2... amn вn
Примеры: 1) 2х1 – х3 = 1 2 0 -1 1
х1 – х2 – х3 = 0 1 -1 -1 0
3х1 + 2х2 + 4х3 = 2 3 2 4 2
2) 1 0 1 х1=1
0 1 2 х2=2
3) 1 0 1 2 х1+х3=2 х1=2-х3
0 1 -1 3 х2-х3=3 х2=3+х3
Метод Гаусса
Предл. Пусть имеет система (*)
1. Все aij=0
(а) если все свободные члены равны 0 все вк=0 мн-во решений = Fn
(b) k вк=0 0х1+0х2+…+0хn= вк=0 (решений нет)
2. не все aij=0
(a)если в системе есть уравнение вид 0х1+0х2+…+0хn= вк=0 0
(b)если таких уравнений нет b1. Исключим ненулевые уравнения. Найдем самый маленький индекс i1, такой что не все коэф-ты при xij=0.
0……0……….. …. Второй столбец с нулями это i1.
0……0…..*=0….. ….
……….. …
0……0...……… …
|
|
|
1.перестановкой уравнений добьемся, чтобы a1i1 = 0
0 ….. 0… a1i1 = 0........ (1).:=(присваивание) (1) 1/ a1i1 (2).:=(2)-(1)* а2i1
............ a2i1............... 0…. 0…1…. …. 0…. 0..1….. ….. (ступенчатая
................................... 0…. 0… а2i1 … 0…..0..0… …. Матрица)
0........... 0.... ami1..... ……………… …. …………………… ….
0 ….0..аmi1... 0……0…………0 ….
Через конечное число шагов получим либо система содержит уравнение вида 0х1+0х2+…+0хn= вк=0 0либо
0……0 1………….. L1 “прямой ход Гаусса” 0....0 1...0..0.....0........0...... “обратный ход
0.......0 0......1..... L2 0....0 0.....1.........0.........0...... Гаусса”
0.......00........0....1 L2 0....0 0......0........1.........0......
................................................................................
0........0 0............0..1 Lk 0....0 0.......0.........0....0.......1..
(i1) (i2)
Переменные xi1,...... xik назовем главным, остальные свободными.
k=n => c-a определенная
k<n => c-a неопред-ая. Свободным переменным можно предавать производные значения, и вычислять значения главных переменных.
2 0 -1 1 8 (-3) 1 -1 -1 0 *(-2) 1 -1 -1 0
1 -1 -1 0 ~ 2 0 -1 1 ~ 0 2 1 1
3 2 4 2 3 2 4 2 0 5 7 2
46
|
|
|
