Область целостности, поля. Связь между полями и областями целостности.

Область целостности (или целостное кольцо, или область цельности или просто область) — понятие общей алгебры: ассоциативное коммутативное кольцо без делителя нуля (произведение ненулевых элементов не равно 0).

Эквивалентное определение: область целостности — это ассоциативное коммутативное кольцо, в котором нулевой идеал {0} является простым. Любая область целостности является подкольцом своего поля частных.

Поле в общей алгебре — множество F с двумя бинарными операциями 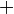(аддитивная операция, или сложение) и (мультипликативная операция, или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей , все ненулевые элементы которого обратимы.

Иными словами, множество F с двумя бинарными операциями 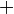(сложение) и (умножение) называется полем, если оно образует коммутативную группу по сложению , все его ненулевые элементы образуют коммутативную группу по умножению , и выполняется свойство дистрибутивности.

Теорема: Любое поле, а также любое кольцо с единицей, содержащееся в некотором поле, является областью целостности.

Обратно, любая область целостности может быть вложена в некоторое поле. Такое вложение дает конструкция поля частных.

Поле частных целостного кольца

Определение

Пусть 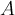— коммутативная область целостности. Положим .

Определение 1. Рассмотрим множество упорядоченных пар . Две упорядоченные пары и будем считать эквивалентными, если . Множество классов эквивалентности на обозначим через . Определим на операции сложения и умножения по правилу:

1. ,

2. ,

где обозначает класс эквивалентности элемента . Множество с указанными операциями будем называть полем отношений, или полем частных ¹⁾ кольца .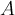

Предложение 1. Построенный в определении 1 объект является полем, нулевой элемент которого равен , а единичный — .

Пример 1. Поле рациональных чисел — это в точности поле частных кольца целых чисел .

 

 

23. Опр: кольцо, коммутативное и ассоциативное, с 1, F наз-ся полем, если |F|>1 и

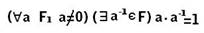. Опр: <F,+,*> - поле, P c F. Подмножество P наз-ся подполем поля F, если:

Обозн: P≤F Предлож: Пусть <F,+,*> - поле, P≤F.Тогда P само яв-ся полем относ-но оп-ции +, определённой на F.

Опр: Поля F и K называются изоморфными, если они изоморфны как кольца.

 

 

24. NcZcQcRcC, т.е. поле ком-ных ч-л вк-ет в себя все дейс-ные ч-ла.

Опр.: C = R x R (a_i,b_i)+(a_z,b_z)=^df (a_i+a_z; b_i+b_z); (a_i,b_i)+(a_z,b_z)=(a_ia_z-b_ib_z, a_ib_z-b_ia_z)

Предл: <C,+, *>- поле, т.е. C≠Ǿ +, * - бинарные ариф-ские оп-ции на С.

Замеч:

Опр: i=(0,1) – мнимая единица. Замеч: 1) i²=-1

2) (a,b)=(a,0)+(0,b)=(a,0)+(b,0)(0,1)=a+bi алгеб-ская

ф-ма записи ком-го ч-ла

z=a+bi, где a,b входят в R, a= Re z - реальное, b=In z – мнимое.

 

 

25.

26.

Формула Муавра:

 

Доказательство:

Лемма. Пусть , где.

Доказательство:

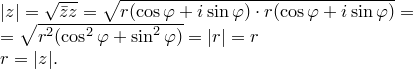
Пусть . Тогда . Но =>

Следовательно, числам и соответствует одна и та же точка числовой окружности. Значит, . Значит — одно из значений

 

Извлечение корней из комплексных чисел:

27. Кольцо многочленов от одной переменной:

Пусть K - поле. (здесь U(R) - группа обратимых элементов кольца R).

 

Доказательство. Если , то , т. е..

 

Если f(x) g(x)= 1, то , , 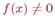и поэтому , т. е ,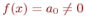

Не доделал(
у менят нет инфы о многочленах над областью целостности(((!!!!!

Теорема о делении с остатком в кольце многочленов под полем. Делении с остатком в кольце многочленов над областью целостности.

Теорема ]F-поле (например Q,R,C) Zp(р-простое)

(∀f,g∈F[x]g≠0)(∃!q,r∈F[x])

f=g*q+r; deg r<deg g

Замечание: Если К-о.ц.,но не поле,то утверждение,аналогичное теореме не выполняется.Однако:К-обалсть целостности

∀f,g∈K[x],g≠0,g=b_mx^m+...+b₀ и b_m-обратима в К

(∃!q,r∈К[x])f=gq+r;deg r<deg g

В формате ODT формулы выглядят по другом)Иероглифы это кваторы)

 

 

Значение многочлена и корень многочлена. Деление на многочлен (x-c). Теорема Безу.

Значение многочлена

Пусть 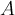— коммутативное ассоциативное кольцо с единицей, содержащееся в коммутативном целостном кольце 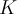, и — кольцо многочленов от одной переменной.

Предложение 1. Для каждого элемента существует единственный гомоморфизм колец такой, что

1. для всех ;

2. .

Определение 1. Результат применения отображения 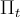к многочлену , то есть выражение , называется значением многочлена ¹⁾ при .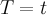

Пример 1. Пусть — многочлен над полем действительных чисел. Тогда его значение при — это .

Корень многочлена

Определение 2. Элемент 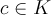называется корнем многочлена ²⁾ из кольца многочленов , если

.

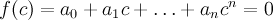Замечание 1. Операции сложения и умножения при вычислении выражения производятся в кольце .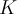

Пример 2. Рациональное число является корнем многочлена с целыми коэффициентами .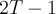

Пример 3. Мнимая единица является корнем многочлена .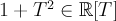

Теорема Безу

Теорема Безу утверждает, что остаток от деления многочлена 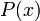на двучлен равен .

Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).

Доказательство

Поделим с остатком многочлен 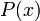на многочлен :

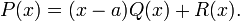
Так как , то — многочлен степени не выше 0. Подставляя , поскольку , имеем .

Следствия

• Число a является корнем многочлена 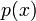тогда и только тогда, когда 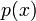делится без остатка на двучлен (отсюда, в частности, следует, что множество корней многочлена 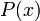тождественно множеству корней соответствующего уравнения ).
• Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
• Пусть α — целый корень приведённого многочлена A(x) с целыми коэффициентами. Тогда для любого целого k число A(k) делится на α-k.

·

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: