 |
Делимость, простые и неприводимые элементы
|
|
|
|
Пусть  и
и 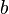 — элементы целостного кольца
— элементы целостного кольца  . Говорят, что «
. Говорят, что « делит
делит 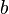 » или «
» или « — делитель
— делитель 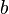 » (и пишут
» (и пишут  ), если и только если существует элемент
), если и только если существует элемент  такой, что
такой, что 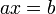 .
.
Делимость транзитивна: если  делит
делит 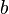 и
и 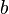 делит
делит  , то
, то  делит
делит  . Если
. Если  делит
делит 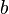 и
и  , то
, то  делит также их сумму
делит также их сумму  и разность
и разность  .
.
Для кольца  с единицей элементы
с единицей элементы  , которые делят 1, называются единицами или делителями единицы. Они и только они обратимы в
, которые делят 1, называются единицами или делителями единицы. Они и только они обратимы в  . Единицы делят все остальные элементы кольца.
. Единицы делят все остальные элементы кольца.
Элементы a и b называются ассоциированными, если a делит b и b делит a. a и b ассоциированны тогда и только тогда, когда  , где e — обратимый элемент.
, где e — обратимый элемент.
Ненулевой элемент 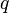 , не являющийся единицей называется неприводимым, если его нельзя разложить в произведение двух элементов, не являющихся единицами.
, не являющийся единицей называется неприводимым, если его нельзя разложить в произведение двух элементов, не являющихся единицами.
Ненулевой необратимый элемент 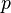 называется простым, если из того, что
называется простым, если из того, что 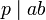 , следует
, следует 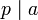 или
или  . Это определение обобщает понятие простого числа в кольце
. Это определение обобщает понятие простого числа в кольце  , однако учитывает и отрицательные простые числа. Если
, однако учитывает и отрицательные простые числа. Если 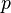 — простой элемент кольца, то порождаемый им главный идеал
— простой элемент кольца, то порождаемый им главный идеал  будет простым. Любой простой элемент неприводим, но обратное верно не во всех областях целостности.
будет простым. Любой простой элемент неприводим, но обратное верно не во всех областях целостности.
Свойства
- Любое поле, а также любое кольцо с единицей, содержащееся в некотором поле, является областью целостности.
- Обратно, любая область целостности может быть вложена в некоторое поле. Такое вложение дает конструкция поля частных.
- Если
 ― область целостности, то кольцо многочленов и кольцо формальных степенных рядов над
― область целостности, то кольцо многочленов и кольцо формальных степенных рядов над  также будут областями целостности.
также будут областями целостности. - Если
 ― коммутативное кольцо с единицей и
― коммутативное кольцо с единицей и  ― некоторый идеал в
― некоторый идеал в  , то кольцо
, то кольцо  является областью целостности тогда и только тогда, когда идеал
является областью целостности тогда и только тогда, когда идеал  прост.
прост. - Прямое произведение колец никогда не бывает областью целостности, так как единица первого кольца, умноженная на единицу второго кольца, даст 0.
- Тензорное произведение целостных колец тоже будет целостным кольцом.
- Характеристика области целостности является либо нулём, либо простым числом.
- Для любой области целостности существует поле частных.
Делитель нуля
|
|
|
В общей алгебре ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0.
Аналогично, ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0.
Элемент, который одновременно является и правым, и левым делителем нуля, называется делителем нуля. Если умножение в кольце коммутативно, то понятия правого и левого делителя совпадают. Ненулевой элемент кольца, который не являются ни правым, ни левым делителем нуля, называется обычным элементом.
Пример: в кольце  элементы 2, 3, 4 — делители нуля.
элементы 2, 3, 4 — делители нуля.
Ассоциативное коммутативное кольцо  без делителей нуля называется областью целостности.
без делителей нуля называется областью целостности.
Определение. Пусть А – произвольное кольцо, 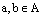 .
.
Если 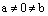 , но
, но  , тогда элемент а называют левым делителем нуля, а элемент b – правым делителем нуля. Если А – коммутативное кольцо, то элементы а и b называются делителями нуля.
, тогда элемент а называют левым делителем нуля, а элемент b – правым делителем нуля. Если А – коммутативное кольцо, то элементы а и b называются делителями нуля.
Определение. Если кольцо не имеет делителей нуля, то оно называется кольцом без делителей нуля.
Определение. Коммутативное кольцо с единицей и без делителей нуля называется областью целостности.
Пример 1. Кольцо целых чисел Z является областью целостности.
Пример 2. Кольцо многочленов над произвольным полем является областью целостности. (Смотри доказательство в Дополнение 2. Построение кольца многочленов.)
Пример 3. Кольцо функций  определенных на отрезке [0; 1] является коммутативным, с единицей, но с делителями нуля. Например, положим
определенных на отрезке [0; 1] является коммутативным, с единицей, но с делителями нуля. Например, положим
 ,
,  .
.
Тогда f(x) и g(x) – ненулевые функции, определенные на отрезке [0; 1], т.е. являются элементами кольца  , но их произведение, очевидно, равно нулевой функции:
, но их произведение, очевидно, равно нулевой функции:
|
|
|
 ,
,
где по определению полагают 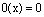 ,
,  и, очевидно,
и, очевидно, 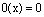 является нулем кольца.
является нулем кольца.
|
|
|


