 |
Количество корней многочлена над областью целостности.
|
|
|
|
Теорема 1. Кольцо многочленов над областью целостности само является областью целостности.
Данное нами алгебраическое определение многочлена не содержит никакого упоминания о функциях. Тем не менее, с каждым многочленом над областью целостности K можно естественным образом связать функцию, которая определена на K и принимает значения в K.
Пусть - многочлен с коэффициентами из K. Для любого положим
, (7)
где выражение в правой части понимается как результат операций в кольце K. Получаемый при этом элемент называется значением многочлена f (x) в точке x 0. (Слово "точка" употребляется по аналогии со случаем, когда x 0 можно представлять как точку действительной оси.) Таким образом, каждому элементу x 0 кольца K сопоставляется элемент f (x 0) того же кольца и тем самым определяется функция на K со значениями в K.
Покажем, что сложение и умножение многочленов согласуются с обычными операциями, производимыми над функциями, когда складываются или, соответственно, перемножаются значения функций в каждой точке.
Рассмотрим два многочлена:,. Пусть h (x) = f (x) + g (x) - их сумма. Докажем, что h (x 0)= = f (x 0) + g (x 0) для любого. В соответствии с формулой (1) =, где, что и требовалось доказать.
Пусть теперь - произведение многочленов f (x) и g (x). Докажем, что для любого. Перемножим равенства,. Пользуясь свойствами операций в кольце K (в частности, коммутативностью и ассоциативностью умножения), получим:, где. Сравнение полученного результата с формулой (2) позволяет сделать вывод, что.
Таким образом, функция, определяемая суммой (соответственно произведением) двух многочленов, есть сумма (соответственно произведение) функций, определяемых этими многочленами.
|
|
|
Вообще говоря, соответствие между многочленами и определяемыми ими функциями не является взаимно однозначным. Однако, если кольцо K бесконечно, то различным многочленам из кольца K [ x ] всегда соответствуют различные функции.
33-35!
36-37. НОД многочленов. Пусть F – поле. ] f,g ϵ F[x], f≠0 или g≠0. НОД f,g н-ся такой мн-тель d ϵ F[x], что: 1. d|f, d|g; 2. 
Запись: d=НОД(f,g) Положим, НОД (0,0)=0. Предл: Для любых f,g из F[x]: 1) Сущ. НОД (f,g) 2)НОД(f,g) определён однозначно с точностью до ассоциированности. Пример: d1=НОД(f,g); d1=d2 => d2=НОД(f,g) Об-чим с-лом d произ-ный НОД(f,g), тогда: 3)f≠0, g≠0 => d≠0; 4)(∃ u,v ϵ F[x]) fu+gv=d; 5)(∀đ ϵ F[x]) đ|f, đ|g=>đ|d; 6)(∀L, ß ϵ Fx) d=НОД(Lf, ßg)
Док-во: 1) ] f≠0 или g≠0. Считаем d≠0.Делим с остатком: f=g*q1+r1; deg r1< deg g; g=r1*q2+r2; deg r2< deg r1 => deg g> deg r1> deg r2>... Каждый элемент ≥0 или =-∞ Через ходы получаем остаток 0. Если есть остаток, то большее число заменяем на остаток от деления, т.е. используем алгоритм Евклида. rk-1=rk*qk+1+rk+1; rk=rk+1*qk+2+rk+2; rk+1=rk+2*qk+3+0; rk+2=НОД(f,g) a) rk+2|rk+1=>rk+2|rk=>…>rk+2|g=>rk+2|f в) ]đ<F[x], đ|f,đ|g=>đ|r1=>đ|r2=>…=>đ|rk+2=> т.е. rk+2≠0, то deg đ≤rk+2 2в) ]d1=НОД(f,d), d1~d2=>d2=L*d1, LϵFx Т.е. d1|d2; deg d1=deg d2 (deg d2=deg L(=0)+deg d1) 1)d1|f, d1|g=>d2|f,d2|g; 2)(∀đϵF[x]) đ|f, đ|g=>deg đ≤deg d1=deg d2, т.е. d2=НОД(f,g). Ос-е без д-ва
38!
Риводимые и неприводимые многочлены. Приводимость многочленов первой степени, многочленов, имеющих корень.
Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.
Приводимый многочлен — многочлен, разложимый на нетривиальные (неконстантные) многочлены. Приводимые многочлены не являются неприводимыми элементами кольца многочленов.
Определение
Неприводимый многочлен над полем  ― многочлен
― многочлен  от
от  переменных над полем
переменных над полем  является простым элементом кольца
является простым элементом кольца  , то есть, непредставим в виде произведения
, то есть, непредставим в виде произведения  , где
, где 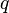 и
и  ― многочлены с коэффициентами из
― многочлены с коэффициентами из  , отличные от констант.
, отличные от констант.
|
|
|
Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида

абсолютно неприводим.
Корни неприводимого многочлена называются сопряженными.
Полином  , отличный от константы, называется неприводимым в
, отличный от константы, называется неприводимым в  если у
если у  нет нетривиального делителя в
нет нетривиального делителя в  . В противном случае
. В противном случае  называется приводимым в
называется приводимым в  .
.
Рассмотрим полином с рациональными коэффициентами:

Если полином  приводим в
приводим в  , то будет приводимым и полином
, то будет приводимым и полином  при
при 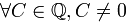 ; верно и обратное. Представив коэффициенты
; верно и обратное. Представив коэффициенты 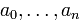 в виде несократимых дробей, возьмем
в виде несократимых дробей, возьмем
 знаменатель
знаменатель 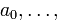 знаменатель
знаменатель 
(здесь  обозначает наименьшее общее кратное) тогда приводимость (или неприводимость) полинома
обозначает наименьшее общее кратное) тогда приводимость (или неприводимость) полинома  в
в  эквивалентна приводимости (соответственно, неприводимости) в
эквивалентна приводимости (соответственно, неприводимости) в  полинома
полинома  с целыми коэффициентами. Поэтому в дальнейшем будем сразу предполагать
с целыми коэффициентами. Поэтому в дальнейшем будем сразу предполагать  . Можно ли пойти дальше и утверждать, что приводимость такого полинома в
. Можно ли пойти дальше и утверждать, что приводимость такого полинома в  эквивалентна приводимости его в
эквивалентна приводимости его в  , т.е. полином раскладывается на произведение полиномов меньших степеней с рациональными коэффициентами тогда и только тогда, когда он раскладывается на произведение полиномов меньших степеней с целыми коэффициентами?
, т.е. полином раскладывается на произведение полиномов меньших степеней с рациональными коэффициентами тогда и только тогда, когда он раскладывается на произведение полиномов меньших степеней с целыми коэффициентами?
Теорема. Если полином

имеет рациональный корень, представленный в виде несократимой дроби  , то ее числитель
, то ее числитель  является делителем свободного члена
является делителем свободного члена 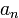 , а знаменатель
, а знаменатель  — делителем старшего коэффициента
— делителем старшего коэффициента  .
.
Доказательство. Условие  эквивалентно
эквивалентно

Это равенство можно переписать либо в виде
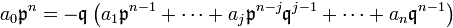
либо в виде

Из первого равенства следует, что  делится на
делится на  , а из второго — что
, а из второго — что 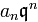 делится на
делится на  . Поскольку, по предположению теоремы, дробь
. Поскольку, по предположению теоремы, дробь 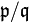 несократима, то
несократима, то  . Следовательно, число
. Следовательно, число  делится на
делится на  , a
, a 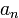 — на
— на  . ♦
. ♦
41-42
|
|
|


