 |
Сообщение темы и целей урока
|
|
|
|
Закрепление темы и целей урока
Задание 1 (с. 26) – по вариантам
Задание 2 (с. 26)
1) 20 + 25 = 45 (км) — весь путь;
2) 45: 9 = 5 (км/ч) — скорость;
3) 20 : 5 = 4 (ч) — время до привала;
4) 25 : 5 = 5 (ч) — время после привала
Задание 3 (с. 26)
Задание 7 (с. 27)
АВСD — квадрат.
Р = 16 см; Р = 4·а;
а = 4 см — сторона квадрата и ширина прямоугольника.
20 : 2 = 10 (см) — полупериметр прямоугольника.
10-4 = 6 (см) — длина прямоугольника.
Продолжим стороны АС и ВD квадрата на 2 см.
АВКЕ — прямоугольник.
Задание 8 (с. 27)
1545 м 1 км 894 м 5633 м
1 км 545 м 1894 м 5 км 633 м
Задание 11 (с. 27) – самостоятельно по вариантам
Подведение итогов урока
МАТЕМАТИКА
Тема: Окружность. Круг
Цели: познакомить учеников с окружностью; закрепить алгоритм умножения на однозначное число.
Организационный момент
Устный счёт
Вставь вместо * нужные цифры
| 13* | *4* | *0* | *14 |
| 3 | 3 | 4 | |
| *96 | 7*5 | 12*4 | 6*2 |
Сравните
1/3 от 300 см * 1 м
60 дм * 7 м
3 ч * 1/3 от 360 мин
50 мм * ½ дм
Задание 8 (с. 29)
Увеличить в 10 раз — умножить на 10.
30 дм 5 см • 10 = 305 см • 10 = 3050 см = 305 дм
50 кг 20 г • 10 = 50 020 г • 10 = 500 200 г = 500 кг 200 г
7 т 250 кг • 10 = 7250 кг • 10 = 72 500 кг = 72 т 500 кг
2 км 300 м • 10 = 2300 м • 10 = 23 000 м = 23 км
Решите задачи
• В 6 тетрадях 120 листов. Сколько листов в 9 таких тетрадях?
• Юннаты посадили 5 рядов анютиных глазок по 12 кустиков в каждом и 8 рядов по 20 кустиков в каждом. Сколько всего кустиков анютиных глазок посадили юннаты?
• Длина отрезка шелка 85 м. Продали 1/5 часть этого куска. Сколько метров материи осталось в куске?
• Площадь стола 4 800 см2, ширина — 60 см. Чему равен периметр стола?
• Ширина окна прямоугольной формы 4 дм, а длина — в 2 раза больше. Вычислите площадь окна.
Задание 3 (с. 28)
Ученики составляют задачу по рисунку: «Пешеход и велосипедист двигаются навстречу друг другу из пунктов А и В. Пешеход до встречи прошел с км, а велосипедист в 3 раза больше. Найти расстояние между пунктами А и Б».
|
|
|
В выражение с + с • 3 подставляются значения переменной:
2 + 2 • 3 = 8 (км);
3 + 3 • 3 = 12 (км);
5 + 5 • 3 = 20 (км).
Задание 5* (с. 29)
1) Нет. Ученики могут родиться в другие дни (по нескольку человек в день), но не 14 ноября.
2) Да. В году 12 месяцев. Если бы все ученики родились в разные месяцы, то их было бы не больше 12. Поскольку учеников 637, то хотя бы два из них родились в один и тот же месяц.
3) Да. В году 365 (366) дней. Если бы все ученики родились в разные дни, то их было бы не больше 365 (366). Поскольку учеников 637, то хотя бы два из них родились в один и тот же день.
Сообщение темы и целей урока
Объяснение нового материала
Задание 1 (с. 28)
Вывод: все радиусы одинаковой длины.
Задание 2 (с. 28) - устно
Точки А, В, D — принадлежат окружности и кругу;
точки А, В, D — принадлежат только окружности;
точки А, В, D, С, О — принадлежат кругу;
точка К — не принадлежит ни окружности, ни кругу.
Закрепление изученного материала
Задание 4 (с. 29) – самостоятельно по вариантам
| 24 030 |
Задание 6 (с. 28)
(80-20): 3 = 20 (л)
Задание 7 (с. 29)
х • 100 = 800
Подведение итогов урока
7. Домашнее задание: № 9, № 10, стр. 29
МАТЕМАТИКА
Тема: Нахождение чисел по сумме и разности
Цели: п ознакомить с приемом решения задач на нахождение чисел по их сумме и разности; закрепить алгоритм умножения на однозначное число.
Организационный момент
Устный счёт
Составьте выражение по схеме и найдите его значение
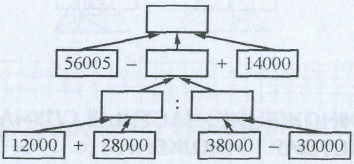
Задание 2 (с. 31)
Задание 4 (с. 31)
Неравенства решаются подбором или сведением к равенствам.
Например: 5 • а < 20; 5 • а = 20; а = 4.
Значит, а будет меньше 4: а = 0, 1, 2, 3 (проверяется).
Решите задачи
|
|
|
• У Игоря 1 600 марок. Он уже разложил по 80 марок в 5 альбомов. Сколько марок осталось разложить?
• 120 школьников поехали на экскурсию. В два больших автобуса сели по 50 человек. Остальные сели в два маленьких автобуса. Сколько человек ехало в маленьких автобусах?
• Яна купила 3 ручки по 900 рублей и тетрадей на 2 000 рублей. Сколько денег заплатила Яна?
• Велосипедист ехал 2 часа со скоростью 12 км/ч. После этого ему осталось проехать в 2 раза больше того, что он проехал. Сколько всего километров должен проехать велосипедист?
• Сравните площади квадрата со стороной 9 см и прямоугольника со сторонами 12 см и 8 см.
Задание 5* (с. 31)
Можно найти по отдельности сумму нечетных однозначных чисел, сумму четных и сравнить эти суммы:
1+3+5+7+9=25
2 + 4 + 6 + 8 = 20
25-20 = 5
Можно рассуждать по-другому. Каждое слагаемое второй суммы на 1 больше соответствующего слагаемого первой суммы. Сумма четырех слагаемых — больше на 4. Однако в первой сумме есть пятое слагаемое. Оно увеличивает первую сумму на 9. В результате первая сумма больше второй на 5. (9 - 4 = 5.)
Сообщение темы и целей урока
Объяснение нового материала
Задание 1 (с. 31)
Задача решается с опорой на рисунок.
Д. ___________________4___
М. __________________ 26
Какие числа нужно найти? (Количество мальчиков количество девочек.) Чему равна их сумма? (26.)
Разность? (4.) Каким образом можно сделать уравнивание этих чисел? (Ко второму числу прибавить 4 или из первого вычесть 4.) Как изменится при этом сумма? (Увеличится на 4 (26 + 4) или уменьшится на 4 (26-4).
Задача решается двумя способами.
Способ I.
1) 26 + 4 = 30 (ч.) — было бы в классе;
2) 30: 2 = 15 (ч.) — девочек;
3) 15 - 4 = 11 (ч.) или
26 - 15 = 11 (ч.) — мальчиков.
Способ II.
1) 26 – 4 = 22 (ч.) — было бы в классе;
2) 22: 2 = 11 (ч.) — мальчиков;
3) 11 + 4 = 15 (ч.) или
26 - 11 = 15 (ч.) — девочек.
|
|
|


